The algorithm is not the hard core "Nine Yang Sutra" in Jin Yong's martial arts novels, nor the lightweight "Lingbo micro step" ", which is the basic skill of programmers, just as people who practice martial arts need to take a horse step. Whether the Kung Fu is good or not depends on whether the horse step is not solid; whether the programming ability is strong or not depends on whether the algorithm ability is strong. This series adopts leetcode title number and JavaScript as the programming language. This article will gradually analyze the problem-solving ideas and finally give the code. On the one hand, this article records the author's problem-solving On the other hand, I hope I can communicate with you more and have a more efficient solution, or if there are any problems in the article, I hope you will give me your advice.

1, Topic: Rebuilding binary tree

Enter the results of preorder traversal and inorder traversal of a binary tree, please rebuild the binary tree. It is assumed that the input pre order traversal and middle order traversal results do not contain duplicate numbers.

For example, give

preorder = [3,9,20,15,7]
Middle order traversal inorder = [9,3,15,20,7]

Return the following binary tree:

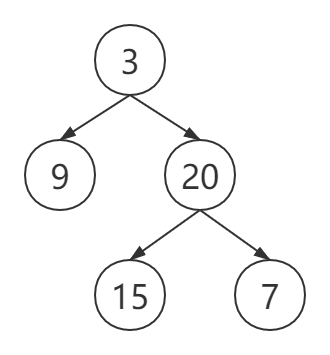
2, Little vest idea

In fact, the key to this problem is to understand what pre order and middle order traversal are and their traversal characteristics, so as to further analyze them. Now we know that the preorder traversal of binary tree is [3,9,20,15,7]. What conclusion can we draw? For preorder traversal, the root node must be the first element in the array.

It is known that the middle order traversal of binary tree is [9,3,15,20,7], and the corresponding root node of 3 is known from the previous order traversal. For the middle order traversal, the root node must be in the middle, that is, the left of the root node is the left subtree and the right of the root node is the right subtree.

According to the graph of middle order traversal, let's look again. The whole array represents a tree. There is a tree on the left of the root node and a tree on the right of the root node. This divides the big tree into small trees. Split the small trees in the same way until there is only one node left. Each time we process a tree, we generate a root node, recursively process its left and right trees, and assign them to the left and right attributes of the root node.

To sum up, there are four steps:

1. First, the root node is obtained and generated according to the pre order traversal
2. Secondly, according to the middle order traversal, the middle order left subtree and middle order right subtree are obtained
3. Thirdly, perform steps 1 and 2 recursively for the left and right subtrees until the number of subtrees is 1, and then directly return to the node
4. Finally, add the generated subtree to the original root node

3, Small vest solution

We know that the first element of preorder traversal must correspond to the root node, so it is also easy to generate the root node.

function TreeNode(key){
	this.key = key;
	this.left = this.right = null;
}

function buildTree(preorder, inorder){
	//if(preorder.length === 0){
	//	return null;
	//}

	let root = new TreeNode(preorder[0]);
}

When we know the value of the root node, we can get its position inRootPos in the middle order traversal array. The left side of the root node is the middle order left subtree, and the right side of the root node is the middle order right subtree. We can also get the front order left subtree and front order right subtree.

function buildTree(preorder, inorder){
	//if(preorder.length === 0){
	//	return null;
	//}

	//let root = new TreeNode(preorder[0]);
	let inRootPos = inorder.indexOf(root);
	// Left subtree preorder sequence
	let preorderLeft = preorder.slice(1, inRootPos + 1);
	// Ordered sequence in left subtree 
	let inorderLeft = inorder.slice(0, inRootPos);
	// Right subtree preorder sequence 
	let preorderRight = preorder.slice(inRootPos + 1);
	// Ordered sequence in right subtree
	let inorderRight = inorder.slice(inRootPos + 1);
}

Now we have the first and middle traversal sequence of the left and right subtrees. We can recursively process the left and right subtrees and set them as the left and right subtrees of the root node.

function buildTree(preorder, inorder){
	//if(preorder.length === 0){
	//	return null;
	//}

	//let root = new TreeNode(preorder[0]);
	//let inRootPos = inorder.indexOf(root);
	// Left subtree preorder sequence
	//let preorderLeft = preorder.slice(1, inRootPos + 1);
	// Ordered sequence in left subtree 
	//let inorderLeft = inorder.slice(0, inRootPos);
	// Right subtree preorder sequence 
	//let preorderRight = preorder.slice(inRootPos + 1);
	// Ordered sequence in right subtree
	//let inorderRight = inorder.slice(inRootPos + 1);

	root.left = buildTree(preorderLeft, inorderLeft);
	root.right = buildTree(preorderRight, inorderRight);

	return root;
}

This is our final code.

function TreeNode(key){
	this.key = key;
	this.left = this.right = null;
}

function buildTree(preorder, inorder){
	if(preorder.length === 0){
		return null;
	}

	let root = new TreeNode(preorder[0]);
	let inRootPos = inorder.indexOf(root);
	// Left subtree preorder sequence
	let preorderLeft = preorder.slice(1, inRootPos + 1);
	// Ordered sequence in left subtree 
	let inorderLeft = inorder.slice(0, inRootPos);
	// Right subtree preorder sequence 
	let preorderRight = preorder.slice(inRootPos + 1);
	// Ordered sequence in right subtree
	let inorderRight = inorder.slice(inRootPos + 1);

	root.left = buildTree(preorderLeft, inorderLeft);
	root.right = buildTree(preorderRight, inorderRight);

	return root;
}

4, Summary

This paper first analyzes the pre order traversal and middle order traversal of binary tree, and gives a four-step solution idea. Then the idea is gradually realized in code, the big problem is broken down, the left and right subtrees are processed recursively, and finally the JavaScript version of the algorithm program is obtained.

Basic knowledge Keywords: binary tree, tree traversal, recursion