
Small top pile
Other languages can complete the function of small top heap with priority queue, but JavaScript without built-in function needs to write a small top heap. Interview questions should be used. At least you can copy a correct data structure. If handwriting is required, we can also remember from understanding.
Previously written 23. Merge K ascending linked lists (difficult) JS codes
The small top heap (priority queue) has two main API s: insert to insert an element and delMin to delete the smallest element.
Binary heap can be realized by array. The core is that the parent node has a multiple relationship with the left and right child nodes. Build step by step
- Class data structure and access node (index) (be familiar with how JS writes classes)
class minHeap {
constructor(){
this.heap = []
}
getParent(index) {
return Math.trunc((index - 1) / 2)
}
getLeft(index) {
return index * 2 + 1
}
getRight(index) {
return index * 2 + 2
}
}
- Insert: add the element to be inserted to the end of the bottom of the heap (there is no place for you to insert), and then float it up (swim) to the correct position
- swim: if a node a is smaller than its parent node, a should not be a child node, but should replace the parent node and be the parent node by itself. This is the floating up of A. (the misplaced node a may have to float up many times to reach the correct position and restore the nature of the heap. Therefore, there must be a while loop in the code.)
swim(index) {
// Only one element
if(index == 0) return
// Cyclic adjustment
let parent = this.getParent(index)
while(this.heap[parent] && this.heap[parent] > this.heap[index]) {
this.swap(parent, index)
// The replaced parent node doesn't matter. The subtree with it as the root is still larger than the following nodes
index = parent
parent = this.getParent(index)
}
}
insert(value) {
this.heap.push(value)
this.swim(this.heap.length - 1)
}
- pop: to delete elements, first swap element A at the top of the heap with element B at the bottom of the heap, then delete A, and finally let B sink to the correct position.
- Sink: if A node A is larger than its child node (one of them), then A does not deserve to be the parent node. It should go down and the smaller node below should be the parent node. This is to sink A.
sink(index) {
// When sinking A node A, A needs to compare the size with its two child nodes
let left = this.getLeft(index)
while(left < this.heap.length) {
let right = this.getRight(index)
if(this.heap[right] && this.heap[right] < this.heap[left]) left = right
if(this.heap[left] < this.heap[index]) {
this.swap(left, index)
index = left
left = this.getLeft(index)
} else {
break // Both the left and right child nodes are larger than the parent node
}
}
}
pop(){
if(this.heap.length == 0) return undefined
if(this.heap.length == 1) return this.heap.shift()
let min = this.heap[0]
this.heap[0] = this.heap.pop()
this.sink(0)
return min
}
I found that the last time I learned from others is to use recursion to realize floating and sinking. This time, I use loop
Other functions
swap(p1, p2) {
[this.heap[p1], this.heap[p2]] = [this.heap[p2], this.heap[p1]]
}
peek() {
return this.heap[0]
}
size() {
return this.heap.length
}
215. The kth largest element in the array (medium)
Given the integer array nums and integer k, please return the K largest element in the array.
The biggest element of normal thinking must be the big top pile, but it can't be maintained after pop (see the next question). The small top heap does not need to build a heap of size N.

The code is simple. It mainly implements binary heap
var findKthLargest = function(nums, k) {
const proir = new MinHeap()
for(val of nums) {
proir.insert(val)
if(proir.size() > k) {
proir.pop()
}
}
return proir.heap[0]
};
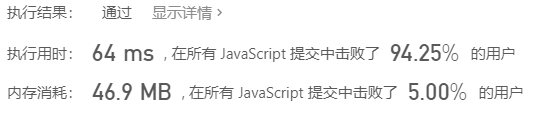
A small flaw was found in the code of the small top heap
295. Median data flow (difficult)
The median is the number in the middle of the sequence table. If the list length is even, the median is the average of the middle two numbers.
Design a data structure that supports the following two operations:
void addNum(int num) - adds an integer from the data stream to the data structure.
double findMedian() - returns the median of all current elements.
Refer to the article. If the data scale is very large, sorting is not realistic

The core idea of this question is to use two priority queues.
For a large top heap or small top heap, its median is in the middle layer of the binary tree.
Let the large top heap manage the small part, and the number of each time is the largest (low-level).
Let the small top stack manage the large part, and the number of each time is the smallest (high-level).
As long as the number of two heaps is the same, the top element of the heap is the median. The key is to keep the number of two heaps the same.
If you want to add elements to large, you can't add them directly, but first add them to small, and then add the small heap top elements to large; The same goes for adding elements to small.
Here, the small top pile or the large top pile is controlled by variables
var MedianFinder = function() {
this.minqueue = new PriorQueue('min') // High order number
this.maxqueue = new PriorQueue('max') // Low digit
};
/**
* @param {number} num
* @return {void}
*/
MedianFinder.prototype.addNum = function(num) {
// Priority number
if(this.minqueue.size() != this.maxqueue.size()) { // It indicates that the low number is small
this.minqueue.insert(num)
this.maxqueue.insert(this.minqueue.pop())
} else {
this.maxqueue.insert(num)
this.minqueue.insert(this.maxqueue.pop())
}
// console.log(this.minqueue.heap)
// console.log(this.maxqueue.heap)
};
/**
* @return {number}
*/
MedianFinder.prototype.findMedian = function() {
if(this.minqueue.size() == this.maxqueue.size()) {
return (this.minqueue.peek() + this.maxqueue.peek()) / 2
} else {
return this.minqueue.peek()
}
};
Problem: I thought the logic was wrong and made it for an hour.
I've been using this Heap [right] and this Heap [parent] to judge whether it is out of bounds. Unfortunately, it is not considered that the value of the element can be 0. There was no mistake before because the element is an object.
Be more rigorous, math TRUNC ((index - 1) / 2), because - 0.5 becomes 0
Should read
parent>=0 right<this.heap.length Math.floor((index-1)/2)
The final completely correct code of small top heap and large top heap
class PriorQueue {
constructor(mark) {
this.heap = []
this.mark = mark
}
getParent(index) {
return Math.floor((index-1)/2)
}
getLeft(index) {
return index * 2 + 1
}
getRight(index) {
return index * 2 + 2
}
compare(p, cur) {
if(this.mark=='min') {
return p > cur
} else {
return p < cur
}
}
swim(index) {
if(index==0) return
let parent = this.getParent(index)
while(parent>=0 && this.compare(this.heap[parent], this.heap[index])) {
this.swap(parent, index)
index = parent
parent = this.getParent(index)
}
}
insert(val) {
this.heap.push(val)
this.swim(this.heap.length-1)
}
sink(index) {
let left = this.getLeft(index)
while(left < this.heap.length) {
let right = this.getRight(index)
if(right<this.heap.length && this.compare(this.heap[left], this.heap[right])) left = right
if(this.compare(this.heap[index], this.heap[left])) {
this.swap(left, index)
index = left
left = this.getLeft(index)
} else {
break
}
}
}
pop() {
if(this.heap.length == 0) return undefined
if(this.heap.length == 1) return this.heap.shift()
let min = this.heap[0]
this.heap[0] = this.heap.pop()
this.sink(0)
return min
}
swap(p1, p2) {
[this.heap[p1], this.heap[p2]] = [this.heap[p2], this.heap[p1]]
}
peek() {
return this.heap[0]
}
size() {
return this.heap.length
}
}
703. The K-th element in the data stream (simple)
Design a class that finds the k-th largest element in the data flow. Note that it is the k-th largest element after sorting, not the k-th different element.

Because every time a number is added, the element with the largest K is returned, indicating that the largest K number is stored in the binary heap. Use a small top pile to maintain. Use the modified small top pile:
var KthLargest = function(k, nums) {
this.k = k
this.minqueue = new PriorQueue('min')
for (val of nums) this.minqueue.insert(val)
};
/**
* @param {number} val
* @return {number}
*/
KthLargest.prototype.add = function(val) {
this.minqueue.insert(val)
while(this.minqueue.size() > this.k) this.minqueue.pop()
return this.minqueue.peek()
};
Interval problem

There are two main techniques:

The idea of sorting: it is applied to the envelope nesting problem
1288. Delete the covered interval (medium) fail
Give you a list of intervals. Please delete the intervals covered by other intervals in the list.
Only when C < = A and B < = D, we think that interval [a,b) is covered by interval [c,d).
After all deletion operations are completed, please return to the number of remaining intervals in the list.

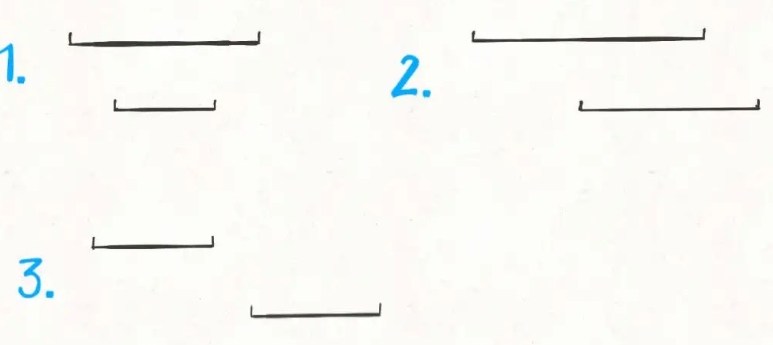

This paper lists three cases, but only two need to be considered in practice: coverage and non coverage.
Because the starting point is increasing, after considering the current element, the next one must start to the right. If not covered, what we need is a larger end point, and the starting point is just incidental.
var removeCoveredIntervals = function(intervals) {
intervals.sort((a, b) => {return a[0]==b[0] ? b[1]-a[1] : a[0] - b[0] })
let st = intervals[0][0], en = intervals[0][1], count = 0
for (let i = 1; i < intervals.length; i++) {
if(st <= intervals[i][0] && en >= intervals[i][1]) {
count++
} else {
st = intervals[i][0]
en = intervals[i][1]
}
}
return intervals.length - count;
};
Difficulty or: why should we arrange the end points in descending order
For these two intervals with the same starting point, we need to ensure that the long interval is above (in descending order of the end point), so that it can be determined that the first covers the second. Otherwise, it will be wrongly determined as intersection (not covered), and then update the end point
var removeCoveredIntervals = function(intervals) {
intervals.sort((a, b) => {return a[0]==b[0] ? b[1]-a[1] : a[0] - b[0] })
let en = intervals[0][1], count = 0
for (let i = 1; i < intervals.length; i++) {
if(en >= intervals[i][1]) {
count++
} else {
en = intervals[i][1]
}
}
return intervals.length - count;
};
56. Consolidation interval (medium)
An array of intervals is used to represent a set of several intervals, in which a single interval is intervals[i] = [starti, endi]. Please merge all overlapping intervals and return a non overlapping interval array, which needs to cover all the intervals in the input.

Sort operation
This question is about to consider the intersection.
var merge = function(intervals) {
intervals.sort((a, b) => {return a[0]==b[0] ? b[1]-a[1] : a[0]-b[0] })
let st = intervals[0][0], en = intervals[0][1], ans = []
for(let i=1; i<intervals.length; i++) {
// Contain
if(st<=intervals[i][0] && en>=intervals[i][1]) continue
// intersect
if(en>=intervals[i][0] && en<=intervals[i][1]) {
en = intervals[i][1]
}
// Disjoint
if(en < intervals[i][0]) {
ans.push([st, en])
st = intervals[i][0]
en = intervals[i][1]
}
}
// There's one group left
ans.push([st, en])
return ans;
};
The article only sorts the starting point here, because it combines the two cases of coverage and intersection.
Only overlap and disjoint. (EN > = intervals [i] [0] and en < intervals [i] [0])
57. Insert interval (medium) fail
Give you a non overlapping list of intervals sorted by the beginning and end of the interval.
To insert a new interval into the list, you need to ensure that the intervals in the list are still orderly and do not overlap (merge the intervals if necessary).

Compare each section with the new area
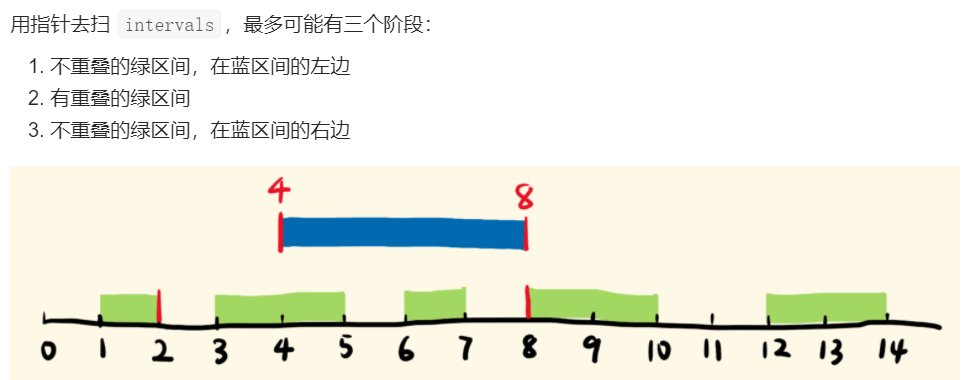
To be right, the key is to understand the conditions of green new areas from entering the blue range to coming out of the blue range. I only stare at the two ends of the blue range, and I don't have a concept of sliding.

var insert = function(intervals, newInterval) {
let res = [], i = 0, len = intervals.length
// Left side between new districts
while(i < len && intervals[i][1]<newInterval[0]) {
res.push(intervals[i])
i++
}
// Intersection or inclusion
while(i<len && intervals[i][0]<=newInterval[1]) {
newInterval[0] = Math.min(intervals[i][0], newInterval[0])
newInterval[1] = Math.max(intervals[i][1], newInterval[1])
i++
}
res.push(newInterval)
while(i<len) {
res.push(intervals[i])
i++
}
return res;
};
986. Intersection of interval lists (medium)
Although I have done it in the array, I obviously know what circumstances to consider. So do it again on your own.
The intersection of two closed intervals is a set of real numbers, either empty sets or closed intervals. For example, the intersection of [1,3] and [2,4] is [2,3].
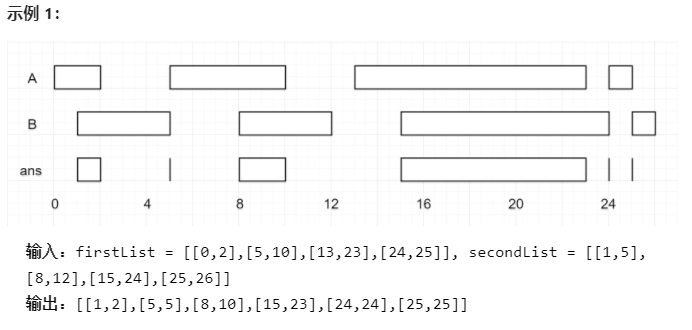
Intersection: 4 types
Disjoint: 2
After comparison, who moved? Look at the end. If you compare the previous one, you don't need it.
var intervalIntersection = function(firstList, secondList) {
let i = 0, j = 0, res = [];
while (i<firstList.length && j<secondList.length) {
let [a1, a2] = firstList[i], [b1, b2] = secondList[j]
// No intersection
if(a2 < b1 || a1 > b2) {
a2 < b2 ? i++ : j++
continue
}
// Have intersection
if(a2 >= b1 && a1 <= b2) {
res.push([Math.max(a1, b1), Math.min(a2, b2)])
}
// Keep further
a2 < b2 ? i++ : j++
}
return res
};
Interval scheduling problem (greedy algorithm)



435. Non overlapping interval (medium)
Given a set of intervals, where intervals[i] = [starti, endi]. Returns the minimum number of intervals to be removed so that the remaining intervals do not overlap each other.

At least a few intervals need to be removed? On the contrary, there are at most several disjoint intervals in the interval.
var eraseOverlapIntervals = function(intervals) {
if(intervals.length == 0) return 0
intervals.sort((a, b) => {return a[1] - b[1]})
let i = 1, end = intervals[0][1], count = 1
for(; i<intervals.length; i++) {
if(intervals[i][0] < end) continue
count++
end = intervals[i][1]
}
return intervals.length - count
};
452. Detonate the balloon with the minimum number of arrows (medium)
A bow and arrow can be shot completely vertically from different points along the x-axis. Shoot an arrow at the coordinate X. if the start and end coordinates of the diameter of a balloon are xstart, xend and xstart ≤ x ≤ xend, the balloon will be detonated. There is no limit to the number of bows and arrows you can shoot. Once a bow and arrow is shot, it can move forward indefinitely. We want to find the minimum number of bows and arrows needed to detonate all balloons.
Give you an array of points, where points [i] = [xstart,xend] returns the minimum number of bows and arrows that must be fired to detonate all balloons.
This question is to find the most overlapping. As like as two peas, the problem is just the same as the interval scheduling algorithm. If there are at most N non overlapping intervals, at least n arrows are required to penetrate all intervals

Replace > = with >
var findMinArrowShots = function(points) {
points.sort((a, b) => {return a[1] - b[1]})
let count = 1, i = 1, end = points[0][1]
for(; i < points.length; i++) {
if(points[i][0] > end) {
// Found the next range to choose
count++
end = points[i][1]
}
}
return count
};
1024. Video splicing (medium) fail
Use the array clips to describe all video clips, where clips[i] = [starti, endi] means that a video clip starts at starti and ends at endi.
You can even freely re clip these clips:
For example, the fragment [0, 7] can be cut into three parts [0, 1] + [1, 3] + [3, 7].
We need to re edit these clips and splice the edited content into clips covering the whole motion process ([0, time]). Returns the minimum number of fragments required, or - 1 if the task cannot be completed.

Important: because the video cannot be disconnected, only the interval with the longest end point can be selected from the overlap
Why reverse order? Because the first interval must be the longest

I chose the first interval as the beginning
var videoStitching = function(clips, time) {
clips.sort((a, b) => { return a[0]==b[0] ? b[1]-a[1] : a[0]-b[0]})
if(clips[0][0] != 0) return -1
if(clips[0][1] >= time) return 1
let res = 1, i = 1, curEnd = clips[0][1], nextEnd = 0
while(i < clips.length && clips[i][0] <= curEnd) {
while(i < clips.length && clips[i][0] <= curEnd) {
nextEnd = Math.max(nextEnd, clips[i][1])
i++
}
// The next interval does not overlap
res++
// Use overlapping and farthest intervals
curEnd = nextEnd
if(curEnd >= time) return res
}
// The farthest overlapping interval cannot be reached
return -1
};
You can also initialize curEnd = 0, that is, the first interval must be < = curEnd = 0
In this way, as long as the end point of the next interval is the farthest, there is no need to arrange in reverse order. (function of the second while loop)
var videoStitching = function(clips, time) {
clips.sort((a, b) => { return a[0]-b[0]})
let res = 0, i = 0, curEnd = 0, nextEnd = 0
while(i < clips.length && clips[i][0] <= curEnd) {
while(i < clips.length && clips[i][0] <= curEnd) {
nextEnd = Math.max(nextEnd, clips[i][1])
i++
}
// The next interval does not overlap
res++
// Use overlapping and farthest intervals
curEnd = nextEnd
if(curEnd >= time) return res
}
// The farthest overlapping interval cannot be reached
return -1
};
This continuous two while loops is also a test of code skills. The first while loop limits the index of the array and fails directly if the partition is disconnected.
The second while loop is to find the farthest overlapping interval.