
35. Search insertion position (simple)
Given a sort array and a target value, find the target value in the array and return its index. If the target value does not exist in the array, return the position where it will be inserted in order.
You must use an algorithm with a time complexity of O(log n).
This is an ordinary binary search. When the target value does not exist, it returns left, because the end condition is left = right + 1. The previous step of the end is divided into: left + 1 = right or left = right; Then, in each case of if else, the subscript of left is the following feature.

392. Judgment subsequence (simple)

Double pointer:
var isSubsequence = function(s, t) {
let i = j = 0, len = s.length;
for (; i<t.length && j<len; i++) {
if(s[j]==t[i]) j++;
}
return j==len
};
Advanced binary search:
If you are given a series of strings s1,s2,... And string t. The time complexity of each s processed by the above solution is still O(N). If binary search is skillfully used, the time complexity can be reduced, which is about O(MlogN), and M is the length of S.

If a series of strings are fast, the connotation means to prepare a dictionary in advance,
It mainly preprocesses t, and uses a dictionary index to store the index position of each character in order

For example, in this case, if "ab" is matched, it should match "c":

According to the previous solution, we need J linear forward scanning character "c". But now, with the help of the information recorded in the index, you can search the index larger than j in index[c]. In the example above, you can search the index larger than 4 in [0,2,6]:
How to use binary search to calculate the index that is just larger than 4? The answer is that you can do a binary search to find the left boundary.
Note that for (let index in t) index is a string
function left_bound(arr, target) {
let left=0, right=arr.length-1;
while (left<=right) {
let mid = Math.floor((right-left)/2) + left;
const val = arr[mid]
if(val == target) {
right = mid - 1
} else if(val < target) {
left = mid + 1
} else {
right = mid - 1
}
}
return left;
}
var isSubsequence = function(s, t) {
let dic = {}
for (let index in t) {
let c = t[index]
if (!dic[c]) {
dic[c] = []
}
dic[c].push(index - 0) // index is converted from a string to an integer
}
// console.log(dic)
let need = 0
for (let c of s) {
// The character c does not exist
if (!dic[c]) return false;
// Find the position of the character c in the dictionary
let pos = left_bound(dic[c], need)
// Binary search has no subscript greater than j
if (pos == dic[c].length) return false;
// j starts at the next of the t string, and the index above the problem is the string
need = dic[c][pos] + 1
}
return true;
};
354. Russian Doll envelope problem (difficult)

It gives me the feeling that there is more dynamic planning. Let's look at the analysis first. The problem is dynamic rule + dichotomy, which needs to be sorted before processing.

Envelope nesting problem of longest increasing subsequence , this topic is actually a variant of the longest increasing subsequence (LIS), because it is obvious that each legal nesting is large and small, which is equivalent to finding a longest increasing subsequence, and its length is the maximum number of envelopes that can be nested.
The solution of this problem is quite ingenious:
First, the width w is sorted in ascending order (one dimension is processed). If w is the same, it is sorted in descending order according to the height H. Then take all h as an array, and calculate the length of LIS on this array is the answer.
The two-dimensional problem is transformed into one-dimensional problem, and a new sequence is constructed

Split + moving gauge In this way, I (I don't even know dynamic programming) won't learn it first and use dynamic programming with time complexity O(N^2). Comfort yourself.

Then solve 300 first Longest increasing subsequence, give you an integer array nums, and find the length of the longest strictly increasing subsequence.

because
d
p
[
i
]
dp[i]
dp[i] can have different meanings, so follow the article. Follow the steps below:
- dp[i] represents the length of the longest increasing subsequence ending with num [i].
- All dp arrays are initialized to 1. Because the subsequence must contain itself at least, the minimum length is 1.
- State transition:
L
[
j
]
=
1
+
m
a
x
(
L
[
i
]
)
,
i
<
j
And
a
[
i
]
<
a
[
j
]
L[j]=1+{max(L[i]), I < J and a [i] < a [J]}
L[j]=1+max(L[i]), I < J and a [i] < a [J]
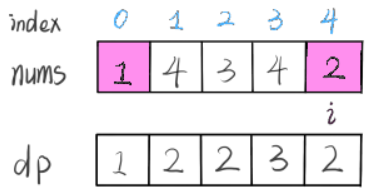
- The final result should be the maximum value in the dp array.

LIS code - leetcode question 300. Dynamic programming,
var lengthOfLIS = function(nums) {
let len = nums.length
let dp = new Array(len).fill(1)
for (let i=1; i<len; i++) {
for (let j=0; j<i; j++) {
if (nums[i] > nums[j])
dp[i] = Math.max(dp[i], dp[j]+1)
}
}
return Math.max(...dp)
};
Envelope nesting problem code - leetcode question 354. Dynamic programming, official problem solving timeout, all languages, shit
Write it down first. I'll be studying then
var maxEnvelopes = function(envelopes) {
// Arrange in ascending order of width, and in reverse order of height if the width is the same
envelopes.sort((a, b) => {
return a[0]==b[0] ? b[1]-a[1] : a[0]-b[0]
})
let len = envelopes.length
const height = new Array(len)
for (let i = 0; i < len; i++) {
height[i] = envelopes[i][1];
}
// LIS problem
let dp = new Array(len).fill(1)
for (let i=1; i<len; i++) {
for (let j=0; j<i; j++) {
if (height[i] > height[j]) // Compare height only
dp[i] = Math.max(dp[i], dp[j]+1)
}
}
return Math.max(...dp)
};
793. K zeros after factorial function (difficult)
Related articles: factorial related algorithm problems

The first reaction seems to be that in the greedy algorithm, we have done a search in turn with the base number of 2, 3 and 5 as the pointer.

The end is 0, which should be related to the two factors of 2 and 5.
It's too simple and too simple
172. Zero after factorial

For example, n = 25, then 25! How many 2 and 5 can be decomposed at most? This mainly depends on how many factors 5 can be decomposed, because each even number can be decomposed into factor 2, which must be much more than factor 5.
The problem turns into: n! How many factors 5 can be decomposed at most?
The difficulty lies in the efficient calculation of factor 5,
125!, 125 divided by 5 = 25 for the first time, indicating that at least one number of 25 can increase by a factor of 5
125 divided by 25 = 5 indicates that there are still five numbers that can increase by two factors 5, but it has been provided once before, and there is one left.
125 divided by 125 indicates that there is still one number that can be increased by three factors 5. It has been increased twice before, and there is one left.
code:
var trailingZeroes = function(n) {
let ans = 0, base = 5;
while (base <= n) {
ans += Math.floor(n / base)
base *= 5
}
return ans;
};
With the increase of N, trailingZeroes(n!) It must be increasing. For this monotonic function, traversing with the for loop can reduce the dimension by binary search.

Binary search requires a search interval

Note: when binary search does not exist, the meaning of left and right

var preimageSizeFZF = function(k) {
let left = 0, right = Number.MAX_SAFE_INTEGER;
// Left Border
while (left <= right) {
let mid = Math.floor((right-left)/2) + left;
const val = trailingZeroes(mid)
if(val == k){
right = mid - 1
} else if(val > k){
right = mid - 1
} else{
left = mid + 1
}
}
let first = left;
left = 0, right = Number.MAX_SAFE_INTEGER;
// right border
while (left <= right) {
let mid = Math.floor((right-left)/2) + left;
const val = trailingZeroes(mid)
if(val == k){
left = mid + 1
} else if(val > k){
right = mid - 1
} else{
left = mid + 1
}
}
// Value range of first=x,right=x-1 when it does not exist
return right - first + 1;
};