Backtracking, greedy, and dynamic planning ideas are developed by doing a lot of exercises, not in a few days, and the title won't tell you which algorithm to use. Keep working on the problem.

Back-tracking - 46. Full arrangement (medium) 51. Queen N (difficult)

Pre-order traversal code executes at the point in time before entering a node, and post-order traversal code executes at the point in time after leaving a node. Path and Selection are attributes of each node

def backtrack(Route, Selection List):
	if Satisfies the end condition:
        result.add(Route)
        return
	for Choice in Selection List:
	    # Make a choice
	    Remove the selection from the selection list
	    Route.add(Choice)
	    backtrack(Route, Selection List)
	    # Undo Selection
	    Route.remove(Choice)
	    Add this selection to the selection list

A slight variation is made here, instead of explicitly recording the Selection List, the current selection list is derived by recording the elements in the trace with a user array.

JS Syntax - Copy Array
[...path]
Array.from(path)
path.slice()

46 Questions
Remember the simplest framework

var permute = function(nums) {
    let used = new Array(nums.length).fill(false)
    let res = [], track = []
    function backtrack(nums, track, used) {
        if(track.length == nums.length) {
            res.push([...track])
            return
        }
        for(let i=0; i<nums.length; i++) {
            if(used[i]) continue
            track.push(nums[i])
            used[i] = true
            backtrack(nums, track, used)
            track.pop()
            used[i] = false
        }
    }
    backtrack(nums, track, used)
    return res;
};

It's all about changing the way you choose and excluding illegal ones.

Each solution contains a different chess placement scheme for the n-queen problem in which'Q'and'.' They represent the Queen and the empty seat.

The difficulty is to return to the required format. The path to the article is a two-dimensional array. I use one-dimensional instead. Test the JS syntax. Understanding of map methods.

51 code questions

var isValid = (row, col, track) => {
    for(let i=0; i<row; i++) {
        if(track[i]==col || Math.abs(track[i] - col) / (row - i) == 1) return false
    }
    return true
}
function transform(track) {
    let n = track.length
    let board = new Array(n).fill(0).map(() => new Array(n).fill('.'))
    for(let i=0; i<n; i++) board[i][track[i]] = 'Q'
    // Does not change the original array
    return board.map((val) => val.join(""))
}
var solveNQueens = function(n) {
    let res = [], track = []
    function backtrack(track, row) {
        // Not n-1
        if(row == n) {
            res.push(transform(track))
            return
        }
        for(let col = 0; col < n; col++) {
            if(!isValid(row, col, track)) continue
            track.push(col)
            backtrack(track, row+1)
            track.pop()
        }
    }
    backtrack(track, 0)
    return res;
};

Article Summary

In fact, backtracking algorithm is actually what we often call DFS algorithm, which is essentially a kind of violence exhaustion algorithm

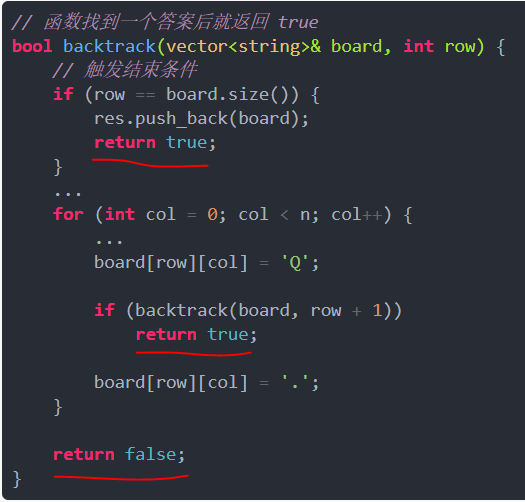
When writing the backtrace function, you need to maintain the Path you have traveled and the Selection List you can currently make. When the End Condition is triggered, you enter the Path in the result set.

Sometimes, we don't want all the legal answers, just one answer. What can we do?
Second return, do not continue looking for Selection List
Third return, there is no appropriate next step in the Choice List to tell the previous layer of failure

Greed - 455. Distribute cookies (simple)

The algorithmic transcript does not summarize the greedy algorithm, because greed has no routine, which is common sense derivation and counter-example verification.

The essence of greed is to select the local optimum for each stage to reach the global optimum.
If the simulation is feasible, you can try out the greedy strategy by manually simulating yourself. If not, you may need to plan dynamically.

Previous Tabi horse races were greedy, 870. Advantage shuffle

455 question codes

var findContentChildren = function(g, s) {
    g.sort((a, b) => b - a) // Appetite
    s.sort((a, b) => b - a) // Biscuits
    let res = 0, index = 0 // Cookie Pointer
    for(let i=0; i<g.length && index<s.length; i++) {
        if(g[i] <= s[index]) {
            res++
            index++
        }
    }
    return res
};

376. Swing Sequence () - Greed or Rule

The difference of the entire sequence of instance 2 is (16, -12, 5, 3, 2, -5, 11, -8)

I don't know what the code says. Look at other people's explanations of leetcode

7. Because we can select at most one of the adjacent identical elements, we can ignore the adjacent identical elements.
8. Elements in the sequence that are neither "peaks" nor "valleys" are referred to as "transitional elements". For example, in the sequence [1,2,3,4][1,2,3,4], 22 and 33 are both "transitional elements".

Greedy Algorithm
Once you understand the concept, it looks like you are looking for mathematical extremes. Then it inexplicably becomes a sliding window of size 3.

Error cases:
[0,0]
1
Error cases:
[4, 2, 2, 4] If the left-right difference is updated every time, the two minimum values are ignored. So it's a double pointer, not a sliding window.
Error cases:
[1,1,1,2,2,2,1,1,1,3,3,3,2,2,2]

If rightDiff is not 0, leftDiff will inherit it negatively because I use the middle number to subtract both sides.
If rightDiff is 0, it is going flat, and leftDiff retains the last slope.

The final boundary case prevents the last rightDiff from being 0, so the extreme value is never found, and the rightmost side is ignored. The way to do this is to see if leftDiff has a slope, then the rightmost side is also the extreme value.
Because the leftmost side must count as one, look at the rightmost side.

var wiggleMaxLength = function(nums) {
    if(nums.length == 1) return 1
    let leftDiff = nums[1] - nums[0], rightDiff = 0, res = 0;
    for(let i = 1; i<nums.length - 1; i++) {
        rightDiff = nums[i] - nums[i+1]
        if(leftDiff * rightDiff > 0) {
            res++
        }
        if(rightDiff) leftDiff = -rightDiff
    }
    board = leftDiff ? 2 : 1
    return res + board
};

dynamic programming algorithm
It won't work either. Or understand the concept of mountains and valleys

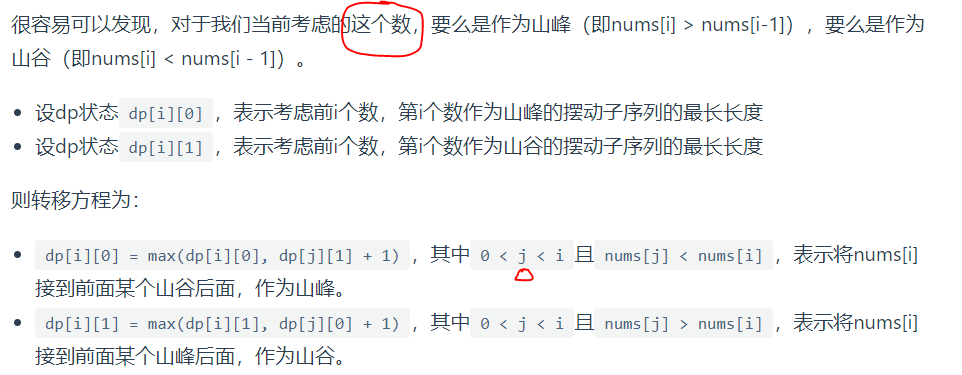
Interpretation is easy at first glance because dynamic programming is difficult: defining array meanings and state transfer equations.
Initialization: Think of the leftmost as an extreme, either a maximum or a minimum, but not necessarily the rightmost.
Equation of State: You can see that if the value of the previous node is the same, the node will not be processed

var wiggleMaxLength = function(nums) {
    let n = nums.length
    if(n == 1) return 1
    const dp1 = new Array(n).fill(1) // Peak
    const dp2 = new Array(n).fill(1) // Mountain valley
    for(let i=1; i<n; i++) {
        for(let j=0; j<i; j++) {
            if(nums[j] > nums[i]) dp2[i] = Math.max(dp2[i], dp1[j]+1)
            if(nums[j] < nums[i]) dp1[i] = Math.max(dp1[i], dp2[j]+1)
        }
    }
    return Math.max(...dp1, ...dp2)
};

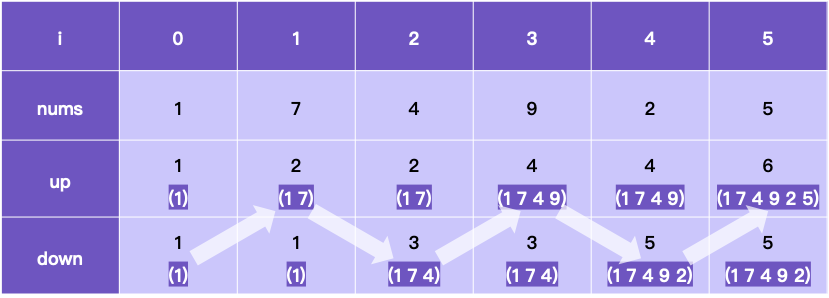
Keeping the maximum values of peaks and valleys makes it unnecessary for j to traverse from 0 to i-1 in the dp transfer equation

This simplification was also tried out. Or it could mean that the nearest mountain to the current Valley must have more nodes.

var wiggleMaxLength = function(nums) {
    let n = nums.length
    if(n == 1) return 1
    let dp1 = 1 // Peak
    let dp2 = 1 // Mountain valley
    for(let i=1; i<n; i++) {
        if(nums[i-1] > nums[i]) dp2 = dp1+1
        if(nums[i-1] < nums[i]) dp1 = dp2+1
    }
    return Math.max(dp1, dp2)
};