Occurrence scenario: it is known that the planned route of the vehicle is from point A to point B, and it is assumed that the vehicle is point G

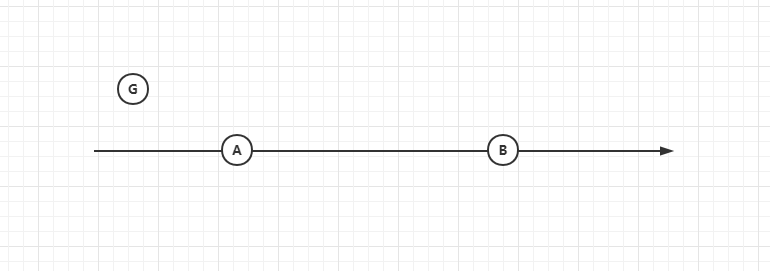
Ask questions:

1. Judge the orientation of point G at point A (front rear relationship)
2. Calculate the distance from point G to point A

Problem analysis:

1. A. B longitude and latitude are specific points on the earth, which do not belong to the same plane. The distance between two points cannot be calculated by linear distance
2. A. The longitude and latitude of two points B are known, and the length of AB is known
3. The longitude and latitude of point G are known, but there will be errors due to GPS positioning and other problems, and point G may appear anywhere
4. The direction is known, from A to B
5. According to the analysis of special cases, point G is just on line AB

Solution:

1. Cosine function (cos) in trigonometric function
2. Special case analysis
3. Due to the error of G-point coordinate, when calculating the distance of GA, there will be greater error by directly calculating the distance between two points

Scheme idea:

1. Judge the orientation of point G at point A (front back relationship)

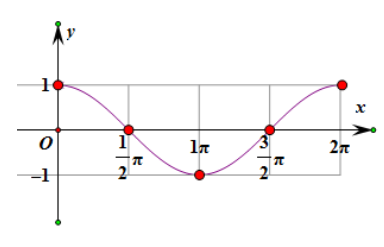
The cos function graph is as follows:

1. According to the analysis of special cases, the coordinates of point G coincide with point A or point B
2. Make AB vertical line L at point A
3. Connect GA and GB two points to form GAB triangle
   
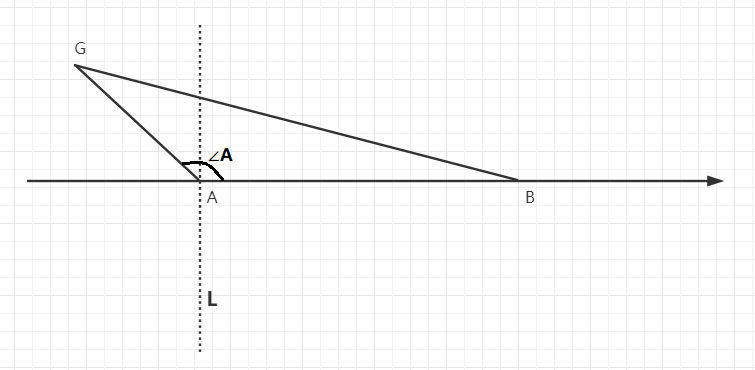
4. The following conclusions may be obtained from the cosine function graph combined with ∠ A:
   
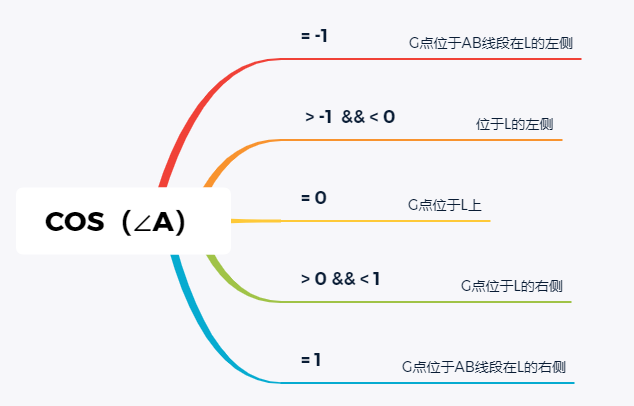
5. Therefore, we can roughly get the general orientation of point G on line AB and point A

2. Judge the distance from point G to point A

It is difficult to completely ignore the calculation result error caused by positioning error. Here I change a way of thinking to deal with this problem. This way of thinking is practical in some specific scenarios, including some related projects I have done.
Ideally, point G should move on line AB, and the distance from point G to point a is directly equal to the actual record between two points. However, due to the error of point G, the probability of point G is not on line AB, so I do not intend to directly calculate the distance of GA, but change point G into a point on line AB, and then calculate the distance from point G to point A. because the AB end is fixed, There is an error in G-point positioning, so the problem caused by this error can be reduced as much as possible.

1. For the three cases where COS(∠ A) is equal to 0, - 1,1, special treatment is made to directly calculate the GA distance.
2. As COS(∠ A) is not equal to the above three situations, make the vertical line from point G to point AB, intersect with line AB at point P, calculate the distance of PA, and calculate the distance of PA as the distance of GA
   
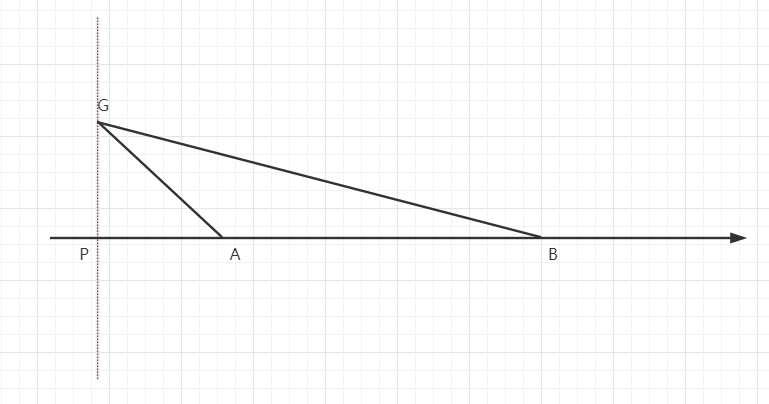
   3. Determine the longitude and latitude coordinates of points g, a and B, first calculate the length of the three sides, and then calculate the PA distance through mathematical method.

JAVA related method implementation:

//π value
private static final double PI = 3.141592653589793238462643383279502884197d;
//Earth radius (m)
private static final double EARTH_RADIUS = 6378137;
/**
 * Angle to radian
 * @param angle angle
 * @return radian
 */
 private static double radianSwitch(double angle){
	return (angle / 360) * 2 * PI;
 }

/**
 * Calculate the distance between two points on the earth
 * @param lng1 angle
 * @return radian
 */
public static double distanceHaversine(double originLng, double originLat, double destinationLng, double destinationLat) {
	double originRadLat = radianSwitch(originLat);
	double destinationRadLat = radianSwitch(destinationLat);
	double a = originRadLat - destinationRadLat;
	double b = radianSwitch(originLng - destinationLng);
	double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(originRadLat) * Math.cos(destinationRadLat) * Math.pow(Math.sin(b / 2), 2)));
	s = s * EARTH_RADIUS;
	s = Math.round(s * 10000) / 10000.0;
	return s;
}

/**
 * Calculate the cos value of ∠ A in triangle ABC
 * @param aLength  ∠A Length of opposite side
 * @param bLength  ∠B Length of opposite side
 * @param cLength  ∠C Length of opposite side
 * @return cos(∠A)
*/
private static double calculateCos(double aLength,double bLength,double cLength){
	return (Math.pow(bLength,2) + Math.pow(cLength,2) - Math.pow(aLength,2))/(2 * bLength * cLength);
}

Delve into the subject

1. The plane trigonometric function is always inconsistent with the actual situation of the earth, so the trigonometric function formula in spherical coordinate system can be considered
2. There are still some errors in the above distance calculation methods, so a more accurate geospatial distance calculation method can be pursued
3. The problem of data cleaning is that not every GPS point is valid data. Some verification should be done to clean out the more outrageous data
4. In practice, it is estimated that the line has an irregular line composed of N points. Considering the special geographical forms such as turning and ring, the selection of reference point B shall be preferred, such as shortening the distance between points AB

reference material

Optimization of geospatial distance calculation - meituan technical team