Skip list
Coupon m.fenfaw netOrdered set is an important data structure in redis. From the name, we can know that it has one more order than the general set. The ordered set of redis will require us to give a score and element, and the ordered set will sort the elements according to the score we give. Redis has two kinds of codes to realize the ordered collection, one is the zip list, the other is the skip list, which is also the protagonist of this chapter. Next, let me lead you to understand the use of ordered sets.
Suppose a software company makes statistics on the programming language mastered by programmers in the company. There are 90 people mastering Java, 20 people mastering C, 57 people mastering Python, 82 people mastering Go, 61 people mastering PHP, 28 people mastering Scala and 33 people mastering C + +. We use an ordered set with key as worker language to store this result.
127.0.0.1:6379> ZADD worker-language 90 Java (integer) 1 127.0.0.1:6379> ZADD worker-language 20 C (integer) 1 127.0.0.1:6379> ZADD worker-language 57 Python (integer) 1 127.0.0.1:6379> ZADD worker-language 82 Go (integer) 1 127.0.0.1:6379> ZADD worker-language 61 PHP (integer) 1 127.0.0.1:6379> ZADD worker-language 28 Scala (integer) 1 127.0.0.1:6379> ZADD worker-language 33 C++ (integer) 1
After forming the above statistical results into an ordered set, we can perform some business operations on the ordered set, such as using ZCARD key to return the length of the set:
127.0.0.1:6379> ZCARD worker-language (integer) 7
The set can be regarded as an array. Use the ZRANGE key start stop [WITHSCORES] command to specify the index interval and return the members in the interval. For example, if we specify start as 0 and stop as - 1, all elements from index 0 to the end of the set will be returned, i.e. [0,6]. If there are 10 elements in the ordered set, then [0, - 1] also represents [0,9], with the WITHSCORES option, In addition to returning the element itself, the score of the element will also be returned. Comparing the order in which we inserted the elements into the ordered set and the order in which we returned the elements below, we can find that the ordered set will sort the elements we inserted.
127.0.0.1:6379> ZRANGE worker-language 0 -1 WITHSCORES 1) "C" 2) "20" 3) "Scala" 4) "28" 5) "C++" 6) "33" 7) "Python" 8) "57" 9) "PHP" 10) "61" 11) "Go" 12) "82" 13) "Java" 14) "90"
Get data for index [2,5]:
127.0.0.1:6379> ZRANGE worker-language 2 5 WITHSCORES 1) "C++" 2) "33" 3) "Python" 4) "57" 5) "PHP" 6) "61" 7) "Go" 8) "82"
In addition to finding elements according to the index, you can also find elements in the score range through ZRANGEBYSCORE key min max [WITHSCORES] [LIMIT offset count] and determine the offset and number of returned elements. Min is the starting score and Max is the ending score. The LIMIT option requires two parameters, offset and count, They are the offset and the maximum entry returned according to the offset.
127.0.0.1:6379> ZRANGEBYSCORE worker-language 25 85 WITHSCORES 1) "Scala" 2) "28" 3) "C++" 4) "33" 5) "Python" 6) "57" 7) "PHP" 8) "61" 9) "Go" 10) "82" #The elements in the [25,85] interval include [Scala,C++,Python,PHP,Go]. With the LIMIT option, only three elements starting from offset 1 (including offset 1) can be queried 127.0.0.1:6379> ZRANGEBYSCORE worker-language 25 85 WITHSCORES LIMIT 1 3 1) "C++" 2) "33" 3) "Python" 4) "57" 5) "PHP" 6) "61"
So far, we have a general understanding of the use of ordered sets. We won't introduce the API of ordered sets too much here. If you are interested, you can refer to the official documents.
Let's talk about the use scenario of ordered collection. Thanks to the ordered collection of Redis, many businesses in high concurrency scenarios can be realized, such as leaderboards and chat services. For example, the hot search of sina Weibo is essentially a ranking list, which sorts topics according to the number of clicks or discussion degree of users on topics; Chat service can also be regarded as a ranking list to some extent, because the earlier chat content is at the top. If we use an ordered set to realize hot search, we can use the topic as the element and the amount of discussion clicked by the user as the score; Similarly, if we use an ordered set to implement the chat service, we can take the user id and user chat content as elements, and the chat timestamp as the score.
From the above business scenarios, you can know that the ordered collection of Redis can adapt to many business scenarios. Next, the author will take you to understand the data structure of the jump table below.
In Redis, if the code of an ordered set is skiplist, the data structure zset is actually used. According to the following excerpts, zset itself contains two data structures: dict and zskiplist. These two data structures are clear at a glance. Dict is a dictionary and zskipplist is a jump table. Why does zset need dict in addition to zskipplist? The author will explain this later. Let's first understand the data structures of zskiplist and zskiplistNode #.
server.h
typedef char *sds;
/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
sds ele;
double score;
struct zskiplistNode *backward;
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span;
} level[];
} zskiplistNode;
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
Looking at zskiplist and zskiplistNode, we can find a header pointer and a tail pointer in the field of zskiplist, and a backward pointer in the field of zskiplistNode. Each element in the level array has a forward pointer. We can guess that the jump table has the characteristics of double ended linked list. In addition to the backward pointer and level array, zskiplistNode also has two fields: ele and score. Ele is a pointer of char type and score is a double type. Therefore, we can basically determine that the elements and scores previously added to the jump table are stored in the data structure zskiplistNode. Each zskiplistNode will have a successor pointer to the element behind it, and each layer in the level array may store a precursor pointer forward and a span span. The forward pointer will point to one, two... N nodes in the front. When we want to find a node, we can traverse from the high level across multiple nodes, This is the name of the jump table.
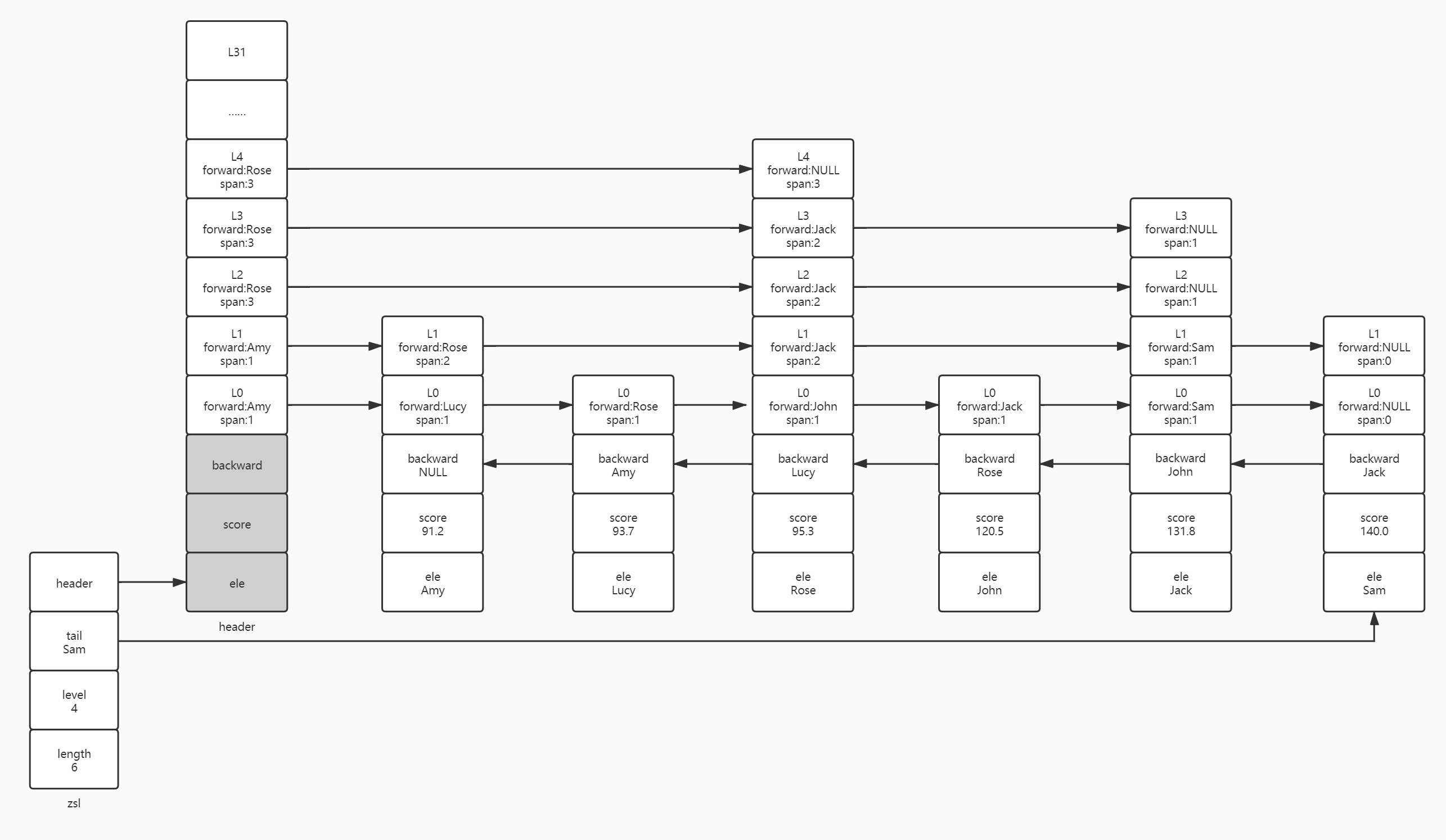
Zskipplist has two fields: length and level. Length represents the number of jump table nodes in the jump table, and level represents the highest layer height of the jump table. Some people may have doubts about the above description of the jump table. Here, the author draws a case diagram of the jump table. We can strengthen our understanding of the jump table according to the following figure.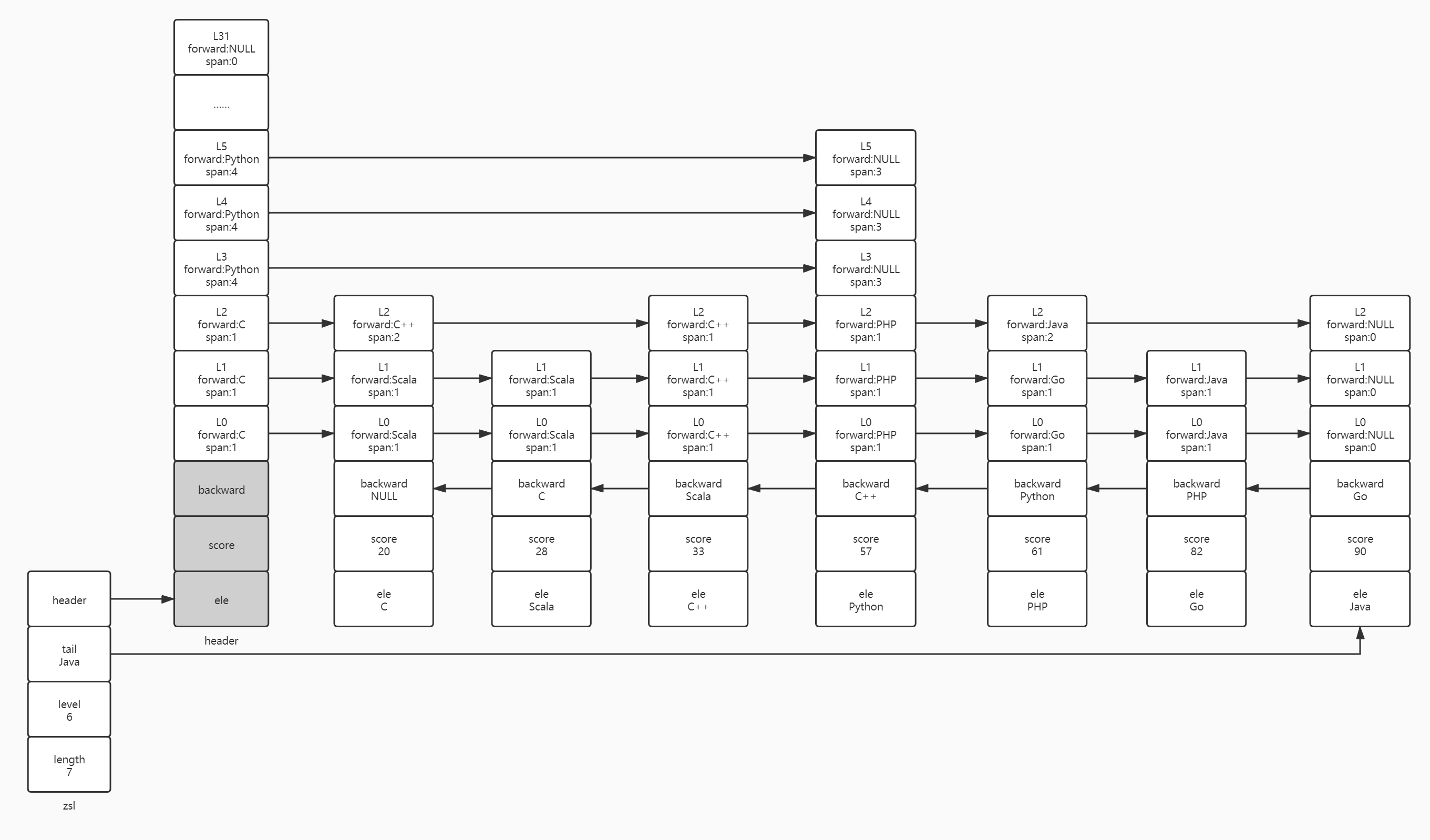
As shown in the above figure, the jump table (zsl) will point to a header. The layer height of this header is generally 32. The header will not store elements (ele) and scores, and there is no subsequent pointer (backward), so the three memory blocks of the header are grayed out. There are 32 layers of zskiplistLevel available in the header. Not all of these 32 layers will be used. It depends on the highest level of the node storing elements and scores. For example, the highest layer in the figure above is the sixth layer of Python node, so the used layer height of the header is also 6. The nodes storing elements and scores will have a random algorithm to generate the layer height. The higher the layer height, the more difficult it is to reach. From the above figure, we can also see that the height of zskiplistLevel of each node is not fixed except the header. The jump layer has two fields: forward and span. Forward is used to store the address of the precursor node. Span (span) has two functions: (1) if forward is not NULL, it is used to record how many nodes the current node needs to go through to reach the precursor node itself. For example, the L3 layer in the header needs to go through four nodes to reach the python node; L2 layer of C node needs to go through 2 nodes to reach C + + node; The L1 layer of Python node needs to go through three nodes to reach the Java node. (2) If forward is NULL, the number of nodes after the current node will be recorded. For example, the python node in the above figure, the forward from L3 to L5 is NULL, and span will record the number of nodes after the python node. If it is a node at the end of the jump table, forward is NULL and span is 0.
Thanks to the non fixed layer height, the jump list has a jump function compared with the general linked list. For example, if we want to check the elements of [80100], we don't need to judge whether the score falls within our range one by one like the linked list. We just need to find the node in the jump list whose score is less than 80 but closest to 80. Here, we can traverse from the highest layer (L5) of the node, Directly reach the python node. The score of the python node is 57, which is less than 80. Therefore, we judge whether the layer contains precursor nodes layer by layer based on the python node level[5]. forward,Python.level[4].forward,Python.level[3].forward is NULL until python level[2]. Forward (PHP) is not empty. PHP is judged here The score is still less than 80, so we go to the PHP node and judge it layer by layer based on the node level[2]. forward. The score (Java.score) is 90 > 80. Here we can't go any further. We still drop layer by layer based on PHP nodes level[1]. forward. The score (Go.score) is 82 > 80. It still can't move forward. It should sink based on the PHP node until PHP level[0]. forward. If the score (Go.score) is 82 > 80, we can determine that the PHP based node is the node that is the smallest but closest to 80. Therefore, based on PHP nodes, we start from L0 one by one to find nodes with scores between [80100]. Here, we start from L0 layer one by one because L0 layer is equivalent to an ordinary linked list and there will be no jumping.
In addition to using scores to find elements, we can also take the jump table as an array and find elements according to the index. For example, if we want to query all elements after index 5, i.e. [5, - 1], we can obtain the length of the jump table and calculate that the end index is 7 + (- 1) = 6, so we just need to find the elements whose index falls in the interval of [5,6] and convert it into span, We are looking for elements whose span falls between [6,7]. Here, we still traverse from the top layer of the node. Starting from the L5 layer of the node, we advance four nodes to the python node itself. At this time, the span is 4, python Level [3,5] has no precursor node, so the Python based node drops to L2, python Level [2] advance a span to the PHP node. At this time, the span is 5. The span of L2 layer in the PHP node is 2,5 + 2 > 6. Therefore, we need to sink a jump layer to L1 and PHP based on the PHP node level[1]. Span is 1, indicating that as long as we advance to PHP level[1]. The node that forward points to is our start node. As long as we find the start node, we can go one by one from the L0 layer of the start node, and finally find the elements whose span falls in [6,7], that is, the index is in [5,6].
So far, we have learned about the structure of the jump table and how it looks up elements according to the score and index. Then next, we need to really enter the source code of the jump table to understand its data structure.
As shown in the following code, when creating the jump table, a memory area will be allocated for the jump table, and the initial layer height is set to 1 and the number of elements is 0. Then, the head node will be created. The layer height of the head node is 32, and the head node has no elements, scores and subsequent pointers. After creating the head node, the precursor pointer of each jump layer of the initialization head node is NULL and the span is 0, Then set the initial tail node of the jump table to NULL, so that a jump table is initialized.
//server.h
#define ZSKIPLIST_MAXLEVEL 32 /* Should be enough for 2^64 elements */
/* t_zset.c
* Create a new skiplist.
Create and return a jump table
*/
zskiplist *zslCreate(void) {
int j;
zskiplist *zsl;
//Allocate space
zsl = zmalloc(sizeof(*zsl));
//Set start level
zsl->level = 1;
//The initial number of elements is 0
zsl->length = 0;
//Initialize header
zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
//Initialize floor height
for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
zsl->header->level[j].forward = NULL;
zsl->header->level[j].span = 0;
}
//Set the following pointer of the header to NULL
zsl->header->backward = NULL;
//The initial footer pointer is NULL
zsl->tail = NULL;
return zsl;
}
//Create jump table element
zskiplistNode *zslCreateNode(int level, double score, sds ele) {
/**
* zskiplistNode The last field is an elastic array, which does not occupy space when calculating the memory occupation. It needs
* Extra level*sizeof(struct zskiplistLevel) bytes are allocated to store the floor height
*/
zskiplistNode *zn =
zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
zn->score = score;
zn->ele = ele;
return zn;
}
Let's simulate how to insert a node into a jump table and look at the jump table below. Assuming that the jump table below saves the weight of employees in a company, regardless of how Amy, Lucy, John, Jack and Sam are inserted into the jump table, we will insert an element with Rose and a score of 95.3 into the jump table based on the existing jump table structure.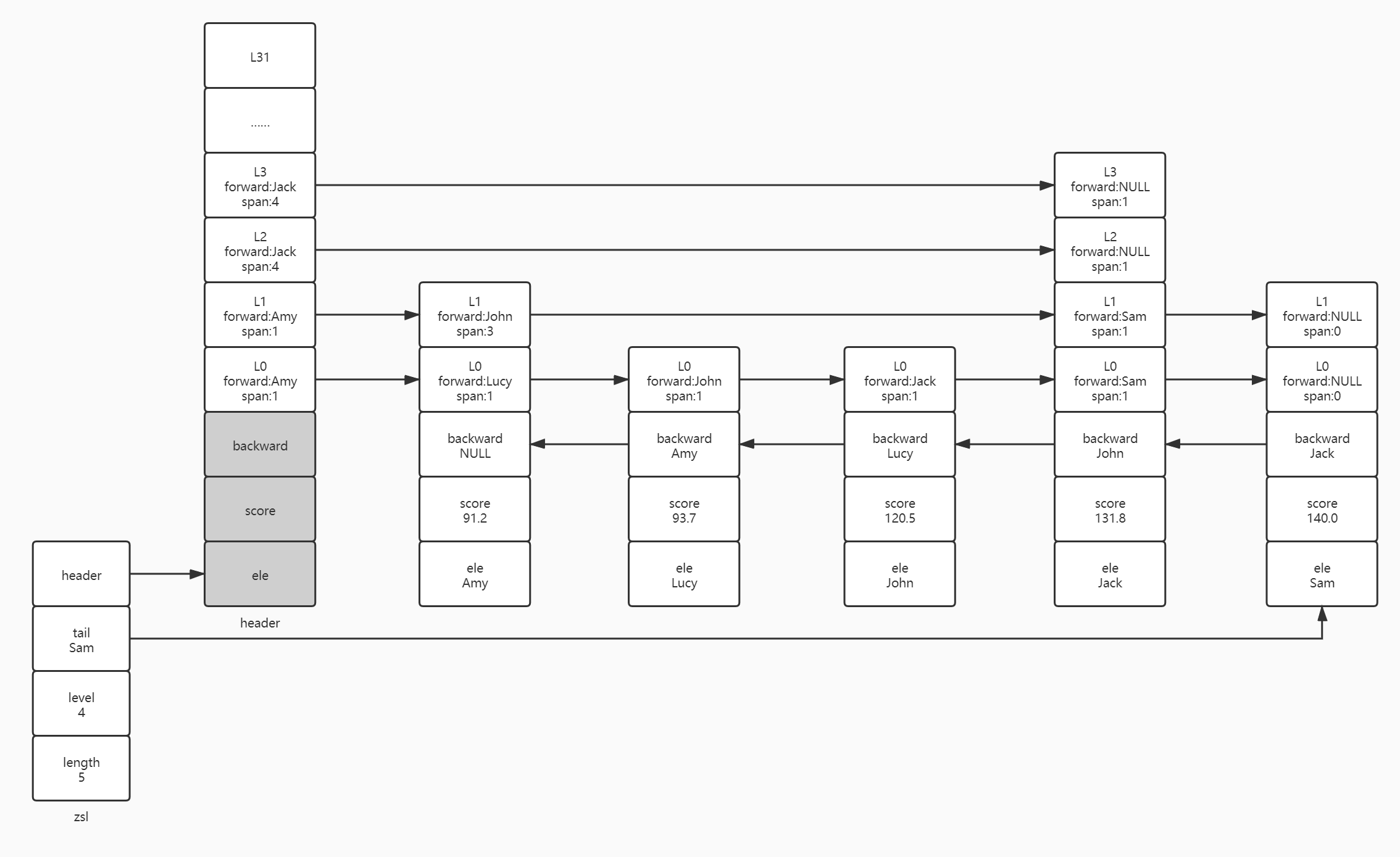
Looking at the whole jump table, we can clearly determine that Rose should be inserted between Lucy and John (93.7 < 95.3 < 120.5), but the computer does not have our God vision, so we still need to find the most suitable position to insert John from the perspective of the computer. Since John wants to become a node in the jump table, it is essential that John must be the precursor node of some nodes and the successor node of some nodes.
First, we need to find out which nodes are likely to become Rose's successor nodes, and record the index of the successor nodes in the jump table (Note: the index here also includes the header node), so as to update the span at the same time when inserting a new node. The index of subsequent nodes starts from the highest level and the initial index value is 0. If the level allows us to enter the next node from the current node, the span of the current node will be added to the index value. The index value of the successor node of the next layer is based on the index value of the previous layer, and then judge whether the node of the current layer is allowed to advance to the next node. If allowed, add the span of the current layer to the index value.
We start from the top layer of the head node. The initial index of the head node is 0 and the head level[3]. forward. The score (Jack.score) is 131.8 due to Jack score>Rose. Score (131.8 > 95.3), so we cannot advance based on the jack node, and the record header is the successor candidate node of layer L3, and the record index of the successor node of layer L3 is 0; Similarly, the header is also the successor candidate node of L2 layer, and the index of the successor node of L2 layer is also 0. When we reach the L1 layer, we judge the header level[1]. forward. Score (Amy.score,96.2) < 120.3, so we advance from the head node to Amy node. When we try to advance to Amy level[1]. When the forward node, judge Amy level[1]. forward. Score (Jack.score) > 120.3 cannot advance, so we record that Amy node is the successor candidate node of L1 layer, and the successor node index of L1 layer is 1. After that, we need to calculate the subsequent nodes and indexes of L0. Here, we no longer advance one by one from the L0 layer of the header node, but advance one by one based on the sinking of Amy node to L0 Before the level [0] layer advances, we first take the index value of the successor node counted by L1 layer as the initial index value of L0 layer, because we start to advance based on Amy node in L0 layer, not based on header node. We need to make up for the index value lost by advancing from header to Amy node in L0 layer. We are based on Amy Level [0] goes all the way to the Lucy node, taking the Lucy node as the successor candidate node of L0 layer, and Lucy can't go to John, so the initial index value of L0 layer + Lucy level[0]. span=1+1=2. So far, we have completed the statistics of successor nodes and their indexes from L3 to L0 in the highest layer. We use two arrays update and rank to record Rose's successor candidate nodes update[Lucy,Amy,header,header] and the index rank[2,1,0,0] of successor nodes in different layers.
It is well understood to record the successor candidate node update of rose. We can assign the predecessor node pointed to by the original successor node to Rose's predecessor node in different layers, and then point the predecessor node of the successor node to rose, which is equivalent to inserting the rose node into the jump table. So how can we update the span according to the subsequent node index of different layers? The result obtained by using rank[0]-rank[i] (I < ZSL - > level) is the number of newly inserted nodes in the middle of the successor nodes of each layer. For example, rank[0]-rank[1]=1, rose node and Amy node are separated by a Lucy node, rank[0]-rank[2]=2, rose node and header node are separated by Amy and Lucy nodes. Therefore, the span from the newly inserted node to the predecessor node is the span of the original successor node - (rank[0]-rank[i]), and the span from the successor node to the newly inserted node is rank[0]-rank[i]+1.
Now, let's generate a random floor height for Rose and create a new node based on the floor height, score and element. Here, we discuss the insertion of John nodes in three cases:
- Rose's floor height is less than the highest level of the current jump table.
- Rose's floor height is equal to the highest level of the current jump table.
- Rose's floor height is higher than the current jump table.
First, let's discuss the case that rose's floor height is less than the highest level. Assuming that the random algorithm generates the floor height of L1 for rose, we update the reference of the jump table from L0. From the above analysis results, we can know that rose's L0 successor node is Lucy, and we assign Lucy's predecessor node to Rose's predecessor node: rose level[0]. forward=Lucy. level[0]. Forward (John), and then we update the precursor node of Lucy to Rose: Lucy level[0]. Forward = rose, then we need to update the span of Lucy and rose nodes on L0 layer. Since it is on L0 layer, which is equivalent to an ordinary linked list, the span between Lucy and rose on L0 layer and that between rose and John on L0 layer are both 1.
Then, we are updating the reference and span of L1 layer. The successor node of rose in L1 layer is Amy. Here, we still assign the precursor pointed by Amy in L1 to Rose's precursor in L1: rose level[1]. forward=Amy. level[1]. Forward (Jack), and then point Amy's precursor in L1 to Rose: Amy level[1]. forward=Rose. Next, we update the span of Amy and rose. Here, we update the span of rose pointing to Jack first, and then update Rose: the span of Amy pointing to rose, because the span of Amy pointing to jack on L1 floor: rose is needed to update the span of rose pointing to Jack level[1]. span=Amy. level[1]. Span - (rank [0] - rank [1]) = 2, then update the span Amy points to Rose: Amy level[1]. span=(rank[0]-rank[1])+1=2.
The successor nodes of L2 and L3 layers are both header s. Since the Rose node does not have enough floor height to point to, here we simply add + 1 to the span of the successor nodes of L2 and L3.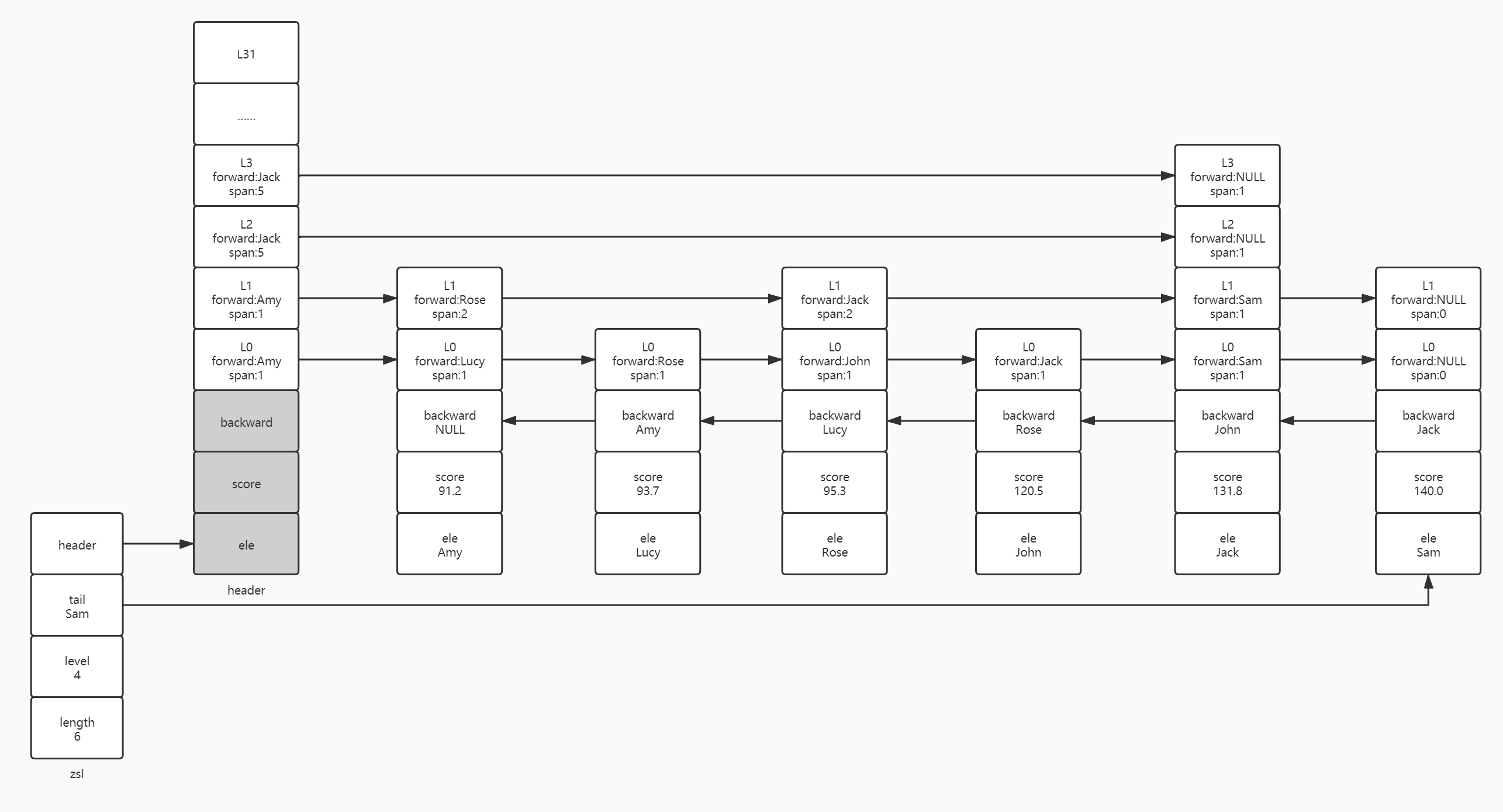
Next, let's consider the second case. If the layer height generated for rose is just equal to the current layer height of the jump table, that is, the layer height of Roese is L3. Here, we continue the previous idea, first update the span of the predecessor node of the newly inserted node, and then update the span of the successor node pointing to the new node. How to update rose nodes L0 and L1 depends on the previous step, which will not be repeated here. We start the update from L2. Here, the author re pastes the following candidate nodes before the above rose node is inserted. Update: [Lucy,Amy,header,header] and the index rank: [2,1,0,0] of subsequent nodes in different layers. First, assign the precursor pointed by the successor node of L2 to the precursor of rose node L2: rose level[2]. forward=header. level[2]. Forward (Jack), and then point the precursor of the L2 successor node to the rose node: header level[2]. forward=Rose. Then we update the span, rose level[2]. span=header. level[2]. span-(rank[0]-rank[2])=4-2=2,header.level[2].span=(rank[0]-rank[2])+1=3. L3 is the same logic as L2, so it will not be demonstrated here.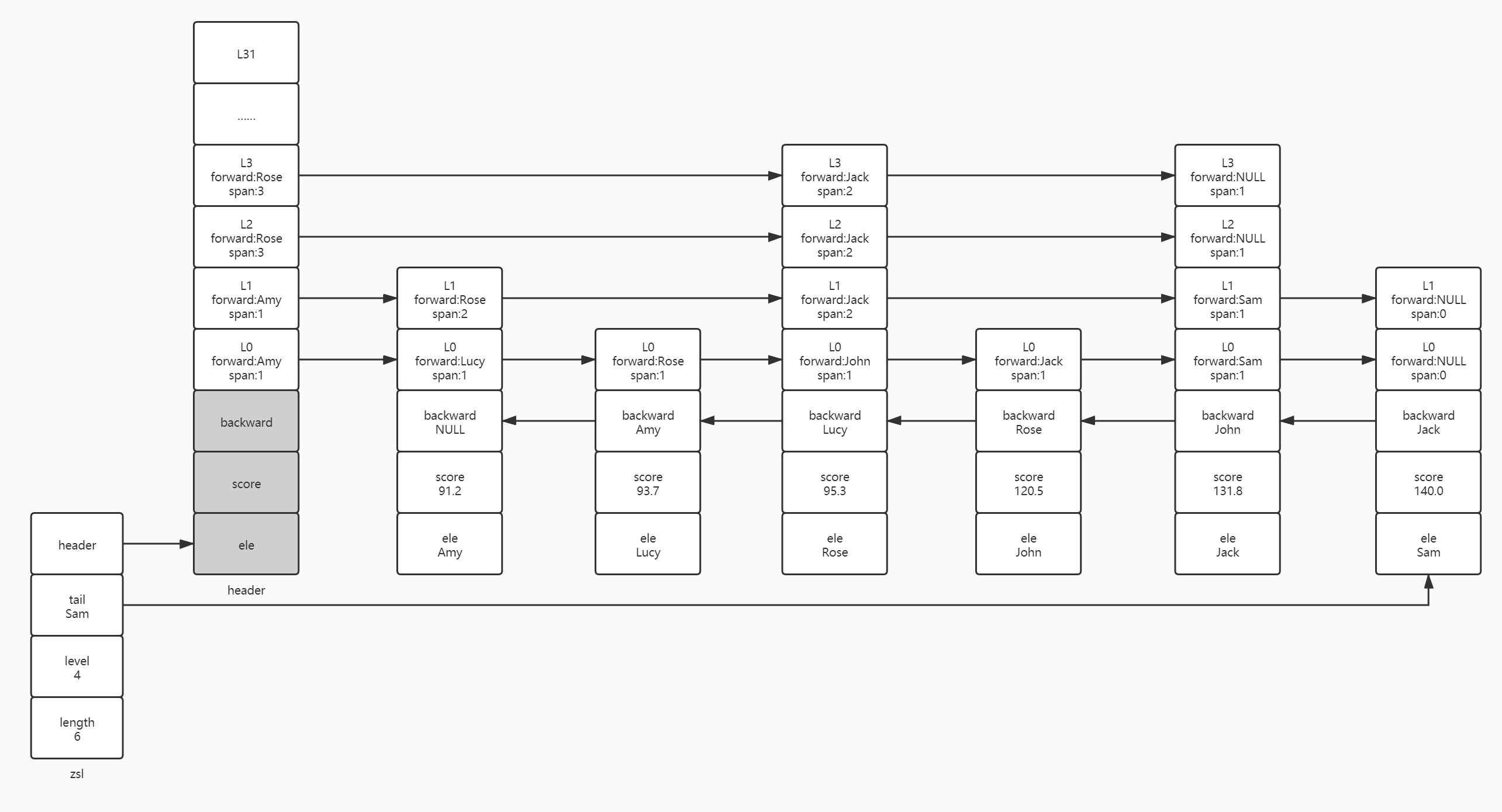
Finally, we consider that the rose node is larger than the top layer of the jump table. First of all, let's think about it. Suppose that the floor height generated by the random algorithm for rose is L4, L5... L6 or even L31. At present, the highest level of the jump table is L3. What are the subsequent nodes higher than the floor height after L3? There is only the head node, so the index of the successor node higher than the jump table is ready, and the index of the head node can only be 0. Therefore, our update and rank arrays need to be updated to [Lucy, Amy, header, header... Header] and [2,1,0,0... 0], so how to calculate the span of the new floor height? Firstly, the span from the head node to the new node is still (rank[0]-rank[n])+1. Secondly, the precursor node of the floor height of the new node > L3 is NULL. The span of the floor height should be updated to the number of nodes after the current node. You need to subtract the number of nodes from the newly inserted node to the successor node (head node) from the number of elements in the jump table, that is, ZSL length - (rank [0] - rank [n]) = 5-2 = 3 (n > 3). Therefore, as long as the floor height of rose node is greater than L3, the forward above L3 is NULL, the span is the number of nodes after Rose (John, Jack, Sam), and the header The span from level [n] to rose is (rank[0]-rank[n])+1=2+1=3 (n > 3).
According to the idea of inserting new nodes into the jump table simulated by the author, let's see how Redis is implemented:
/* Insert a new node in the skiplist. Assumes the element does not already
* exist (up to the caller to enforce that). The skiplist takes ownership
* of the passed SDS string 'ele'.
* Insert a new node into the jump table.
* */
zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) {
/*
* update Array will record the successor node of each layer closest to the newly inserted node, rank array
* The index of the successor node closest to the newly inserted node.
*/
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
unsigned int rank[ZSKIPLIST_MAXLEVEL];
int i, level;
serverAssert(!isnan(score));
x = zsl->header;//<1>
//Starting from the top layer of the head node, find the successor node of each layer closest to the new node
for (i = zsl->level - 1; i >= 0; i--) {
/* store rank that is crossed to reach the insert position
* rank The array records the index of the successor node of each layer closest to the new node. When searching from the top layer, the initial index is 0,
* That is, the initial rank [ZSL - > level-1] = 0. If you can advance from the current node to the next node, the span of the current node will be changed
* Add to index value. When the subsequent node closest to the new node can not move forward, it will sink one layer,
* Based on the current subsequent nodes, continue to try to advance to layer i-1, and the initial index value of layer i-1 is the last statistical value of layer i
* Index value, because the i-1 layer will not advance from the header node one by one, but based on the node to which the previous layer advances, so
* To make up for the index of i-1 layer, make up for the index value of the header advancing to the current node.
*/
rank[i] = i == (zsl->level - 1) ? 0 : rank[i + 1];
/*
* x The initial value is header (see < 1 >),
* That is, the precursor node pointed by X in layer i may become the successor node of the new node, but whether x can move forward needs to be further judged. Here are
* Two conditions determine progress:
* 1.If the score of the X precursor node is less than the score of the new node, it can advance (x - > level [i]. Forward - > score < score)
* 2.If the score of the predecessor node is the same as that of the new node, and the string of the predecessor node is less than that of the new node, it is allowed to advance. be careful:
* The comparison string here is not the length of the comparison string. Sdscmp (x - > level [i]. Forward - > ele, ELE) will be called further
* The function memcmp(s1,s2,n) compares the first n bytes of s1 and s2 of two strings.
* (x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele,ele) < 0)
*/
while (x->level[i].forward &&
(x->level[i].forward->score < score || //
(x->level[i].forward->score == score &&
sdscmp(x->level[i].forward->ele, ele) < 0))) //
{
/*
* If it is determined that node x can advance to the previous node, the span of the current node is added to the index value,
* And update the memory area pointed to by x to the next node.
*/
rank[i] += x->level[i].span;
x = x->level[i].forward;
}
//x advances until it cannot go any further, that is, the node pointed to by x is the successor node of layer i closest to the new node. Record the successor node
update[i] = x;
}
/* we assume the element is not already inside, since we allow duplicated
* scores, reinserting the same element should never happen since the
* caller of zslInsert() should test in the hash table if the element is
* already inside or not.
*
* */
/*
* Here, a layer height will be generated by random algorithm. The higher the layer height, the more difficult it is to generate,
* And the floor height must be < = zskiplist_ MAXLEVEL, attached below
* Generate layer high code.
*/
level = zslRandomLevel();
/*
* If the currently generated layer height is greater than the highest layer height of the jump table, you need to update ZSL - > level
* The successor node and node index of the layer. Subsequent nodes of ZSL - > level or higher can only be header nodes,
* Therefore, the indexes of subsequent nodes are all 0. At the same time, the span of these subsequent nodes is the number of nodes in the jump table, which is convenient for updating
* Subsequent updates span.
*/
if (level > zsl->level) {//<2>
for (i = zsl->level; i < level; i++) {
rank[i] = 0;
update[i] = zsl->header;
update[i]->level[i].span = zsl->length;
}
//Update the jumping surface height to the currently generated floor height
zsl->level = level;
}
//Create a jump table node based on the floor height, branches, and elements
x = zslCreateNode(level, score, ele);
//Insert the new node into the jump table and update the span
for (i = 0; i < level; i++) {
/*
* update[i]For the successor node of the new node in layer i, update the precursor pointed by the new node in layer i
* The precursor pointed to by the successor node. Then update the predecessor of the successor node in layer i to a new node. So,
* The new node is inserted into the jump table.
*/
x->level[i].forward = update[i]->level[i].forward;
update[i]->level[i].forward = x;
/* update span covered by update[i] as x is inserted here
* (rank[0] - rank[i])How many nodes are separated between the new node and the successor node of layer i,
* In layer I, the span from X to the precursor node (x - > level [i]. Span) is subtracted from the span of the original successor node
* Number of nodes between new nodes and layer i successor nodes:
* (update[i]->level[i].span - (rank[0] - rank[i]))
* The span of the successor node in the new node is: (rank[0] - rank[i]) + 1
* If the program has previously entered the branch < 2 >, that is, the floor height generated by executing level = zslRandomLevel()
* The height is greater than the layer height of the original jump table. For example, if the original ZSL - > level is 3, but the level generation is 10, the new nodes L3~L9
* The successor node of is the head node, the index value of the successor node is 0, the precursor of the new node L3~L9 is NULL, and the span is after the new node
* And ZSL - > length - (rank [0] - rank [i]) is the number of nodes after the new node.
*/
x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
update[i]->level[i].span = (rank[0] - rank[i]) + 1;
}
/* increment span for untouched levels
* If level = zslRandomLevel(), the generated floor height is greater than that of the original ZSL - > level
* If the floor is high, it will not enter this cycle. Only when the generated floor height is less than the original floor height of ZSL - > level,
* You need to add 1 to the span of the subsequent node of level < = I < ZSL - > level, because a new node is inserted.
*/
for (i = level; i < zsl->level; i++) {
update[i]->level[i].span++;
}
/*
* L0 Layer is equivalent to an ordinary linked list. If the successor node of the newly inserted node in layer L0 is a header, the backward of the new node points to NULL,
* Otherwise, it points to the successor node closest to the new node in the jump table.
*/
x->backward = (update[0] == zsl->header) ? NULL : update[0];
/*
* If the new node is not the end node, point the backward pointer of the precursor pointer of the new node to the new node,
* Otherwise, the pointer at the end of the jump table will point to the new node.
*/
if (x->level[0].forward)
x->level[0].forward->backward = x;
else
zsl->tail = x;
//After inserting a new node, add 1 to the number of elements in the jump table
zsl->length++;
return x;
}
Generate floor height zslRandomLevel(void):
/* Returns a random level for the new skiplist node we are going to create.
* The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
* (both inclusive), with a powerlaw-alike distribution where higher
* levels are less likely to be returned.
*
* Skiplist P = 1/4
* while In circulation
* The probability that the cycle is true is P(1/4)
* The probability that the cycle is false is (1 - P)
*
* The probability that the floor height is 1 is (1 -P)
* The probability of floor height of 2 is P *(1 -P)
* The probability of floor height of 3 is P^2 *(1 -P)
* The probability of floor height of 4 is P^3 *(1 -P)
* The probability of floor height n is P^(n-1) *(1 -P)
*
* Therefore, the average floor height is
* E = 1*( 1-P) + 2*P( 1-P) + 3*(P^2) ( 1-P) + ...
* = (1-P) ∑ +∞ iP^(i-1)
* i=1
*
* =1/(1-P)
*
* */
int zslRandomLevel(void) {
int level = 1;
while ((random() & 0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
level += 1;
return (level < ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}