1, Concept
A Graph is a structure used to represent a certain relationship between objects. The "object" after mathematical abstraction is called a Vertex, node or point, and the correlation between nodes is called an edge. When drawing a Graph, nodes are usually represented by a group of points or small circles, and the edges between them use lines or curves.
1. Directed graph and undirected graph
Edges in a graph can be directional or undirected.
For example, in a diagram, if the node represents the people at the party and the edge represents that the two people have shaken hands, the diagram has no direction, because a and B shook hands, which also means that B must have shaken hands with a. On the contrary, if an edge from a to B represents the money a owes B, the graph has a direction, because the relationship of "once owed money" is not necessarily two-way. The former is called undirected graph, and the latter is called directed graph.
At the same time, an undirected graph can also be considered as A directed graph, that is, it can be imagined that there are edges from A to B and edges from B to A between two nodes. Therefore, from A broad perspective, all graphs can be considered as directed graphs.
2, Representation of Graphs
Representations in textbooks: adjacency table and adjacency matrix
1. Adjacency table
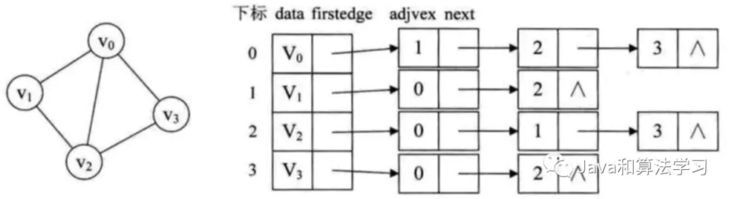
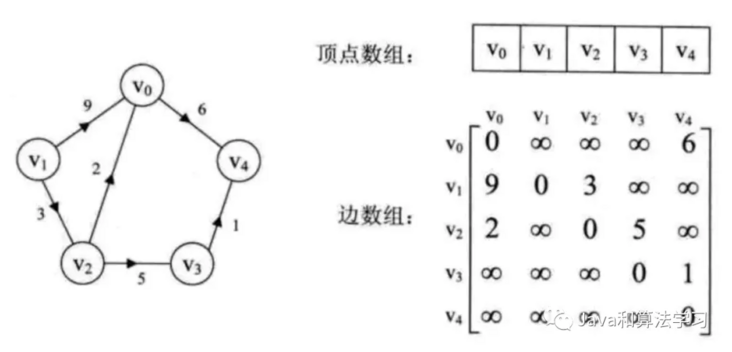
2. Adjacency matrix
If graph G has n nodes, the adjacency matrix is an n*n matrix, which is defined as:
G [i] [J] = 1 (or weight value), if < VI, VJ > is the edge in G; Otherwise, G [i] [J] = infinity. For the setting of diagonal, set it according to the situation.
3. Common notation
The above two representations will hardly be encountered in the actual problem brushing process.
More importantly, give you an n*3 matrix [[weight, fromNode, toNode]], such as [[3, A, B], [2, B, M], [5, A, R]]. The first value represents the weight, the second value represents the from node, and the third value represents the to node. That is, the direct representation of an edge.
3, Solution of graph
The algorithm of graph is not difficult, but the cost of coding is relatively high
(1) First, use your most skilled way to realize the expression of graph structure
(2) On the familiar structure, implement all commonly used graph algorithms as templates
(3) Convert the graph structure provided by the interview question into your familiar graph structure, and then call the template or rewrite it
There are so many ways to represent a graph, and the forms given to you may be different each time, so it is necessary to abstract one's own representation method. In the future, for different forms, write a method that can be converted into its own defined form (with the feeling of an adapter), so as to respond to changes with invariance and convert unfamiliar representation methods into their own familiar methods
/**
* Information of custom graph
*
* @author Java And algorithm learning: Monday
*/
public class Graph {
/**
* Point set, Key: the point given by the user, Value: user-defined point information
*/
public HashMap<Integer, Node> nodes;
/**
* Edge set
*/
public HashSet<Edge> edges;
public Graph() {
this.nodes = new HashMap<>();
this.edges = new HashSet<>();
}
/**
* Convert the matrix of {N*3} representing edges entered by the user into a user-defined graph
*
* @param matrix N*3 Matrix, [3, 0, 5], [2, 2, 5]
*/
public static Graph createGraph(int[][] matrix) {
Graph graph = new Graph();
for (int[] m : matrix) {
//Get the weight information of the edge and the from and to nodes of the edge given by the user
int weight = m[0];
int from = m[1];
int to = m[2];
//Add point set information of graph
if (!graph.nodes.containsKey(from)) {
graph.nodes.put(from, new Node(from));
}
if (!graph.nodes.containsKey(to)) {
graph.nodes.put(to, new Node(to));
}
//Information of the edge generated by the root site
Node fromNode = graph.nodes.get(from);
Node toNode = graph.nodes.get(to);
Edge edge = new Edge(weight, fromNode, toNode);
//Node information processing
//Add a node directly connected from the current node and an edge directly connected from the current node
fromNode.nexts.add(toNode);
fromNode.edges.add(edge);
//In and out modification
fromNode.out++;
toNode.in++;
//Add edge set information of graph
graph.edges.add(edge);
}
return graph;
}
}
4, Width first and depth first traversal of Graphs
1. Width first traversal
(1) Prepare A queue and A Set (storing traversed nodes and registration table), the starting node is A, and put A into the queue and Set
(2) Pop up the vertex m of the queue and print the value of M. Get the next of all neighbor nodes of M and check whether there are these next nodes in the Set. If not, put them in the Set and queue. If there are, skip this next node
(3) Continue with step 2 until the queue is empty
/**
* Graph width first traversal
*
* @author Java And algorithm learning: Monday
*/
public static void bfs(Node node) {
if (node == null) {
return;
}
Node current = node;
Queue<Node> queue = new LinkedList<>();
HashSet<Node> set = new HashSet<>();
queue.add(current);
set.add(current);
while (!queue.isEmpty()) {
current = queue.poll();
System.out.println(current.value);
for (Node next : current.nexts) {
if (!set.contains(next)) {
queue.add(next);
set.add(next);
}
}
}
}
2. Depth first traversal
Go straight before you finish a road. Go back after you finish to see which fork roads have not been taken. (if you can't go out of the ring road, you can't go any further)
(1) Prepare A stack (storing the whole current path) and A Set (storing the traversed nodes and registration form). The starting node is A. put A into the stack and Set, and print the value of A at the same time (print when entering the stack)
(2) Pop up the stack top element M, traverse all the neighbor nodes next of M, and check whether there are these next nodes in the Set. If not, put m and the next node at this time into the stack, put the next into the Set, print the value of the next (print when it is stacked), and terminate the traversal of the next node (that is, only one node not included in the Set is stacked)
(3) Continue with step 2 until the stack is empty
/**
* Depth first traversal of Graphs
*
* @author Java And algorithm learning: Monday
*/
public static void dfs(Node node) {
if (node == null) {
return;
}
Stack<Node> stack = new Stack<>();
HashSet<Node> set = new HashSet<>();
Node current = node;
stack.add(current);
set.add(current);
//Print on stack
System.out.println(current.value);
while (!stack.isEmpty()) {
current = stack.pop();
for (Node next : current.nexts) {
if (!set.contains(next)) {
stack.add(current);
stack.add(next);
set.add(next);
System.out.println(next.value);
//Stack only one node that is not included in the Set
break;
}
}
}
}
3. Topological ordering of Graphs
Only directed acyclic graphs have topological ordering
(1) Print nodes with 0 degree in the current drawing (multiple nodes with 0 degree can be printed first)
(2) Remove the printed nodes from the graph (naturally, the edges directly connected to these nodes are also removed)
(3) Continue to perform steps 1 and 2 until the node of the graph is empty
/**
* Topological ordering of Graphs
*
* @author Java And algorithm learning: Monday
*/
public static List<Node> topologySort(Graph graph) {
// Key: node, Value: residual penetration
HashMap<Node, Integer> inMap = new HashMap<>();
//Save nodes with degree 0
Queue<Node> zeroInQueue = new LinkedList<>();
for (Node node : graph.nodes.values()) {
//Put all nodes in the initially given graph into the inMap
inMap.put(node, node.in);
if (node.in == 0) {
//Nodes with initial penetration of 0
zeroInQueue.add(node);
}
}
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
Node current = zeroInQueue.poll();
result.add(current);
for (Node next : current.nexts) {
//Reduce the penetration of the neighbor node of the traversed node by one (it can be understood as removing the current node from the graph)
inMap.put(next, inMap.get(next) - 1);
if (inMap.get(next) == 0) {
//The modified node penetration is 0 and placed in the zeroInQueue queue queue
zeroInQueue.add(next);
}
}
}
return result;
}
5, Minimum spanning tree algorithm
It is required to be an undirected graph. When all points are connected, the tree is formed by the edge with the smallest added multiple values of ownership.
1. Kruskal algorithm
Use and query set
(1) Always start from the edge with the smallest weight and find the edge with the larger weight in turn (choose any one with equal weight)
(2) If the current edge enters the set of the minimum spanning tree and does not form a ring, the current edge is required; Otherwise abandon
(3) After finding all the edges, the set of minimum spanning trees is obtained
/**
* Kruskal Algorithm - use parallel search set
*
* @author Java And algorithm learning: Monday
*/
public static Set<Edge> kruskal(Graph graph) {
UnionFind unionFind = new UnionFind(graph.nodes.values());
//Small root heap based on weight value
PriorityQueue<Edge> smallEdgeQueue = new PriorityQueue<>((a, b) -> a.weight - b.weight);
//Put the small root pile into all edges
for (Edge edge : graph.edges) {
smallEdgeQueue.offer(edge);
}
Set<Edge> result = new HashSet<>();
while (!smallEdgeQueue.isEmpty()) {
Edge edge = smallEdgeQueue.poll();
//The node corresponding to the edge at the top of the small root heap will not form a ring (that is, the two points are not in the same set) before it is added to the result set, otherwise it is discarded
if (!unionFind.isSameSet(edge.from, edge.to)) {
result.add(edge);
unionFind.union(edge.from, edge.to);
}
}
return result;
}
2. Prim algorithm
(1) The minimum spanning tree can be found from any node
(2) When a point is added to the selected point, all new edges starting from this point are unlocked
(3) Select the smallest edge among all unlocked edges, and then see if this edge will form a ring after it is added to the unlocked point
(4) If yes, discard the current edge and return to step 3; If not, keep the current edge, unlock the pointing point of the edge, add this edge to the result, and return to step 2
(5) When all points are unlocked, the minimum spanning tree is obtained
/**
* Minimum spanning tree algorithm Prim algorithm
*
* @author Java And algorithm learning: Monday
*/
public static Set<Edge> prim(Graph graph) {
Collection<Node> nodes = graph.nodes.values();
if (nodes.isEmpty()) {
return null;
}
//The unlocked edges are placed in the small root heap according to the weight value standard
PriorityQueue<Edge> smallEdgeQueue = new PriorityQueue<>((a, b) -> a.weight - b.weight);
//Unlocked points
Set<Node> nodeSet = new HashSet<>();
Set<Edge> result = new HashSet<>();
// 1. Starting from any node to find the minimum spanning tree
for (Node node : nodes) {
if (!nodeSet.contains(node)) {
//Point unlock
nodeSet.add(node);
// 2. All edges connected at this point are unlocked
for (Edge edge : node.edges) {
smallEdgeQueue.offer(edge);
}
// 3. Select the smallest edge among all unlocked edges, and then see if this edge will form a ring after it is added to the selected point
while (!smallEdgeQueue.isEmpty()) {
//Pops the smallest edge from the unlocked edges
Edge currentEdge = smallEdgeQueue.poll();
Node toNode = currentEdge.to;
//If the pointing point of the edge is not unlocked, it is unlocked
if (!nodeSet.contains(toNode)) {
nodeSet.add(toNode);
result.add(currentEdge);
//Unlock all edges connected to points
for (Edge edge : toNode.edges) {
smallEdgeQueue.offer(edge);
}
}
//The pointing point of this edge has been unlocked. Discard this edge directly
}
//In order to prevent the forest, so do not break
//If you know clearly that there will be no forest (or there is no need to prevent forest), you can break
// break;
}
}
return result;
}
6, Dijkstra algorithm (dijestra algorithm)
1. Meaning
Take a vertex as the source node, and then find the shortest path from the vertex to all other nodes in the graph, regardless of the unreachable nodes. The algorithm solves the single source shortest path problem with weight on the graph.
2. Function
It is often used in routing, pathfinding, transportation and planning. For example, if the vertices in the graph represent cities and the weights on the edges represent the driving distance between cities, the algorithm can be used to find the shortest path between two cities.
It should be noted that the Dijkstra algorithm is used to process graphs with directed and non negative weights.
3. Code ideas
(1) Define A Map to store the distance from the specified point A to the target point. Starting from the specified point A, the distance to the target point A is 0. The distance from the point A can directly reach in one step is equal to the weight value on the edge, and the distance from the point A cannot directly reach is infinite. Update the Map. Point A is locked.
(2) Find the edge B with the smallest weight to the target point from the Map. If the distance from B to point C in one step plus the distance from A to B obtained in step 1 is less than the distance from A to C obtained in step 1 [(A - > b) + (B - > C) < (A - > C)], update the distance from B to C in the Map, otherwise it remains unchanged; According to this condition, always check the distance from all points that B can directly reach in one step. After the inspection, point B will be locked.
(3) Continue with step 2 until all points are locked.
/**
* Dijkstra Algorithm - original version
*
* @author Java And algorithm learning: Monday
*/
public static Map<Node, Integer> dijkstra1(Node head) {
//Distance from head to target point, key: target point, value: distance
Map<Node, Integer> distanceMap = new HashMap<>();
//The shortest distance from oneself to oneself must be 0
distanceMap.put(head, 0);
//Locked points
Set<Node> selectedNode = new HashSet<>();
//At this time, minNode must be the head point
Node minNode = getMinDistanceFromUnSelectedNode(distanceMap, selectedNode);
while (minNode != null) {
//Shortest distance from head to minNode
int distance = distanceMap.get(minNode);
for (Edge edge : minNode.edges) {
Node toNode = edge.to;
if (!distanceMap.containsKey(toNode)) {
//If toNode does not exist, the shortest distance from head to toNode is the shortest distance from head to minNode + the weight value of this side
distanceMap.put(toNode, distance + edge.weight);
} else {
//If toNode exists, the shortest distance is updated
distanceMap.put(toNode, Math.min(distanceMap.get(toNode), distance + edge.weight));
}
}
//minNode mission completion (all direct points of minNode are traversed)
selectedNode.add(minNode);
//Find the next minNode again
minNode = getMinDistanceFromUnSelectedNode(distanceMap, selectedNode);
}
return distanceMap;
}
4. Using enhanced heap optimization
Enhanced heap can be used to improve. Adjust the time complexity of finding the point with the shortest distance from the unlocked target point in the Map from O(N) to O(logN) level.
/**
* Improved dijkstra algorithm
*
* Starting from the head, all nodes that can be reached by the head generate the shortest path record to each node and return it
*
* @author Java And algorithm learning: Monday
*/
public static Map<Node, Integer> dijkstra1(Node head, int size) {
//Optimize with enhanced heap
NodeHeap nodeHeap = new NodeHeap(size);
//The distance from head to head must be 0
nodeHeap.addOrUpdateOrIgnore(head, 0);
Map<Node, Integer> result = new HashMap<>();
while (!nodeHeap.isEmpty()) {
NodeRecord record = nodeHeap.pop();
Node node = record.node;
int distance = record.distance;
for (Edge edge : node.edges) {
nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);
}
result.put(node, distance);
}
return result;
}
7, All code addresses in this article
Github: https://github.com/monday-pro/algorithm-study/tree/master/src/basic/graph
Gitee: https://gitee.com/monday-pro/algorithm-study/tree/master/src/basic/graph