1, Hill sort
thinking
Firstly, the table to be sorted is divided into several "special" sub tables in the form of L[i,i+d,i+2d,..., i+kd], and each sub table is directly inserted and sorted. Reduce the increment D and repeat the above process until d=1
That is, first pursue the partial order of the elements in the table, and then gradually approach the global order
process

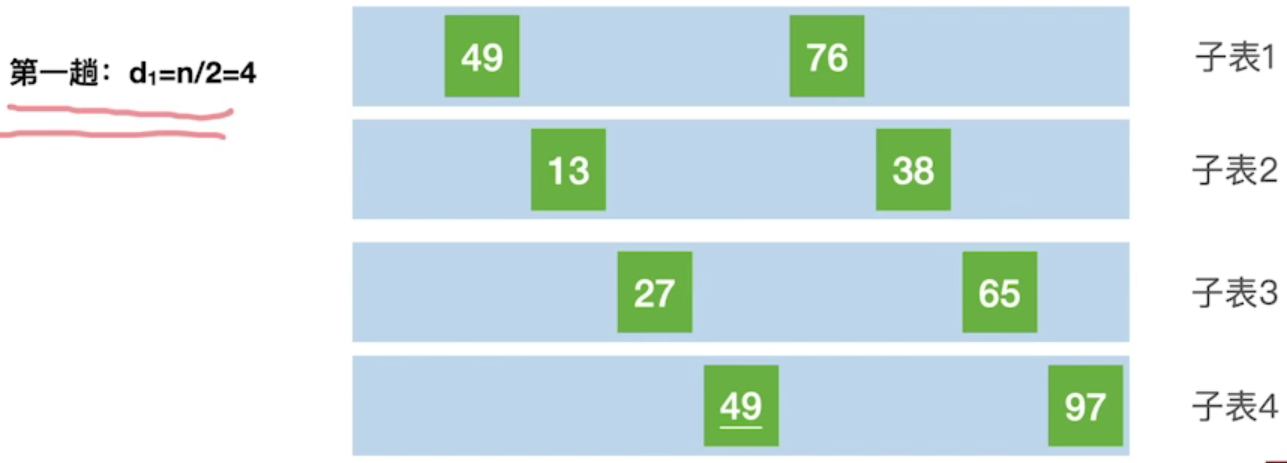


When sorting for the third time, the whole table has shown "basic order", and "direct insertion sorting" is performed for the whole again
code
void Shell_Sort(int a[],int n) //Hill incremental sort, no sentry
{
int i,j,d;
for(d = n/2;d>=1;d=d/2) //The increment decreases by a multiple of 2
{
for(i = d+1;i<=n;++i) //Insert sort the first number of default subsequences is ordered
{
if(a[i] < a[i-d]) //The first number of the current unordered sequence is smaller than the ordered sequence
{
a[0] = a[i];//Temporarily store the number to insert, not sentinels
for(j = i-d;j>0 && a[0]<a[j];j=j-d) //Move the element to make room for the number of inserts
{
a[j+d] = a[j];
}
a[j+d] = a[0];//At the end of the cycle, J has an offset d, so the correct position is to insert the number at j+d
}
}
}
}
performance analysis
Time complexity
It is related to the selection of incremental sequences d1,d2,d3... At present, it is impossible to prove the exact time complexity by mathematical means
Worst case O(n^ 2), when n is in a certain range, it can reach O(n^1.3)
Space complexity: O(1)
Stability: unstable

Applicability: only applicable to sequential list, not linked list
2, Bubble sorting
thinking
Compare the values of adjacent elements from back to front (or from front to back). If it is in reverse order (i.e. a [I-1] > a [i]), exchange them until the sequence comparison is completed. This process is called "one trip" bubble sorting.
Optimization: if no exchange occurs in a comparison, the whole sequence is orderly
code
void Bubble_Sort(int a[],int n) //Bubble sorting
{
for(int i=0;i<n-1;i++) //Each sort will swap the smallest element to the i position of the array
//The last number does not need to be sorted
{
bool f = false;//Is there an exchange
for(int j = n-1;j>i;j--) //Comparison and exchange from back to front
{
if(a[j] < a[j-1]) //Reverse order will be exchanged, and the same or no order will be exchanged to ensure stability
{
swap(a[j],a[j-1]);
f = true;
}
}
if(f == false) return; //If no exchange occurs, the whole sequence is orderly
}
}
performance analysis
Time complexity

Each exchange requires the element to be moved 3 times
Best case: O(n)
Worst case: O(n ^ 2)
Average: O(n ^ 2)
Space complexity: O(1)
Stability: stable
Applicability: applicable to sequence list and linked list
3, Quick sort
thinking
In the to be sorted table L[1... n], an element pivot is still taken as the pivot (benchmark). Usually, one-time sorting divides the to be sorted table into two independent parts L[1... k-1] and L[k+1... n], so that all elements in the left sequence are less than pivot and all elements in the right sequence are greater than or equal to pivot, then the pivot is placed on its final position L(k). This process is called "partition". Then repeat the above process recursively for the two sub tables respectively until there is only one element or empty in each part, that is, all elements are placed in their final position.
code
void qsort(int a[],int l,int r)
{
if(l>=r) return;
int i = l-1,j = r+1,pivot = a[(l+r)/2];
while(i<j)
{
do i++;while(a[i]<pivot);
do j--;while(a[j]>pivot);
if(i < j) swap(a[i],a[j]);
}
qsort(a,l,j);
qsort(a,j+1,r);
}
performance analysis
If the pivot selected each time divides the sequence to be sorted into two uniform parts, the recursive depth is the smallest and the algorithm efficiency is the highest
If the pivot selected each time divides the sequence to be sorted into two uneven parts, the recursion depth will increase and the efficiency of the algorithm will become low
If the initial sequence is in order or reverse order, the performance of fast row is the worst (because each pivot is selected as the edge element)
Time complexity
Best case: O(nlogn)
Worst case: O(n^2)
Spatial complexity
Best case: O(logn)
Worst case: O(n)
Stability: unstable

4, Simple selection sort
thinking
Find the smallest in each loop and exchange it with the number in front of the array
code
void select_sort(int a[],int n)
{
for(int i=0;i<n-1;i++)
{
int Min = i;
for(int j = i+1;j < n;j++)
{
if(a[j] < a[Min]) Min = j;
}
if(Min!=i) swap(a[i],a[Min]);
}
}
performance analysis
Time complexity
Best case: O(n^2)
Worst case: O(n^2)
Spatial complexity
O(1)
Stability: unstable
Applicability: sequence list, linked list
5, Heap sort
What is a pile?
If n keyword sequences L[1... N] satisfy one of the following properties, they are called heap:
1. If: L(i) ≥ L(2i) and L(i) ≥ L(2i+1)(1 ≤ i ≤ n/2) - large root pile
2. If: L(i) ≤ L(2i) and L(i) ≤ L(2i+1)(1 ≤ i ≤ n/2) - small root pile
Build large root heap
Idea: check all non terminal nodes to see if they meet the requirements of large root heap. If not, adjust them
Check whether the current node satisfies that the root is greater than or equal to the left and right. If not, swap the current node with a larger child (when creating a small root heap, swap the current node with a smaller child)
If the element exchange destroys the next level of heap, continue to adjust downward in the same way (small elements keep falling)
Insert element
For the small root heap, the new element is placed at the end of the table and compared with the parent node. If the new element is smaller than the parent node, the two will be exchanged. The new element rises all the way until it can't rise
Delete element
The deleted element is replaced by the element at the bottom of the heap, and then the element is allowed to fall continuously until it cannot fall
Sort based on heap
Each time, the top elements of the heap are added to the ordered subsequence (exchanged with the last element in the sequence to be sorted), and the sequence of elements to be sorted is adjusted to the large root heap again (small elements keep falling)
Efficiency analysis

Time complexity O(nlogn)
In the process of heap building, the keyword comparison times shall not exceed 4n, and the heap building time complexity = O(n)
Sorting time complexity = O(nlogn)
Space complexity O(1)
Space complexity = O(1)
Stability: unstable
6, Merge sort
Merging: merging two or more ordered sequences into one
N-way merging: N in 1. Each element selected needs to compare keywords n-1 times
code
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e5+10;
int a[N],tmp[N],n;
void merge_sort(int a[],int l,int r)
{
if(l>=r) return;//The number of interval elements is not greater than 1, and sorting is not required
int mid = l+r>>1;
merge_sort(a,l,mid),merge_sort(a,mid+1,r);//Split an interval in half
int i = l,j = mid+1,k = 0;
while(i<=mid && j<=r) //The combined two sequences must be ordered, and the double pointer algorithm is used for selection
{
if(a[i] <= a[j]) tmp[k++] = a[i++];
else tmp[k++] = a[j++];
}
while(i<=mid) tmp[k++] = a[i++];//The length of the two sequences may not be consistent, so add the rest to the temporary array
while(j<=r) tmp[k++] = a[j++];
for(int i=l,j=0;i<=r;i++,j++) //After sorting, assign the temporary array to the original array, and sort the interval [l,r]
{
a[i] = tmp[j];
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i];
}
merge_sort(a,0,n-1);
for(int i=0;i<n;i++)
{
cout<<a[i]<<" ";
}
return 0;
}
Efficiency analysis
Time complexity: O(nlogn)
N elements are sorted by 2-way merging. The number of merging times = log2 n. if the time complexity of each merging is O(n), the time complexity of the algorithm is O(nlogn)
Space complexity: O(n)
Stability: stable
7, Cardinality sort
thought
Suppose that the key of each node aj in a linear table with length n is composed of d tuples ()
Where 0 ≤ kj ≤ r-1, r is called "cardinality"
The descending sequence obtained by cardinality sorting is as follows:
Initialization: set r empty queues
"Allocate" and "collect" d keyword bits according to the order of increasing the weight of each keyword bit (number, ten and hundred)
Time complexity: O(d(n+r))
One time allocation O(n), one time collection O(r), a total of D times allocation and collection, total time complexity = O(d(n+r))
Space complexity: O(r)
Requires r secondary queues
Stability: stable
application
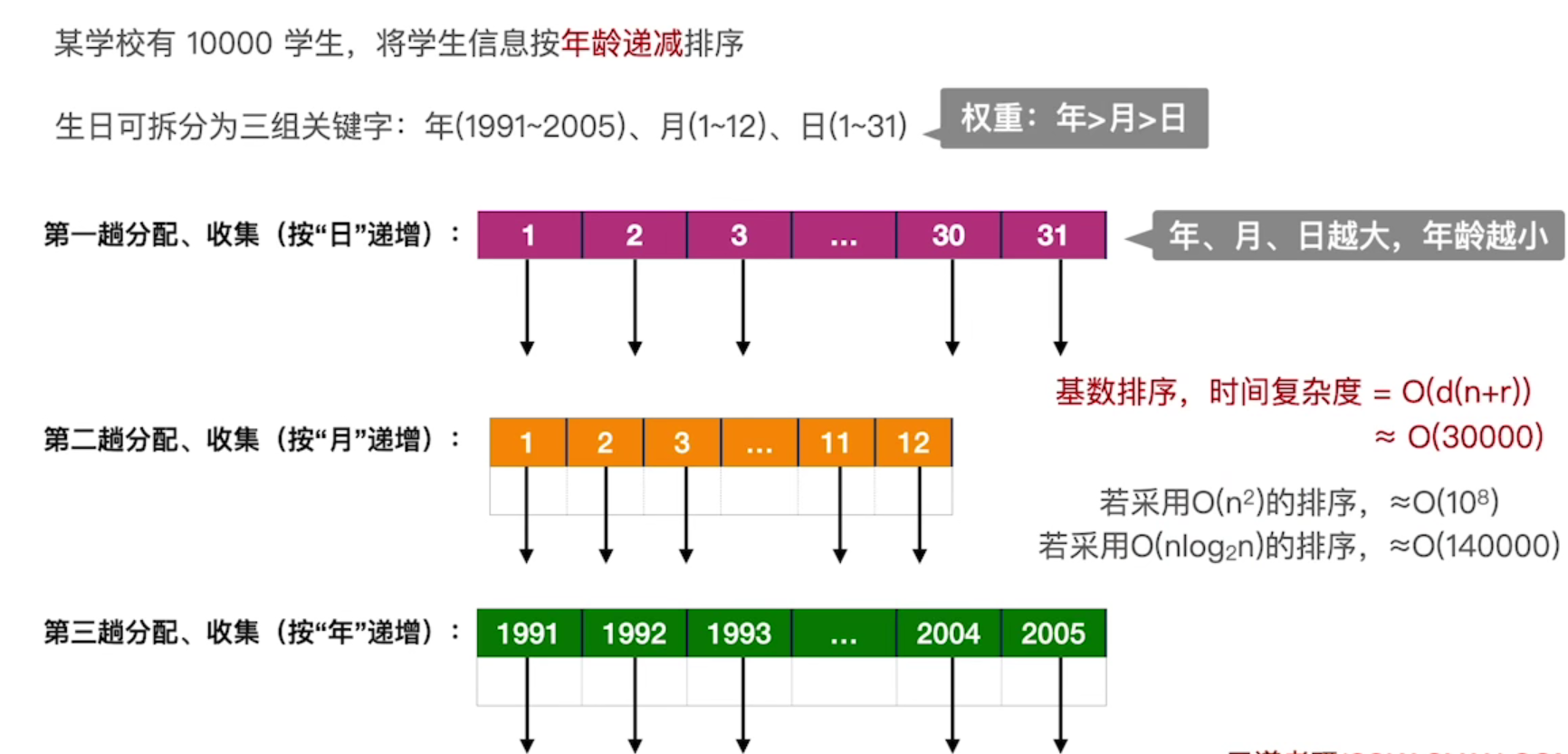
Cardinality sorting is good at solving the following problems:
① The number of data elements can be easily divided into d groups, and d is small
② The value range of each group of keywords is small, that is, r is small
③ The number of data elements n is large
8, External sorting
The disk is stored in "blocks", and the size of each block is 1KB
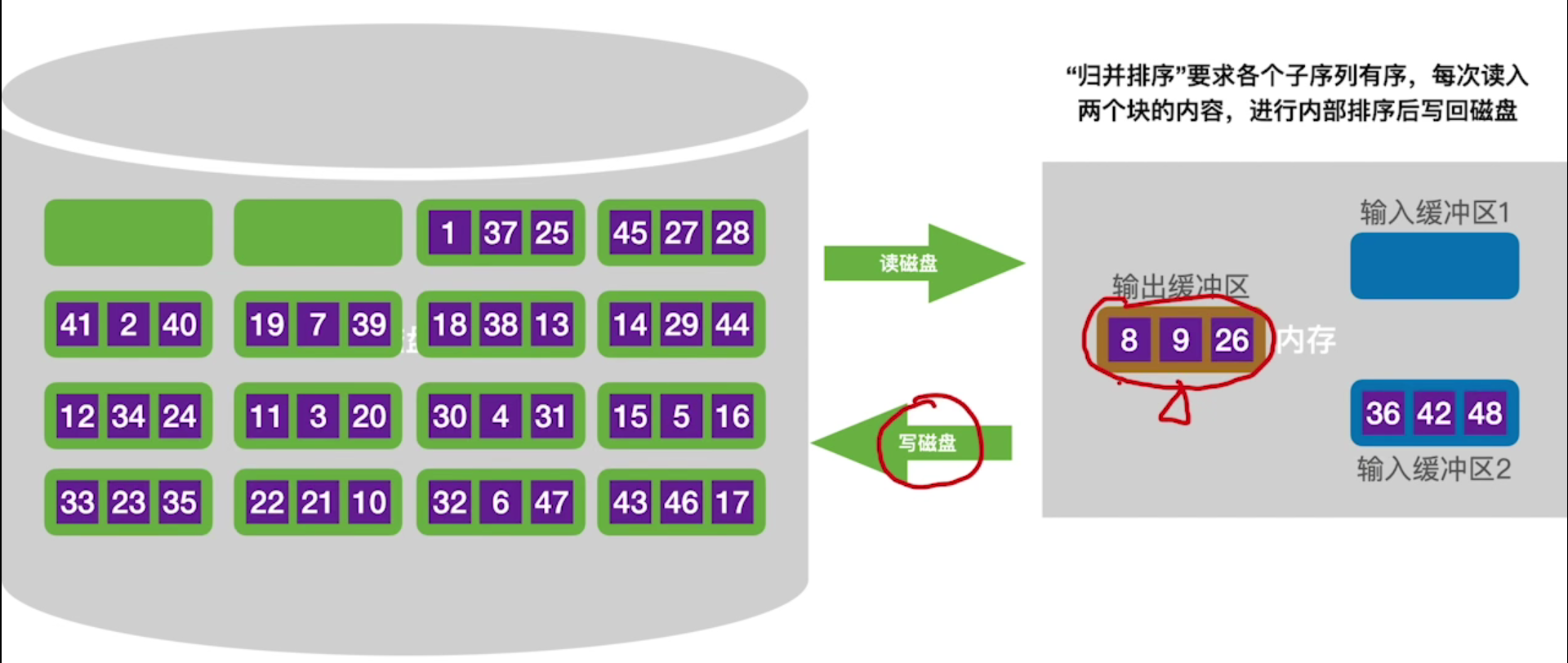
Read the data into memory, merge and sort it, and then write it to disk
Construct the initial merge block segment: 16 "read" and "write" operations are required
Knowledge sorting and summary
Simple selection sorting can take out the exchange position between the smallest (or largest) value in the current unordered sequence and the element in the first position.
A heap sort always selects a maximum value at the root node for each pass.
Bubble sorting always compares two to choose a maximum value in front of the array.
The pivot selected by quick sort is in its final position in one sort
The insertion sort (direct, bisection) is not necessarily in the final position, because it is uncertain whether the later inserted elements will affect the previous elements.
Hill sort (essentially insert sort) only inserts Sort directly into subsequence, so it cannot be determined.
Two way merge sort cannot determine the final position unless all sequences are put into the cache at one time (which is not worth the loss).
Therefore, after the trip, whether the sorting of an element in its final position can only be:
Simple selection sort, quick sort, bubble sort, heap sort