Summary

KMP (invented by Knuth,Morris,Pratt) algorithm with time complexity:
T = O ( n + m ) T=O(n+m) T=O(n+m)

Compared with violence-matched O(mn), there is a certain improvement.

The core idea of the KMP algorithm is that when a mismatch occurs, the longest prefix is found in the previously matched parts, such as the purple and green parts in the figure below, so that the next shift aligns the prefix directly to the back, so that you do not have to move only one bit at a time. The pointer in the string will not go back.

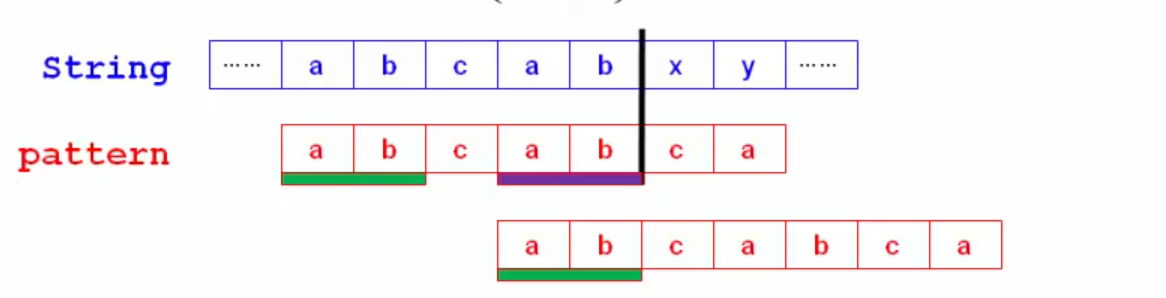
Construct match array

To know where we are going to fall back in the substring when a mismatch occurs, we need to do the following analysis for the pattern:

Define the match function to construct the next table:

m a t c h ( j ) = { full foot p 0 . . . p i = p j − i . . . p j Of most large i ( < j ) − 1 ， as fruit this kind Of i No Existing stay match(j)= \begin{cases} satisfies p_0...p_i=p_{j-i}...the maximum i(<j)\-1 of p_j if such I does not exist\end{cases} match(j) ={satisfies p0... pi = pj_i... Maximum I (<j) 1 of PJ if such I does not exist

For example:

match(j) is only related to a smaller pattern substring, which holds the information of the longest substring that can be matched one by one.

Save it in the match[] array.

Recursively, when calculating match[j], if pattern[match[j-1] + 1] == pattern[j], you can get match[j]=match[j-1]+1 directly.

If you are not so lucky as pattern [match[j-1] + 1]!= pattern[j], and don't want to go back to the starting point, you can find the matching part (the first green part below) forward according to the match value of match[j-1], then for the same last half, the last purple part and the first green part must match, then use the steps above.

The first question mark is match[match[j-1]+1], and the second is, of course, J.

KMP algorithm

With the match[] array, the implementation of the KMP algorithm is simple:

The Definitions s and p pointers iterate through the main string and the pattern string from the beginning, respectively, and loop as follows when neither reaches the end:

if (str[s] == pattern[p]), indicating that the current character matches and that s and P move backwards simultaneously;

Else if (p > 0), the current character is mismatched, either the 0th character of the pattern string or the trivial case in the following figure, you need to trace the P pointer back to the end of the green part, which is the match value of p-1: P = March [p-1] + 1.

Otherwise, the first character of the description pattern string does not match, ++;

code implementation

#include <stdlib.h>
#include <string.h>

void buildMatch(char const* pattern, int* match) {
    int prev = 0, j = 0;
    int m = strlen(pattern);
    match[0] = -1;
    for (j = 1; j < m; ++j) {
        prev = match[j - 1];
        while ((prev >= 0) && (pattern[prev + 1] != match[j])) {
            //i Keep going backwards
            prev = match[prev];
        }
        if (pattern[j] == pattern[prev + 1]) {
            //pattern[j]==pattern[match[j-1]+1]
            match[j] = prev + 1;
        } else {
            //No true substring to match
            match[j] = -1;
        }
    }
    return;
}

int KMP(char const* str, char const* pattern) {
    //Get the length O(n) of str
    int n = strlen(str);
    //Get the length O(m) of the pattern
    int m = strlen(pattern);
    int s = 0, p = 0;
    if (m > n)
        return -1;
    int* match = (int*)malloc(sizeof(int) * m);
    //Construct next table
    buildMatch(pattern, match);
    //None of them reached the end O(n), s never fell back
    while (s < n && p < m) {
        if (str[s] == pattern[p]) {
            //Current character match
            ++s;
            ++p;
        } else if (p > 0) {
            //Current character mismatch, jump to the end of the last small substring
            p = match[p - 1] + 1;
        } else {
            //The first character mismatches
            ++s;
        }
    }

    return (p == m) ? s - m : -1;
}

Test Code

void test_KMP() {
    printf("\n%s\n", __func__);
    char string[] = "This is a simple example";
    char pattern0[] = "simple";
    char pattern1[] = " isa";
    char pattern2[] = "Th";
    char pattern3[] = "e";
    char pattern4[] = "exam";
    char pattern5[] = "sample";
    char* patterns[6] = {pattern0, pattern1, pattern2, pattern3, pattern4, pattern5};
    int p;
    printf("\nstring:%s\n", string);
    for (int i = 0; i < 6; ++i) {
        printf("\npattern%d:%s\n", i, patterns[i]);
        p = KMP(string, patterns[i]);
        if (p != -1) {
            printf("%s\n", string + p);
        } else {
            printf("Not found\n");
        }
    }
    return;
}