1 overview of KMP algorithm

Recently, when writing leetcode28, I thought of KMP algorithm. I have seen this algorithm roughly before and searched a lot of information on the Internet, but I still can't understand it. Recently, I read it in detail again and finally found something. So make a record to facilitate your memory.
Problem Description:

 pat Represents a pattern string with a length of M，txt Represents a text string with a length of N. Please in txt Find substring in pat，If it exists, the starting index of this substring is returned; otherwise, it is returned -1. 

2 violence algorithm

If you want to understand the KMP algorithm, you must understand the violence algorithm. It is suggested that those who are not familiar with the violence algorithm should write the violence algorithm manually first, and then deeply understand the KMP. I won't repeat it here, but directly post the algorithm.

class Solution { 
public: 
    int strStr(string haystack, string needle) { 
        if(needle.length() == 0)
            return 0; 
        for(int i = 0; i < (int)(haystack.length() - needle.length() + 1); i++) {
            for(int j = 0; j < needle.length(); j++) { 
                if(haystack[i + j] != needle[j])
                    break; 
                if(j == needle.length() - 1)
                    return i; 
            } 
        } 
        return -1; 
    } 
};

The time complexity of the violence algorithm is O(m * n), because for each matching failure, we must match from scratch.

3 KMP algorithm

3.1 KMP algorithm

int strStr(string haystack, string needle) {
        int n = haystack.size(), m = needle.size();
        if (m == 0) {
            return 0;
        }
        vector<int> next(m);
        for (int i = 1, k = 0; i < m; i++) {
            while (k > 0 && needle[i] != needle[k]) {
                k = next[k - 1];
            }
            if (needle[i] == needle[k]) {
                k++;
            }
            next[i] = k;
        }
        for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && haystack[i] != needle[j]) {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;
    }

Author: LeetCode-Solution
 Link: https://leetcode-cn.com/problems/implement-strstr/solution/shi-xian-strstr-by-leetcode-solution-ds6y/
Source: force buckle( LeetCode)
The copyright belongs to the author. For commercial reprint, please contact the author for authorization. For non-commercial reprint, please indicate the source.

3.2 differences between KMP algorithm and violence algorithm

KMP algorithm is essentially the processing of pat string.
The violent algorithm never processes the pat string, so every time there is a mismatch, it needs to restart the matching from the beginning of the pat string, resulting in repeated operations (the previous matching is calculated again).
For example, when the txt string is "aabaaaaaaaac" and the pat string is "aabaaac", the i pointer points to the txt string and the j pointer points to the pat string. Let's match from scratch until the character pointed to by the i pointer is not equal to the character pointed to by the j pointer, as shown in Figure 1:

                                   Figure 1          

At this time, the violence algorithm will fallback the i pointer and the j pointer, point the i pointer to the second character of txt and the j pointer to the first character of pat, and start matching again.

The KMP algorithm never fallback the i pointer, but only the j pointer, as shown below:

So why can you go back like this?
Reason 1) as shown in Figure 1, at this time, i points to "b" and j points to "c", and the suffix "aa" of txt is exactly the same as the prefix "aa" of pat, so J can be fallback to "b".
According to this feature, we can traverse pat, and then find the longest length of each substring with the same prefix and suffix, that is, the next array, and then use this next array to traverse txt.

3.3 find the next array

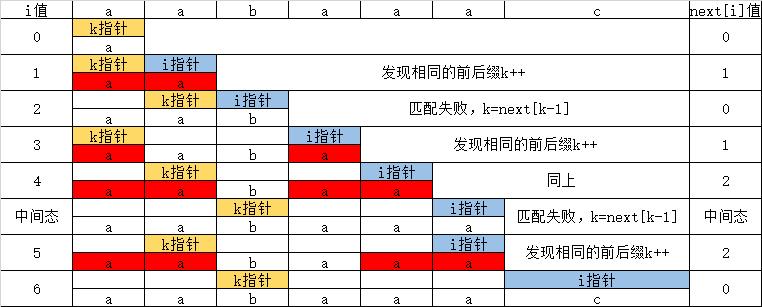
As shown in the figure above
If pat[k] == pat[i], then K + +, I + +, next[i] = k;.
If pat [k]= When pat [i], then k = next[k - 1], i remains unchanged until k == 0, I + +. K cannot simply go back to the initial position, as shown in the figure. When I is 5, the matching fails. If K directly returns to 0, then next[5] is equal to 1 and an error occurs.

3.4 matching string

After obtaining the next array, the next step is to match txt and pat. When txt and pat are mismatched, the next array is used for maximum displacement, as shown in the code.