Longest prefix

Give a string ABA

Prefix set: {a, ab, aba, abab}

Suffix set: {a, ba, aba, baba}

The equal pre suffix is the set element marked with the same color above. The longest pre suffix is the longest of all equal pre suffixes, that is, the aba above. Take pictures for example:

The prefix such as longest phase is the basis of KMP algorithm sliding. We use the next array to store the longest phase and other pre suffixes, so as to avoid the complexity of traversing and searching every time we need to use the longest phase and other pre suffixes.

next array

concept

next[i]=j means that the length of the longest prefix of the string before the subscript I is j. next[0]= -1 (there is no separate string processing in front).

a	b	a	b	a	c	d
next[0] = -1	next[1] = 0	next[2] = 0	next[3] = 1	next[4] = 2	next[5] = 3	next[6] = 0

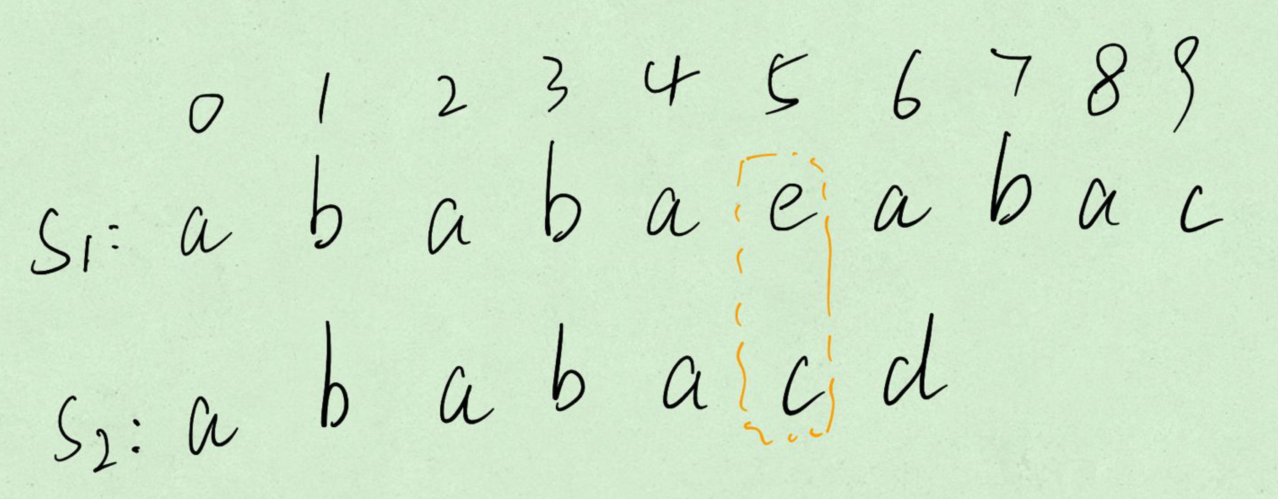
When s1[5]= When s2 [5], move s2 so that the prefix (ababa) of s2 matches the suffix (ababa) of s1, that is, compare s1[5] and s2[next[5]. The moving distance is the number of characters between the mismatched position subscript and the equal prefix, that is, 5-3 = 2.

As can be seen from the above example, next has two functions:

1. Subscript indicating the character that should be traced back when there is a character mismatch.
2. As mentioned above: the longest length of the string before subscript i is equal to the length of the previous suffix.

code implementation

class Solution {

public:
	void GetNext(const string& s, vector<int>& next) {
		int i = 0, j = -1;
		next[0] = -1; // There is no string before the character with subscript 0
		while (i < next.size() - 1) { 
			// Because each time I + + is assigned to the function body, then next[i] is assigned
			// Therefore, i needs to be less than next Size () - 1 to ensure that the self increment does not exceed the limit
			if (j == -1 || s[i] == s[j]) {
				i++;
				j++; 
				/* About j */
				/*
				s[i] == s[j]When established, next[i] is + 1 based on the value (j) of next[i - 1]
				In other words, it means that the length of the previous suffix is equal to + 1, and the prefix corresponding to the end of the new suffix i+1 is j+1
				*/
				/* 
				j == -1 When it is established, it indicates that there is no equal pre suffix,
				Therefore, the equal pre suffix length of the string before I is next[i] = (-1)++ = 0 
				*/ 
				next[i] = j;
			}
			else {
				j = next[j];
				// next[j] is the backtracking position. It is the length of the prefix such as the longest phase of the string before the character pointed to by j
				// In order to move the prefix to the position of the suffix, it is assumed that the equal length is m
				// Equivalent to (0, j-m), (1, J-M + 1) (m-1, J-1) matching up
				// for instance:
				// String: a B a C D
				// next:   -1 0 0 1 2 3
				//                j   i
				// Since the length of the prefix such as the longest phase of the string aba before the character b pointed to by j is 1,
				// Subscript 1 as a new j matches (0, j-1)
				// In other words, we only need to take subscript 1 as a new j to convert the pre suffix problem such as finding the longest phase of ababac into
				// The problem of finding the prefix such as the longest phase of abac.
			}
		}
	}

	void getNext(const string& pattern, vector<int>& next){ // Another way of writing
		int i, j = 0;
		next[0] = -1;   //There is no data in the first position, which is - 1
		for (int i = 1; i < next.size(); i++)
		{
			//If there is no matching prefix in the current position, the longest matching prefix of the current suffix is traced back
			while (j != 0 && pattern[j] != pattern[i])
			{
				j = next[j];
			}
			//If the position matches, add one to the next array based on the previous position
			if (pattern[j] == pattern[i])
			{
				j++;
			}
			next[i] = j;
		}
	}
};

As for the other writing method mentioned, there is no more analysis here. You can read it Ling Huan's blog.

Figure backtracking in GetNext

Take an intuitive example:

• The red parts are: the longest appearance, etc.

• The blue part is the element to be matched pointed by the double pointer.

• The black part is the part that does not start matching.

• The green part is the next array.
  

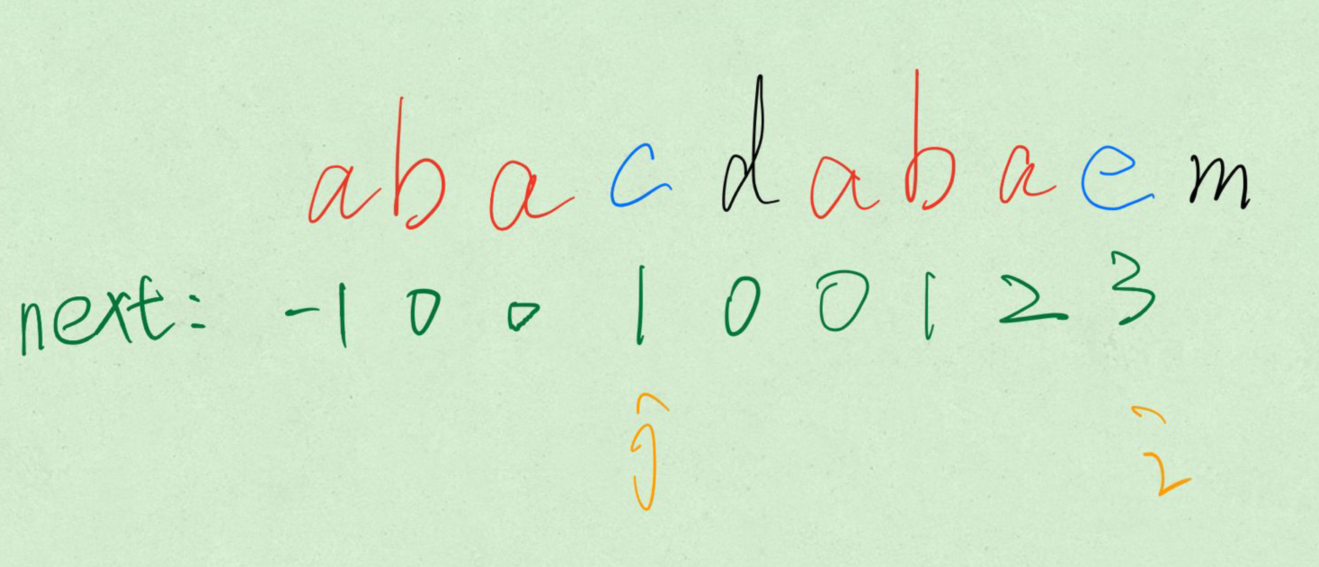
• If s[i] == s[j], the double pointer moves back at the same time, and the red area becomes larger.

• If there is no match, the equal pre suffix must be found again in the red part, and the length of the new equal pre suffix must be shortened.

The purple part is the longest prefix of the red part. It can be seen that the four purple parts are completely equal. At the same time, change the direction of J. after backtracking, j = next[j]:

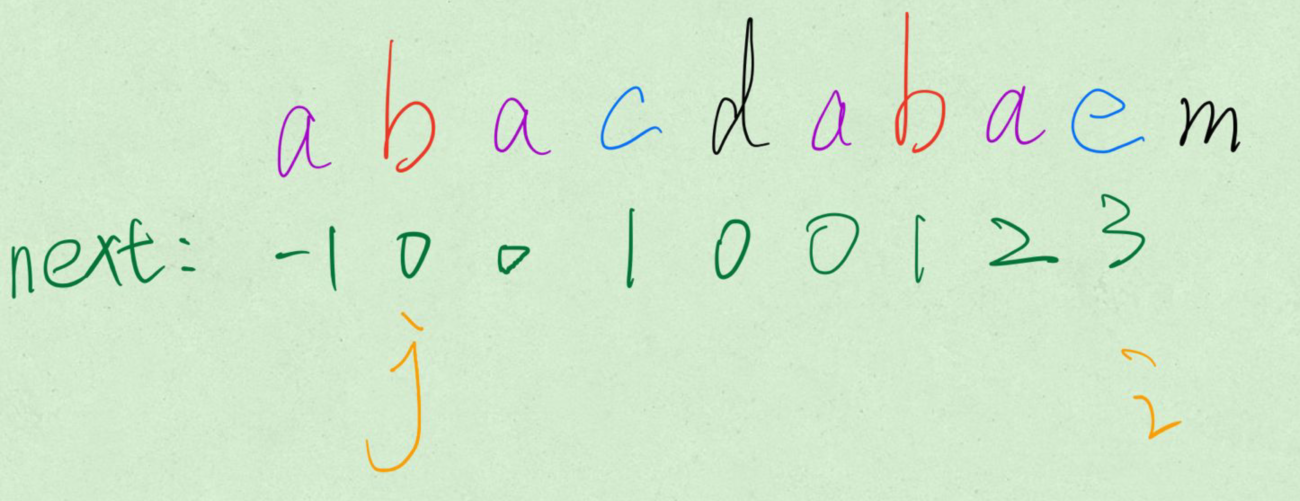
1. At this time, if s[i] == s[j], because the purple part in front of j is completely equal to the purple part in front of I. Then the length of the prefix of the longest phase is + 1.
2. If not, the next backtracking will be carried out. During the next backtracking in the figure, there is no equal pre suffix, so there is no purple part. Keep backtracking until J points to - 1. At this time, trigger the determination condition and execute j++; i++; next[i]=j; .

code

class Solution {
public:
	void GetNext(const string& s, vector<int>& next) {
		int i = 0, j = -1;
		next[0] = -1; // There is no string before the character with subscript 0
		while (i < next.size() - 1) { 
			if (j == -1 || s[i] == s[j]) {
				i++;
				j++; 
				next[i] = j;
			}
			else {
				// If there is no matching prefix in the current position, the longest matching prefix of the current suffix is traced back
				j = next[j];
			}
		}
	}

	int knuthMorrisPratt(const string& query, const string& pattern) {
		//If the condition is not met, false is returned directly
		if (query.empty() || pattern.empty() || query.size() < pattern.size())
		{
			return -1;
		}

		int i = 0, j = 0;
		int len1 = query.size(), len2 = pattern.size();
		vector<int> next(pattern.size(), -1); // next array
		GetNext(pattern, next);

		while (i < len1 && j < len2)
		{
			if (j == -1 || query[i] == pattern[j])
			{
				i++;
				j++; // i. j add 1 each
			}
			else j = next[j]; // i invariant, j backtracking
		}

		if (j == len2)
			return(i - len2); // Returns the first character subscript of the matching pattern string
		else
			return -1; // Return mismatch flag
	}
};

Complexity analysis

• Space complexity O(M): a next array with the length of M M M， M M M is the length of the mode string.
• Time complexity O(N + M): the time complexity mainly includes two parts: the construction of next array and the traversal of main string: the time complexity of the construction of next array is O(M); In the later matching, the main string is not backtracked, and the cycle time complexity is O(N), so the time complexity of KMP algorithm is O(N + M).