KMP algorithm: six steps to complete KMP

1. What is KMP

KMP algorithm is jointly proposed by D.E.Knuth, J,H,Morris and V.R.Pratt. It is called Knuth morria Pratt algorithm, or KMP template matching algorithm for short. Compared with brute force (brute force) algorithm, this algorithm has a great improvement, mainly eliminating the backtracking of the main string pointer and improving the time efficiency. (space for time)

2.KMP and naive template matching (brute force)

Brute force

This is super simple traversal comparison one by one....
Given string S,T,
Compare the first length of T and S with the same string of T, and the first index matching will be returned after success
Unsuccessful, continue to match the next string of S with the same length as T
... Iterate through each string of the same length as T, and match
This time complexity is O(n*m).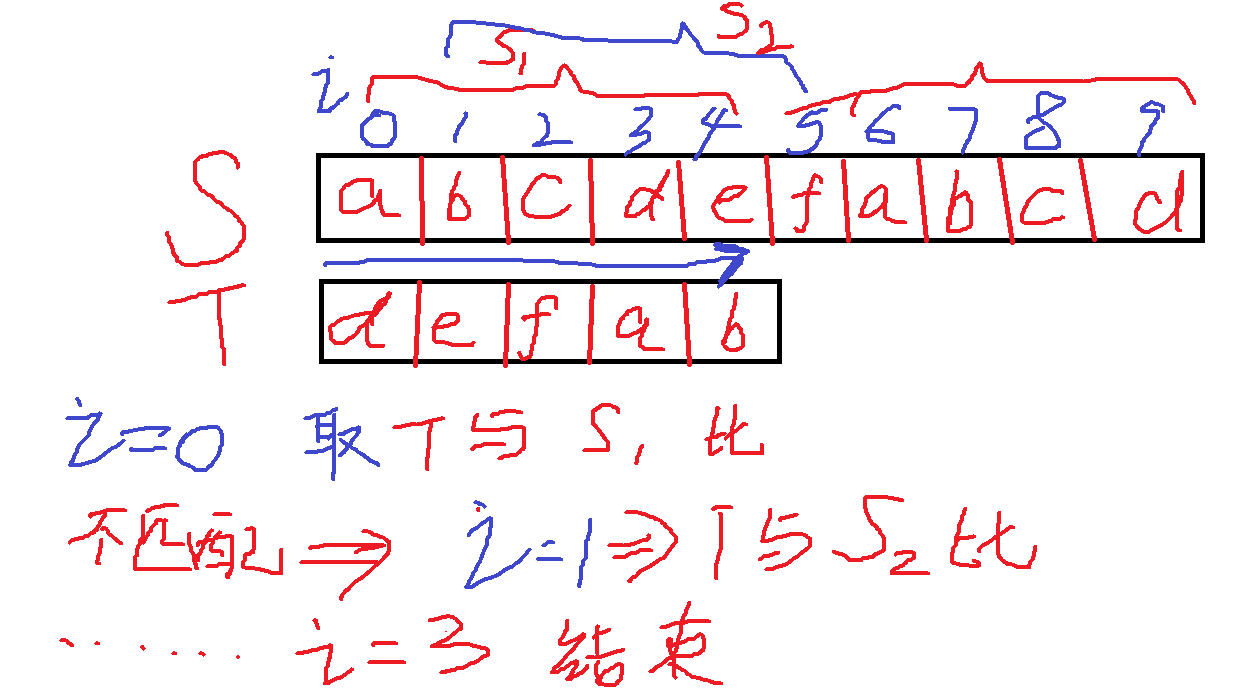

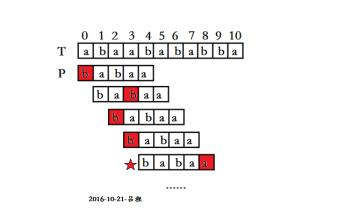
KMP template matching algorithm -- can achieve complexity O(m+n)

Step 1: first understand what is Prefix suffix string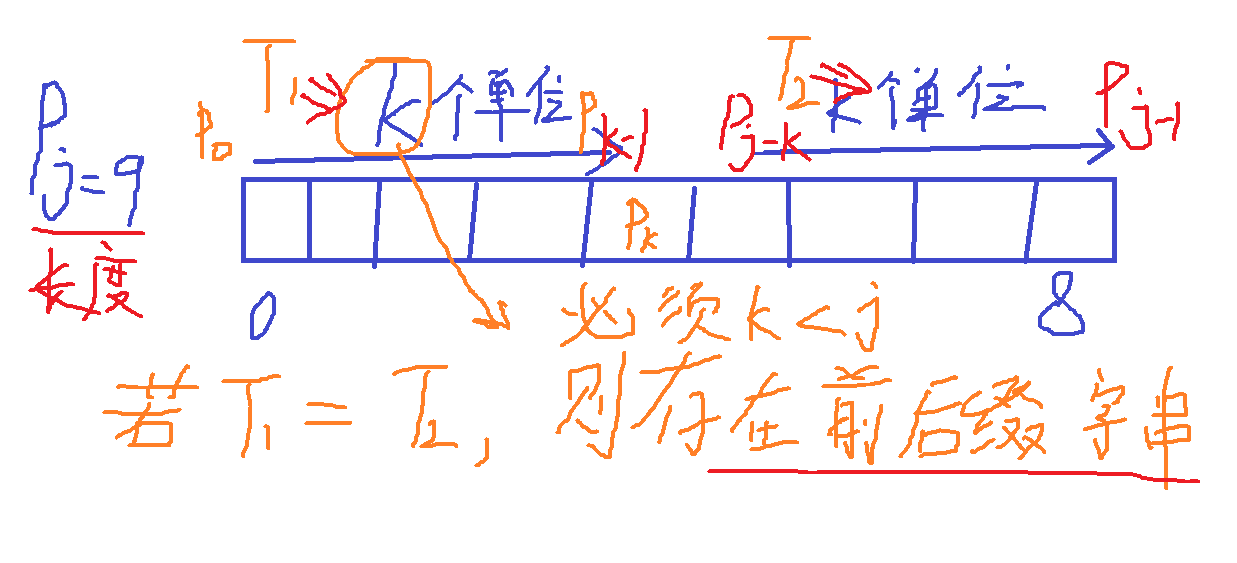
For example:
abcjkdabc, then the longest prefix and the longest suffix of this array are the same - it must be abc.
cbcbc, the longest prefix is the same as the longest suffix - cbc.
abcbc, the longest prefix and the longest suffix are the same, they do not exist.
Note the longest prefix: it starts with the first character, but does not contain the last character.

The second step is to understand the rules of string matching
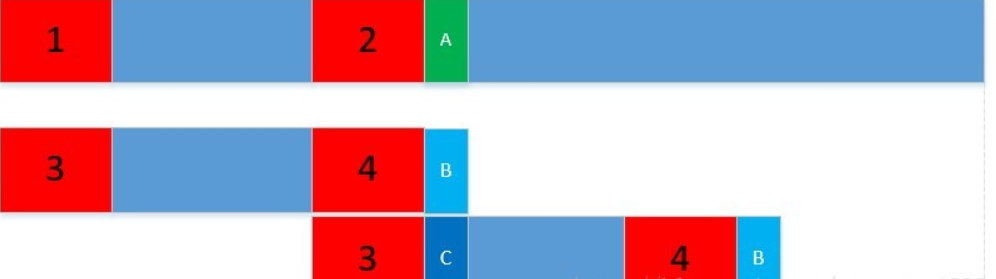
Suppose S and T are matched, and the matching rules are as shown in the figure

Here aba is the longest prefix string, and then next a is the longest prefix string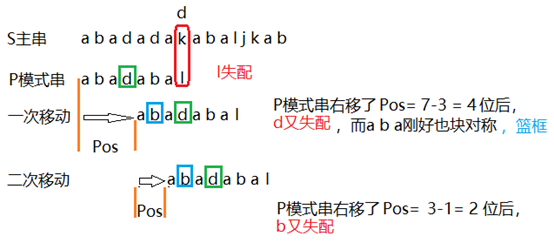

Sketch map of borrowing others:

The third step, how to get the update rule of j -- calculating the next array
I saw the fourth edition of data structure (java) and talked about it very well.
Formula:
Example demonstration: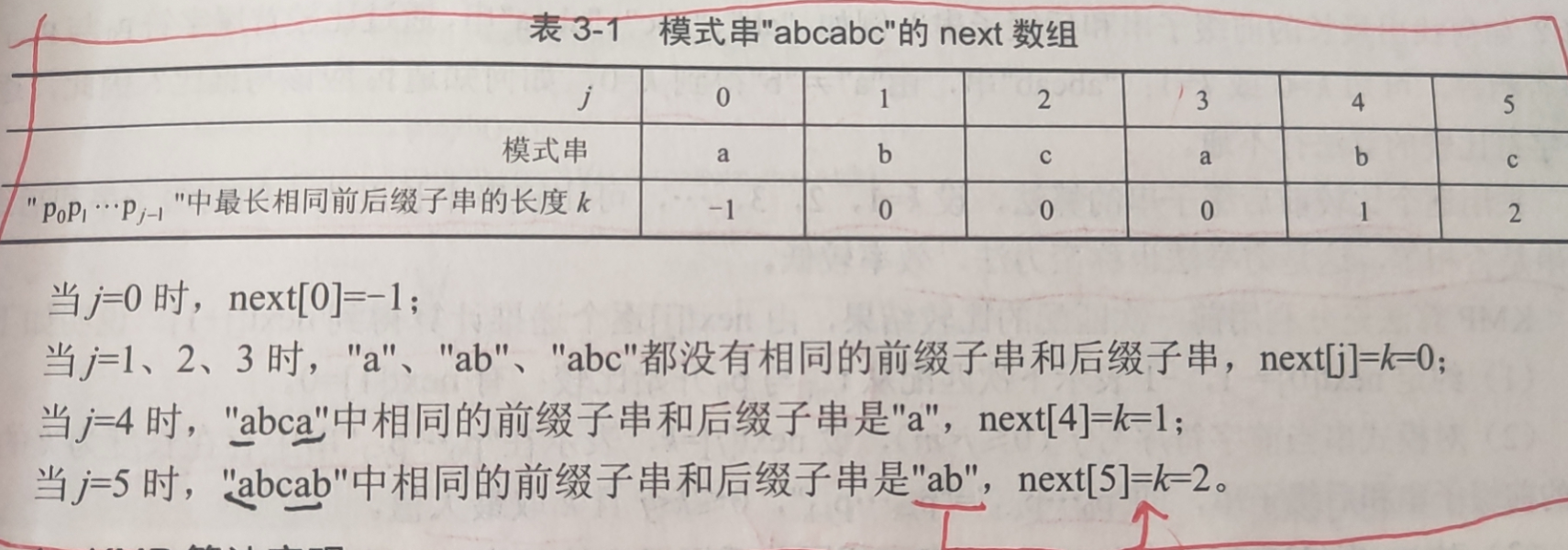

Step 4: calculate the code of next array on

int get_next(string t,int * next) {
    //Define an array first
    int length = t.length();
    int j=0,k=-1;
    next[0] = -1;
    while(j<length-1)//Because we are looking for the longest prefix string, we have to subtract one here.
        if(k==-1||t[j]==t[k]) { //The latest character of the current string is equal or the total length of the string is 1
            k++;
            j++;//Compare next character
            next[j] = k;//The longest prefix string is recorded, because the preceding k, j are all added with 1

        } else
            k = next[k];//Find the longest prefix string of the current j-length string again in the k-length prefix string, and update the index. It's said that this is the most difficult to understand
    return 1;
}

Step 5: understand that k = next[k]
k = next[k]; / / find the longest prefix string of the current j-length string in the k-length prefix string again,
I'll show you an example here, but I've understood it all at once.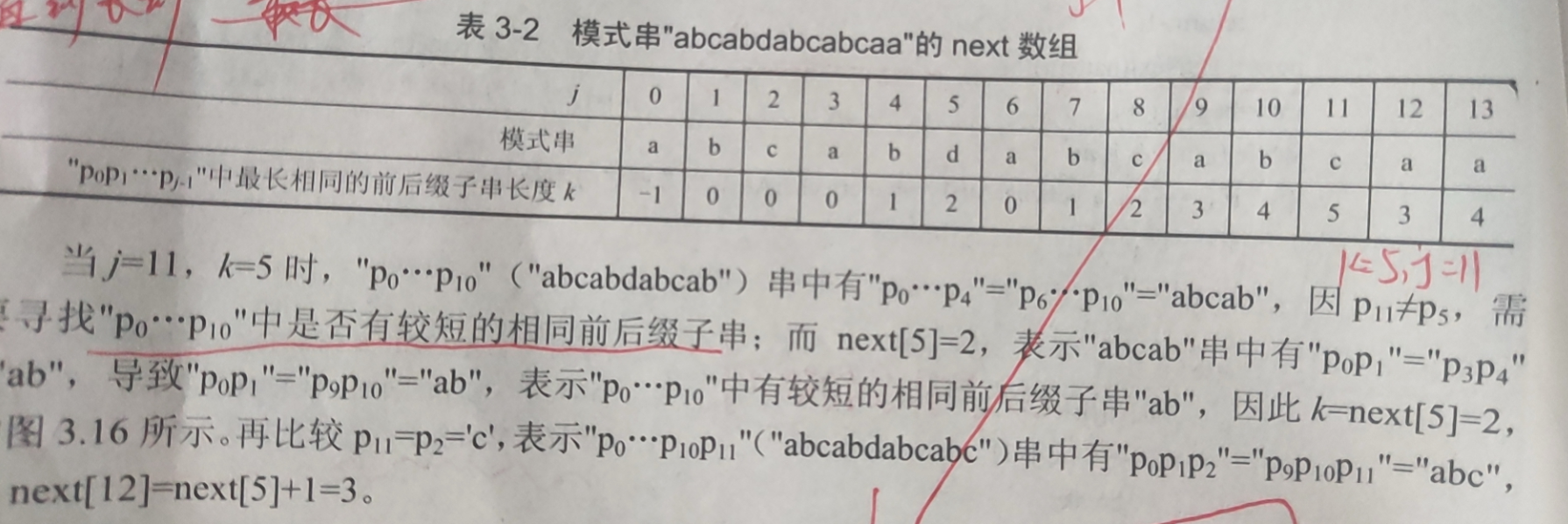

Figure: because p5!=p11, at this time, the longest prefix string will certainly not be larger than the last one, it can't be 6, we can only search again, and the rule of searching again is k = next[k]=2

Step 6, last step, match string code on

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
using namespace std;
//establishnextarray
int get_next(string t,int * next) {
    //Define an array first
    int length = t.length();
    int j=0,k=-1;
    next[0] = -1;//This is for
    while(j<length-1)//Because we are looking for the longest prefix string, we have to subtract one here.
        if(k==-1||t[j]==t[k]) { //The latest character of the current string is equal or the total length of the string1
            k++;
            j++;//Compare next character
            next[j] = k;//The longest prefix string is recorded

        } else
            k = next[k];//Re in k Prefix string of length find current j Longest prefix string of length string, update index
    return 1;
}
int compare_str(string s,string t,int pos) {
    int n=s.length();
    int m = t.length();
    if(n<m||pos>=n||n==0) { //Unreasonable input
        return 0;
    }
    if(pos<=0) {
        pos=0;//Improve fault tolerance
    }
    int next[m];
    //generatenextarray
    get_next(t,next);
    int i=pos,j=0;
    while(i<n&&j<m)
        if(j==-1||s[i]==t[j]) { //Current match succeeded, continue to match next character
            i++;
            j++;
        } else { //i No backtracking, matching rules update matching j
            j = next[j];//This is what we call the matching rule
            if(n-i+1<m-j+1)//Not enough strings left t No need to compare
                break;
        }

    if(j==m)
        return i-j;//Match succeeded. , return the corresponding index
    return -1;//Otherwise quit

}
int main() {
    string t,s;
    cin>>s;
    cin>>t;
    int pos =compare_str(s,t,0);
    cout<<pos;
    return 0;
}

Update and improve KMP algorithm.

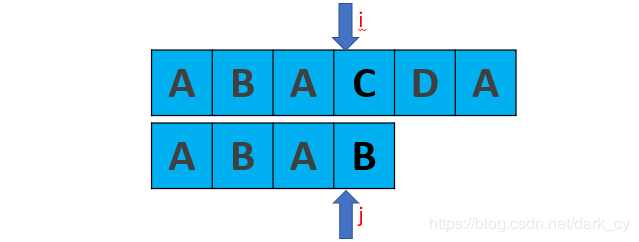
Now we're comparing C and B. they don't match.
Obviously, when our algorithm above gets the next array, it should be [- 1, 0, 0, 1]
So next[3] = 1. Next step matching: obviously we will compare C and B again, which is redundant
So we should improve the calculation of next array matching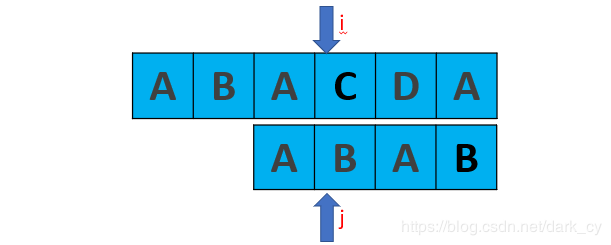

The improved algorithm is to avoid this situation, code demonstration

int get_next(string t,int * next) {
    //Define an array first
    int length = t.length();
    int j=0,k=-1;
    next[0] = -1;
    while(j<length-1)//Because we are looking for the longest prefix string, we have to subtract one here.
        if(k==-1||t[j]==t[k]) { //The latest character of the current string is equal or the total length of the string1
            k++;
            j++;//Compare next character
            //Using the improved algorithm
            if(t[j]!=t[k])
                next[j] = k;//The longest prefix string is recorded
            else next[j] = next[k];//Skip directly to the suffix string found last time, end of improved code

        } else
            k = next[k];//Re innext[k]Prefix string of length find current j Longest prefix string of length string, update index
    return 1;
}

Reference blog
https://blog.csdn.net/dark_cy/article/details/88698736:
https://blog.csdn.net/starstar1992/article/details/54913261?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task