preface
For the original knapsack problem and its optimization, please refer to this blog
knapsack problem
Initialization of knapsack problem
There are three general problems

Corresponding initialization method

- For volume up to j, f [ 0 ] [ j ] f[0][j] f[0][j] indicates that there is no item selected, and the volume is j at most. Therefore, it is set to 0. For the cycle, we are j at most. If V < 0, it means V1 > J, which does not exist.
- For a volume that is exactly j, f [ 0 ] [ j ] f[0][j] f[0][j] indicates that none of the items is selected, and the maximum volume is j, only f [ 0 ] [ 0 ] f[0][0] f[0][0] exists, and the rest do not exist. Therefore, it is set as an illegal number. As for whether it is positive infinity or negative infinity, it depends on whether the problem is to find the maximum or minimum; The reason for the loop boundary is the same as above
- The initialization condition is the same as the second one; For cyclic conditions, we are at least j, so they exist when V < 0, and their values are the values when v = 0.
01 Backpack
Packing problem
Personal problem solving ideas:
This problem is to make the remaining space of the backpack as small as possible, that is, the volume of the items put in should be as large as possible, because the items only give the volume and have no value, so we may equate the value of each item with its volume, so this is transformed into 01 backpack problem. So this d p [ i ] dp[i] dp[i] indicates that the total volume does not exceed the maximum volume under the backpack capacity, that is, the remaining volume is the smallest.
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 35 , M = 20010;
int n , m ;
int w[N] , v[N] ,f[M];
int main(){
cin>>m>>n;
for(int i = 1 ; i <= n ; ++i)cin>>w[i] ;
for(int i = 1; i <= n ; ++i)
for(int j = m ; j >= w[i] ; --j)
f[j] = max(f[j] , f[j-w[i]] + w[i]);
cout<<m - f[m]<<endl;
return 0;
}
Collection of pet elves
Problem solving ideas:
This problem has changed from single cost to two-dimensional cost. Our cost includes the number and physical strength of ELF balls, so we define two-dimensional dp;
d
p
[
i
]
[
j
]
[
k
]
dp[i][j][k]
dp[i][j][k] refers to the maximum number of ELF balls with no more than j and no more than k when considering the first I elves. From the knapsack problem, we can omit the first dimensional space and traverse it in reverse order. For two-dimensional, we still have
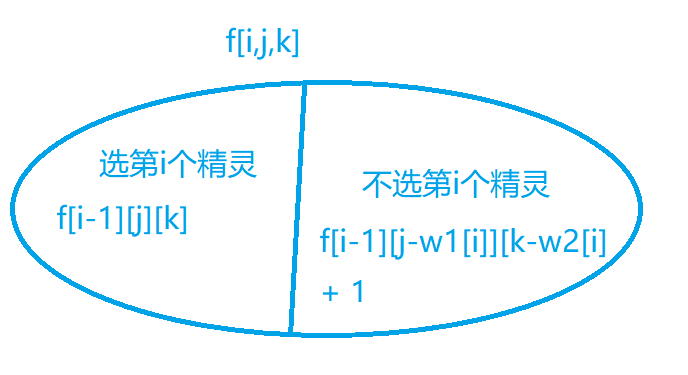
For the remaining physical strength, we are f [ N ] [ 1 − M ] f[N][1-M] f[N][1 − M] is equal to f [ N ] [ M ] f[N][M] The minimum physical strength of f[N][M], which is the minimum physical strength spent. At the same time, because our physical strength can't be 0, we will lose another 1
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110 , M = 1010;
int n , m , K;
int w[N] , v[N] ,f[M][M] ;
int main(){
cin>>m>>K>>n;
for(int i = 1; i <= n ; ++i)cin>>w[i]>>v[i];
for(int i = 1 ; i <= n ; ++i)
for(int j = m ; j >= w[i]; --j)
for(int k = K ; k > v[i] ; --k )
f[j][k] = max(f[j][k] ,f[j-w[i]][k-v[i]] + 1);
cout<<f[m][K]<<' ';
int cnt = 0;
for(int k = 1 ; k <= K ; ++k)
if(f[m][k] == f[m][K]){
cnt = k - 1;
break;
}
cout<<K - cnt <<endl;
return 0;
}
Digital combination
Problem solving ideas;
This is a typical 0 / 1 knapsack model. N positive integers are n items, and M is the volume of the knapsack. When the outer layer circulates to i (indicating the selection from the previous i numbers), Let F[j] indicate how many schemes "and is j". In the specific implementation, we only need to change the function of max in the original code to sum.
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 110 , M = 10010;
int n , m ;
int w[N] , f[M];
int main(){
cin>>n>>m;
for(int i = 1; i <= n ; ++i)cin>>w[i];
f[0] = 1;
for(int i = 1; i <= n ; ++i)
for(int j = m; j >= w[i] ; --j)
f[j] += f[j-w[i]];
cout<<f[m]<<endl;
return 0;
}
Happy Jin Ming
Problem solving ideas:
In this question, we can regard the money of each item as the volume, and the value of the item is the amount * importance. In this way, we become the 01 knapsack problem
code;
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 50010;
int n , m;
int f[N];
int main(){
cin>>m>>n;
for(int i = 1 ; i <= n ; ++i){
int w , v;
cin>>w>>v;
v *= w;
for(int j = m ; j >= w ; --j)
f[j] = max(f[j] ,f[j-w] + v);
}
cout<<f[m]<<endl;
return 0;
}
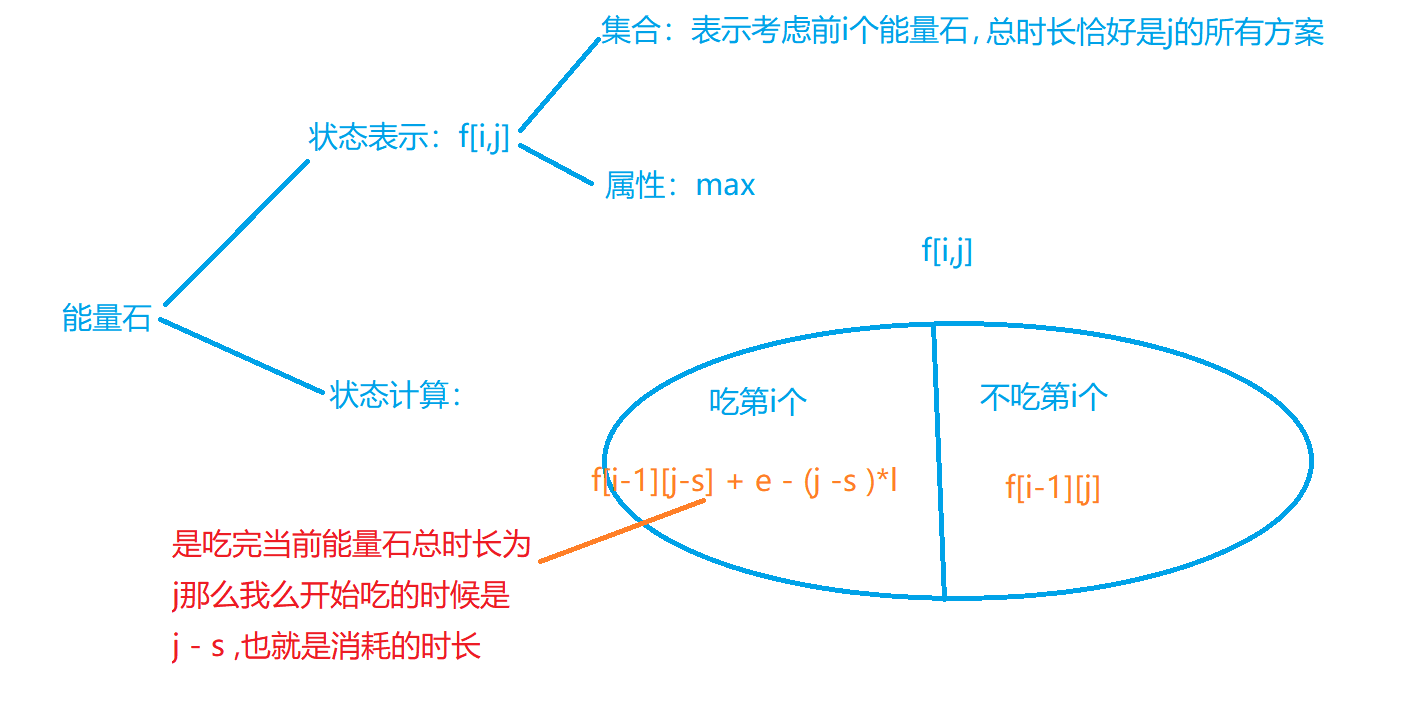
01 Backpack + greed
Problem solving ideas:
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 10010;
int n , m ;
int f[N];
struct Stone{
int s , e ,l;
bool operator < (const Stone & w)const {
return s * w.l < w.s * l;
}
}stone[N];
int main(){
int T;
cin>>T;
for(int C = 1 ; C <= T ; ++C){
m = 0;
cin>>n;
for(int i = 0 ; i < n ; ++i){
int s ,e ,l;
cin >>s>>e>>l;
stone[i] = {s ,e,l};
m += s;
}
sort(stone , stone + n);
memset(f , -0x3f , sizeof f);
f[0] = 0;
for(int i = 0 ; i < n ; ++i){
int s = stone[i].s , e = stone[i].e , l = stone[i].l;
for(int j = m ; j >= s ; --j)
f[j] = max(f[j] , f[j-s] + e - (j - s)*l);
}
int res = 0;
for(int i = 0 ; i <= m ; ++i)res = max(res , f[i]);
cout<<"Case #"<<C<<": "<<res<<endl;
}
return 0;
}
Number of solutions to knapsack problem
Monetary system
Problem solving ideas:
The difference between this question and the above number combination is that the number combination is that each number can only be selected once, and here each currency can be selected multiple times. Therefore, this is a complete knapsack template question. In the specific implementation, you only need to change the function of max in the original code to sum.
code:
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 20 , M = 3010;
int n , m;
int w[N] ;
LL f[M];
int main(){
cin>>n>>m;
for(int i = 1 ; i <= n ; ++i)cin>>w[i];
f[0] = 1;
for(int i = 1; i <= n ; ++i)
for(int j = w[i] ; j <= m ; ++j)
f[j] += f[j-w[i]];
cout<<f[m]<<endl;
return 0;
}
Monetary system II
Problem solving ideas;
Equivalence classes have the following three properties:,

Therefore, we need to consider whether each a[i] query will be composed of other numbers in a that do not contain it. If not, we need to select it. If we can, we need not select it. So how do you know? Then this is the same problem as the previous one. After we deal with it, for each a[i] if its
f
[
a
[
i
]
]
!
=
1
f[a[i]]!=1
f[a[i]]!=1 then it means that this number cannot be composed of other numbers
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110 , M = 25010;
int n , m ;
int f[M] , w[N];
int main(){
int T;
cin>>T;
while(T--){
cin>>n;
memset(f , 0 , sizeof f);
f[0] = 1;
for(int i = 1 ;i <= n ; ++i){
cin>>w[i];
for(int j = w[i] ; j <= M ; ++j)
f[j] += f[j-w[i]];
}
int cnt = 0;
for(int i = 1; i <= n ;++i)
if(f[w[i]] == 1)cnt++;
cout<<cnt<<endl;
}
return 0;
}
Multiple knapsack problem
Celebration party
Problem solving ideas:
We regard the appropriation amount as the volume of the backpack, the price as the volume of the goods, and the value as the value of the goods. Then this topic is a bare topic of multiple backpacks. For this data range, we can use binary optimized multiple knapsack to solve it.
Detailed explanation of multiple backpacks
code:
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 510 , M = 6010;
int n , m;
int f[M];
struct Good{
int w , v;
};
vector<Good>goods;
int main()
{
cin>>n>>m;
for(int i = 1; i <= n ; ++i)
{
int w ,v , s;
cin>>w>>v>>s;
for(int k = 1 ; k <= s; k *= 2){
s -= k;
goods.push_back({k*w,k*v});
}
if(s > 0)goods.push_back({s*w,s*v});
}
for(auto good : goods)
for(int j = m ; j >= good.w ; --j)
f[j] = max(f[j] ,f[j-good.w] + good.v);
cout<<f[m]<<endl;
return 0;
}
Hybrid knapsack problem
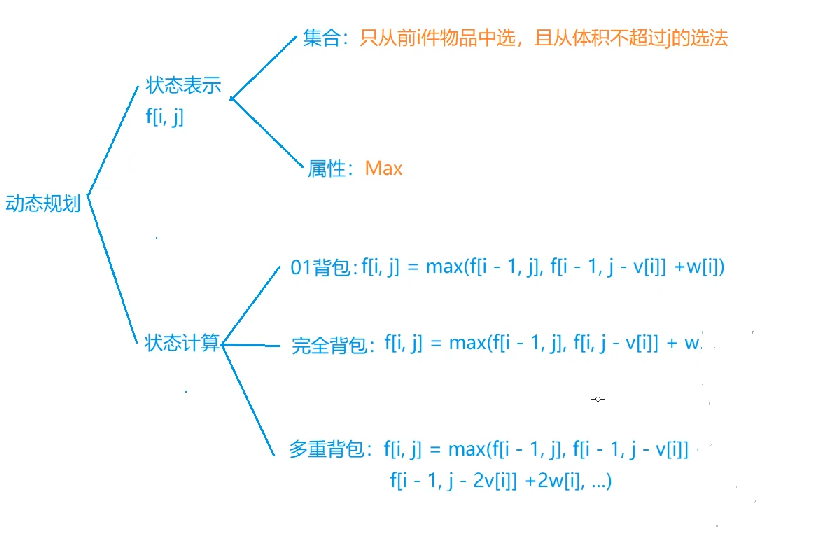
Problem solving ideas:
Let's review the expression of knapsack problem: d p [ i ] [ j ] dp[i][j] dp[i][j] represents the maximum value of the first I items whose total volume does not exceed j. We found that it has no limit on the type of goods. For different types of items, we only calculate the state differently. At the same time, for the i-th item, we will only consider the i-th item instead of the first i-1 item. Therefore, for this problem, we calculate the corresponding state of the ith item according to its type.
code:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n , m;
int f[N];
int main(){
cin>>n>>m;
for(int i = 1 ; i <= n ; ++i)
{
int v , w ,s;
cin>>w>>v>>s;
if(s == 0)// Complete Backpack
{
for(int j = w ; j <= m ; ++j)f[j] = max(f[j] ,f[j-w] + v);
}else{
if(s == -1)s = 1;
for(int k = 1 ; k <= s ; k *= 2){
s -= k;
for(int j = m ; j >= k * w ; --j)f[j] = max(f[j] , f[j-k*w] + k*v);
}
if(s)
for(int j = m ; j >= s*w ; --j)f[j] = max(f[j] , f[j-s*w] + s*v);
}
}
cout<<f[m]<<endl;
return 0;
}
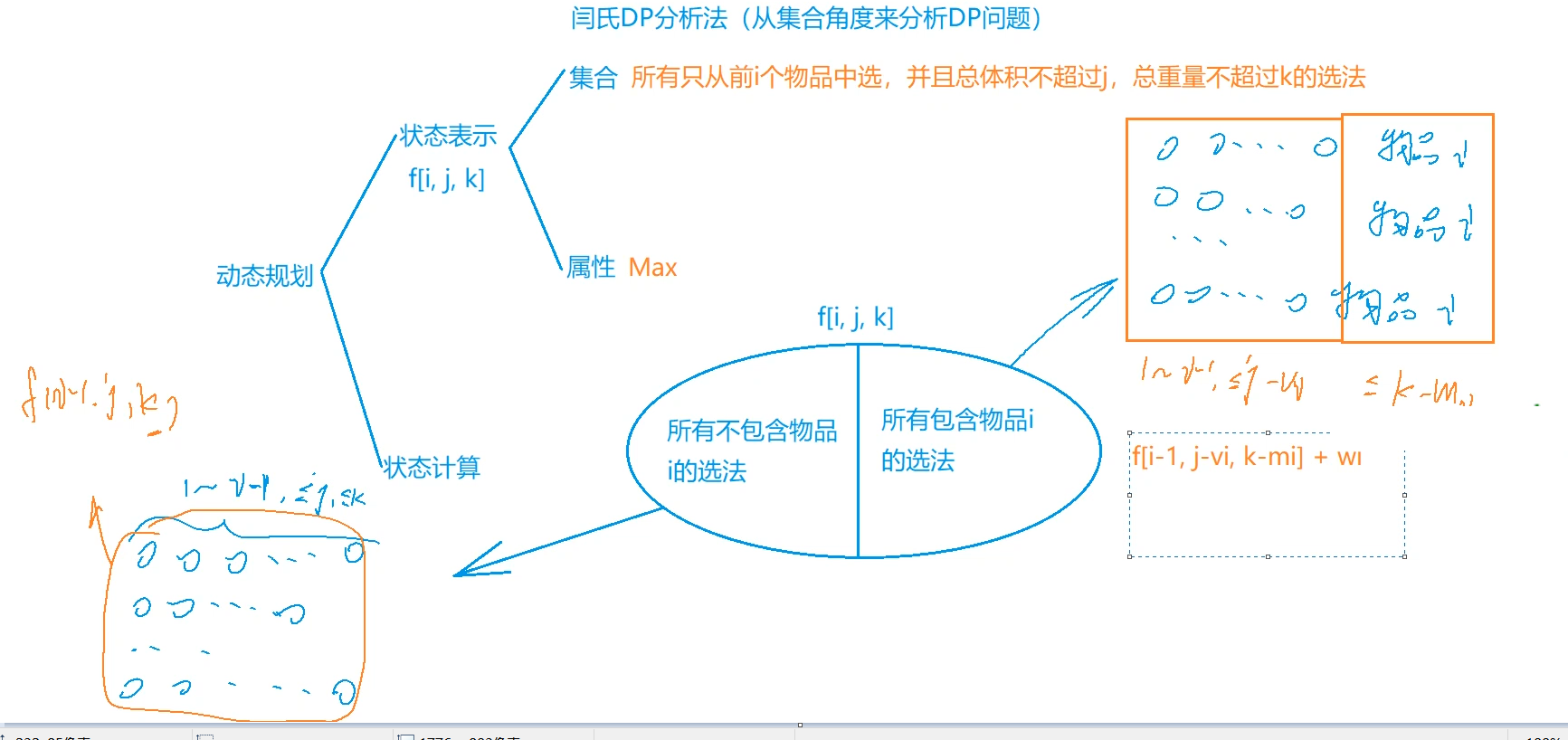
Knapsack problem with two-dimensional cost
Knapsack problem with two-dimensional cost
Problem solving analysis:
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010 ;
int n,m,V;
int f[N][N];
int main(){
cin>>n>>m>>V;
for(int i = 1 ; i <= n ; ++i){
int w1 , w2 ,v;
cin>>w1>>w2>>v;
for(int j = m ; j >= w1 ; --j)
for(int k = V ; k >= w2 ; k--)
f[j][k] = max(f[j][k] ,f[j-w1][k-w2] + v);
}
cout<<f[m][V]<<endl;
return 0;
}
diver
Problem solving ideas:
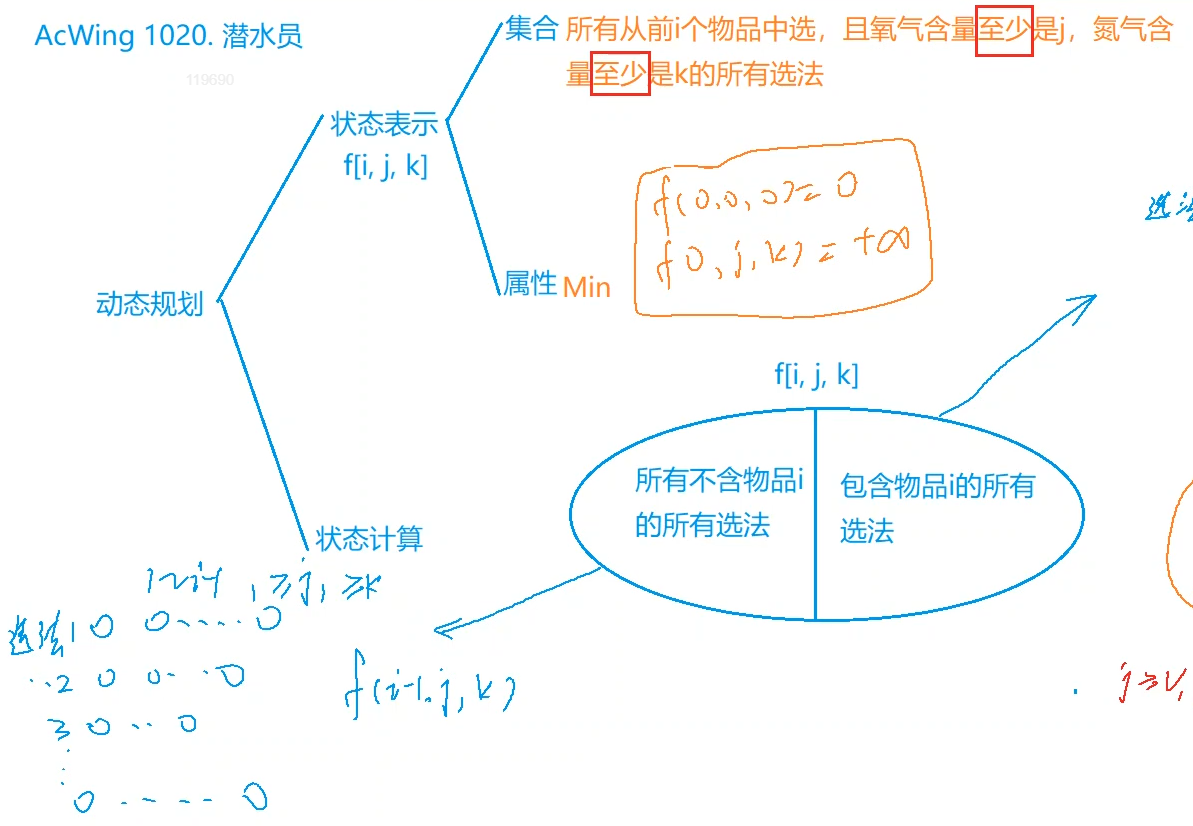
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 100;
int n,m , k;
int f[N][N];
int main(){
cin>>n>>m>>k;
memset(f , 0x3f , sizeof f);
f[0][0] = 0;
for(int i = 1 ; i <= k ; ++i){
int w1 ,w2 ,c;
cin>>w1>>w2>>c;
for(int j = n ; j >= 0 ; --j)
for(int k = m ; k >= 0 ; --k)
f[j][k] = min(f[j][k] ,f[max(0,j-w1)][max(0,k-w2)] + c);
}
cout<<f[n][m]<<endl;
return 0;
}
Grouping knapsack problem
Group Backpack
For grouped backpacks, each group of items can be selected or not. If selected, only one item in a group can be selected. So here we can know that the selection method within each group is similar to 01 backpack, so we have the following analysis
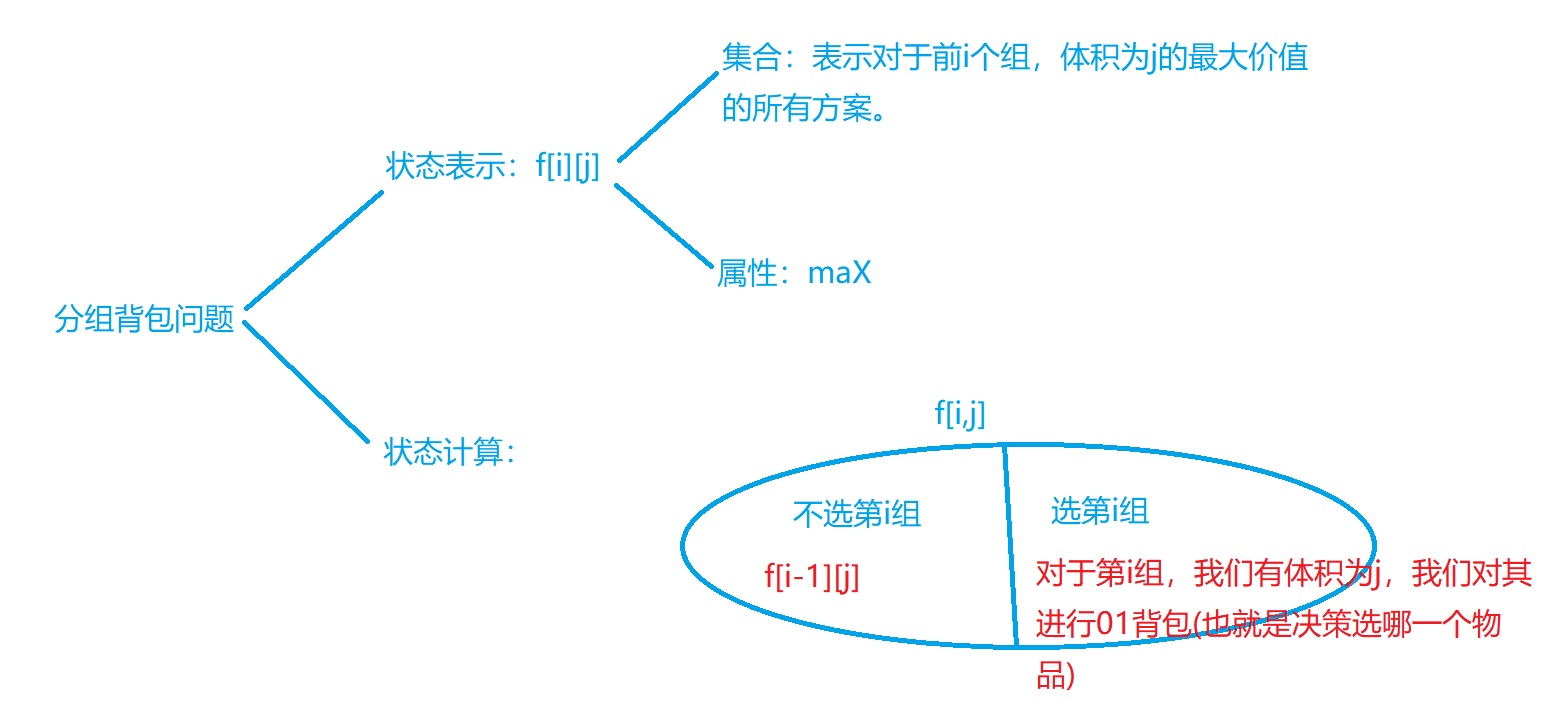
for(int i=1;i<=n;i++)
for(int j=0;j<=m;j++)
for(int k=1;k<=s[i];k++)//s[i] indicates the number of items in group I
if(j>=v[i][k])//The remaining Backpack Capacity j is greater than the volume of the k-th item in group i
{
f[i][j] = max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
}
Machine allocation (only one for each group)
Problem solving ideas:
Let's abstract the problem and regard the company as a group of items. The number of items in the company is m, the volume of each item is j, and the value is g[i][j]. For the scheme, we traverse each group in reverse order, and for each group, we find the corresponding quantity according to the dp calculation formula.
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 155;
int n ,m;
int f[N][N] , g[N][N];
int ans[N];
int main(){
cin>>n>>m;
for(int i = 1 ; i <= n ; ++i)
for(int j = 1; j <= m ; ++j)cin>>g[i][j];
for(int i = 1 ; i <= n ; ++i) // Number of groups
for(int j = 1; j <= m ; ++j) // volume
for(int k = 0 ; k <= j ; ++k) // Decision making, which can start from 0, means that none is selected
f[i][j] = max(f[i][j] ,f[i-1][j- k] + g[i][k]);
cout<<f[n][m]<<endl;
int res = f[n][m] , s = m ; // s is the total remaining volume
for(int i = n ; i >= 1 ; --i)
for(int k = 0 ; k <= s ; ++k)
if(res == f[i-1][s-k] + g[i][k]){
ans[i] = k;
s -= k; //Volume reduction
res -= g[i][k]; // Value reduction
break;
}
for(int i = 1 ; i <= n ;++i)cout<<i<<" "<<ans[i]<<endl;
return 0;
}
Jinming's budget plan (multiple in each group)
Problem solving ideas:
For the case of selecting more than one in each group, we can enumerate each possibility with binary. At the same time, one of the difficulties of this question is how to divide into groups. We can use vector to solve the problem (see the code for details)
code:
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
#define w first
#define v second
using namespace std;
typedef pair<int, int> PII;
const int N = 60, M = 32010;
int n, m;
PII master[N];
vector<PII> sv[N];
int f[M];
int main(){
cin>>m>>n;
for(int i = 1 ; i <= n ; ++i){
int w , v ,q;
cin>>w>>v>>q;
if(!q)master[i] = {w , w*v};
else sv[q].push_back({w,w*v});
}
for(int i = 1 ; i <= n ; ++i){
if(master[i].first)
for(int j = m ; j >= 0 ; --j){
int len = sv[i].size();
for(int k = 0 ; k < 1 << len;++k){
int w = master[i].first , v = master[i].second;
for(int u = 0; u < len;++u)
if( k >> u & 1) w += sv[i][u].w , v += sv[i][u].v;
if(j >= w)f[j] = max(f[j] , f[j-w] + v);
}
}
}
cout<<f[m]<<endl;
return 0;
}
Number of knapsack solutions
The number of schemes we calculated before only considers the volume, which represents the number of schemes filled with backpacks. This problem is to find the number of schemes of the optimal solution (maximum value).
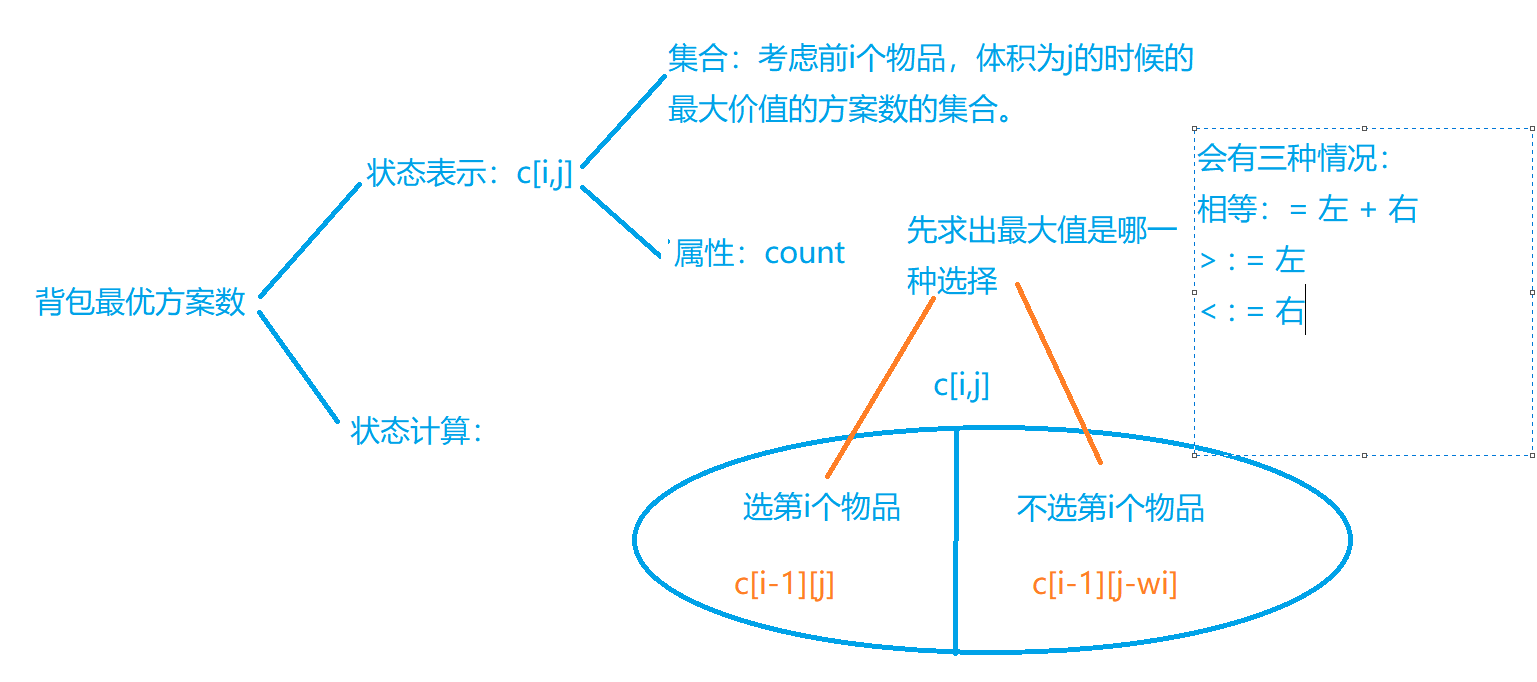
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010 , mod = 1e9 + 7;
int n , m;
int f[N] ,c[N];
int main(){
cin>>n>>m;
c[0] = 1;
for(int i = 1; i <= n ; ++i)
{
int w , v;
cin>>w>>v;
for(int j = m ; j >= w ; --j){
if(f[j] == f[j-w] + v)
c[j] = (c[j] + c[j-w] )%mod;
else if(f[j-w] + v > f[j] ) c[j] = c[j-w];
f[j] = max(f[j] , f[j-w] + v);
}
}
int cnt = 0;
for(int i = 0 ; i <= m ;++i)
if(f[i] == f[m])
cnt = (cnt + c[i])%mod;
cout<<cnt<<endl;
return 0;
}
Knapsack solution specific scheme
Problem solving ideas:
Generally speaking, one way to find a solution is to push back and record it in dp. Here we push back according to the formula of 01 knapsack.

code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010;
int n , m ;
int w[N] , v[N];
int f[N][N] , way[N];
int main(){
cin>>n>>m;
for(int i = 1 ; i <= n ; ++i)cin>>w[i]>>v[i];
for(int i = 1 ; i <= n ; ++i)
for(int j = 0 ; j <= m ; ++j){
f[i][j] = f[i-1][j];
if(j >= w[i])
f[i][j] = max(f[i-1][j] , f[i-1][j-w[i]] + v[i]);
}
int maxv = f[n][m] , s = m;
for(int i = n ; i ; --i)
if(f[i-1][s-w[i]] + v[i]== maxv)
way[i] = 1 , maxv -= v[i] , s -= w[i];
for(int i = 1 ; i <= n ; ++i)
if(way[i])cout<<i<<" ";
return 0;
}
Then some data is stuck and it is found that the title requires the smallest dictionary order, which is disgusting. Generally, we solve the problem of minimum dictionary order through greed. For this question, ask each item from front to back,
If we traverse from front to back according to the usual knapsack problem, we need to push back from back to front, which is not in line with the principle of greed. So we piled upside down at dp.
d
p
[
i
]
[
j
]
dp[i][j]
The volume of article j [i] [DP] does not exceed the maximum value.
code:
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1010;
int n , m ;
int w[N] , v[N];
int f[N][N] , way[N];
int main(){
cin>>n>>m;
for(int i = 1 ; i <= n ; ++i)cin>>w[i]>>v[i];
for(int i = n ; i >= 1 ; --i)
for(int j = 0 ; j <= m ; ++j){
f[i][j] = f[i+1][j];
if(j >= w[i])
f[i][j] = max(f[i][j] , f[i+1][j-w[i]] + v[i]);
}
int j = m;
for(int i = 1 ; i <= n ; ++i)
if(j >= w[i] && f[i][j] == f[i+1][j-w[i]] + v[i])
way[i] = 1 , j -= w[i];
for(int i = 1 ; i <= n ; ++i)
if(way[i])cout<<i<<" ";
return 0;
}