​

1.k-nearest neighbor algorithm

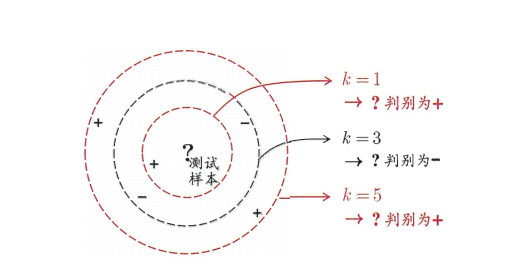
K-Nearest Neighbor learning (KNN) learning is a commonly used supervised learning method. Its working mechanism is very simple: given a test sample, find the K samples closest to it in the training set based on a certain distance measurement, and then predict through the k neighbor samples. If there are many neighbors in that category, the test sample is considered to be of that category. It is similar to "voting". The following figure is a real column of a KNN binary classification problem. It can be seen that the classification of test samples will be different according to the value of K, but they are all based on the voting of his neighbors.

The steps of KNN algorithm are given below:

① Calculate the distance between the unknown sample and the real column of all known samples.

② Sort distances from small to large

③ Select the nearest k known real columns

④ These k real neighbors vote. If the number of votes in which category is more, k is considered to be the member of that category

The calculated distance is generally Euclidean distance (Euclidean distance):

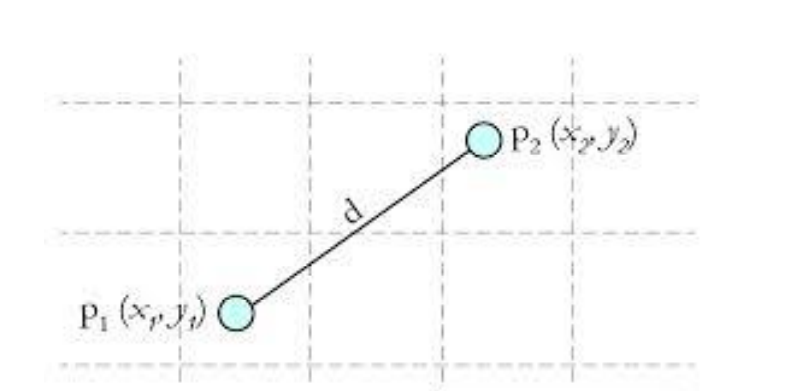
The Euclidean distance shown in the figure is:.
The disadvantages of the algorithm are: ① the complexity of the algorithm is high, and the distance between all known samples and samples to be classified needs to be calculated.

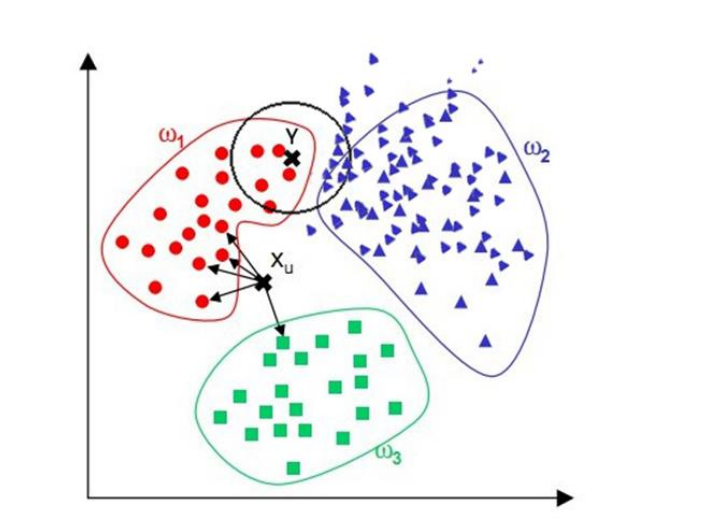
② When the sample distribution is unbalanced, for example, when one type of sample is too large (too many real columns) and dominated, the new unknown real column is easy to be classified as the dominant sample. It should be that the number of real columns of this type of sample is too large, but the new unknown real column is not actually close to the target sample. As for the black unknown sample points shown in the figure below, because the purple sample distribution is more dense than the red sample distribution, it is easy to divide the unknown sample into purple categories during classification, and it is obviously reasonable to divide it into red categories through observation.

2. Implementation of KNN algorithm

import matplotlib.pyplot as plt
import numpy as np
import operator

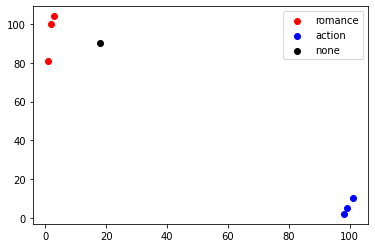
# Known classified data
x1 = np.array([3,2,1])
y1 = np.array([104,100,81])
x2 = np.array([101,99,98])
y2 = np.array([10,5,2])
scatter1=plt.scatter(x1,y1,c='r')
scatter2=plt.scatter(x2,y2,c='b')
# Unknown data
x = np.array([18])
y = np.array([90])
scatter3 = plt.scatter(x,y,c='k')
plt.legend(handles=[scatter1,scatter2,scatter3],labels=['romance','action','none'],loc='best')
plt.show()

​

​

x_data=np.array([[3,104],
                   [2,100],
                   [1,81],
                   [101,10],
                   [99,5],
                   [81,2]])
y_data=np.array(['A','A','A','B','B','B'])
x_test=np.array([18,90])

np.tile(x_test,(x_data.shape[0],1))#Assignment test

array([[18, 90],
       [18, 90],
       [18, 90],
       [18, 90],
       [18, 90],
       [18, 90]])

#Calculate x_data and x_test distance
distance=(((np.tile(x_test,(x_data.shape[0],1))-x_data)**2).sum(axis=1))**0.5
print(distance)

[ 20.51828453  18.86796226  19.23538406 115.27792503 117.41379817
 108.2266141 ]

#Sort from small to large
sotrdistance=distance.argsort()
sotrdistance

array([1, 2, 0, 5, 3, 4], dtype=int64)

classCount = {}
#Set k=5
k=5
for i in range(k):
    label=y_data[sotrdistance[i]]#Get label
    classCount[label]=classCount.get(label,0)+1#Count the number of tags

classCount

{'A': 3, 'B': 2}

# According to the operator Itemsetter (1) - the first value sorts classCount, and then reverses it
sotrclassCount=sorted(classCount.items(),key=operator.itemgetter(1), reverse=True)
sotrclassCount

[('A', 3), ('B', 2)]

#Get the largest number of tags
knn=sotrclassCount[0][0]
knn#So x_test should belong to category A

'A'

sorted(iterable, cmp=None, key=None, reverse=False)
Iteratable – iteratable object.
cmp - the function of comparison. This function has two parameters. The values of the parameters are taken from the iteratable object. The rules that this function must follow are: if it is greater than, it returns 1, if it is less than, it returns - 1, and if it is equal to, it returns 0.
key – it is mainly used to compare elements. There is only one parameter. The parameters of the specific function are taken from the iteratable object. Specify an element in the iteratable object to sort.
Reverse – collation, reverse = True descending, reverse = False ascending (default).

#operator. Itemsetter function
#The itemsetter function provided by the operator module is used to obtain the data of which dimensions of the object, and the parameters are some sequence numbers.
a = [('john', 'A', 15), ('jane', 'B', 12), ('dave', 'B', 10)]
b=operator.itemgetter(1)
b(a)

('jane', 'B', 12)

3. Realizing iris classification by KNN

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import random
from sklearn.metrics import classification_report 
from sklearn.model_selection import train_test_split
import operator

#knn
def knn(x_test,x_train,y_train,k):
    #Calculate x_test to X_ Euclidean distance of each point in the train
    distance=(((np.tile(x_test,(x_train.shape[0],1))-x_train)**2).sum(axis=1))**0.5
    sortdistance=distance.argsort()
    classCount={}
    for i in range(k):
        label=y_train[sortdistance[i]]
        classCount[label]=classCount.get(label,0)+1
        #Count the number of labels
    sortClassCount=sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    #Sort the values of the label dictionary keys
    #Get the largest number of tags
    return sortClassCount[0][0]

iris=datasets.load_iris()
x_train,x_test,y_train,y_test=train_test_split(iris.data,iris.target,test_size=0.2)
#Split dataset

print(x_test.shape,x_train.shape)
predictions=[]
for i in range(x_test.shape[0]):#For each x_test application knn
    predictions.append(knn(x_test[i],x_train,y_train,6))
print(classification_report(y_test,predictions))

(30, 4) (120, 4)
              precision    recall  f1-score   support

           0       1.00      1.00      1.00        11
           1       1.00      0.92      0.96        12
           2       0.88      1.00      0.93         7

    accuracy                           0.97        30
   macro avg       0.96      0.97      0.96        30
weighted avg       0.97      0.97      0.97        30

​

#Implemented with sklearn
from sklearn.neighbors import KNeighborsClassifier
model=KNeighborsClassifier(n_neighbors=6)
model.fit(x_train,y_train)
prediction1=model.predict(x_test)
print(classification_report(y_test,prediction1))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        11
           1       1.00      0.92      0.96        12
           2       0.88      1.00      0.93         7

    accuracy                           0.97        30
   macro avg       0.96      0.97      0.96        30
weighted avg       0.97      0.97      0.97        30

​

​