kruskal algorithm (kruskal algorithm) detailed explanation
There are two common methods to find the minimum spanning tree in connected networks, which are called prim algorithm and Kruskal algorithm. In this section, we will explain the Kruskal algorithm to you.
The method of Kruskal algorithm to find the minimum spanning tree is to sort all edges in the connected network in ascending order according to the weight size, and select from the edge with the smallest weight. As long as this edge does not form a loop with the selected edge, it can be selected to form the minimum spanning tree. For a connected network with N vertices, N-1 qualified edges are selected, and the spanning tree composed of these edges is the minimum spanning tree.
For example, figure 1 is a connected network. The cruzcar algorithm needs to go through the following steps to find the minimum spanning tree corresponding to figure 1:
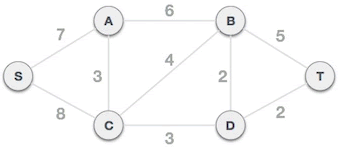
Figure 1 connected network
- Sort all edges in the connected network in ascending order according to the weight:

- Start from the B-D edge. Since no edge has been selected to form the minimum spanning tree, and B-D itself will not form a loop, the B-D edge can form the minimum spanning tree.
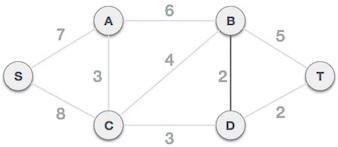
Fig. 2 minimum spanning tree composed of B-D edges
- The D-T edge will not form a loop with the selected B-D edge, and can form a minimum spanning tree:
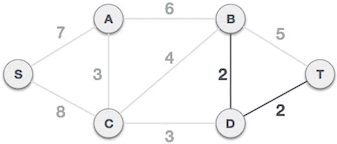
Fig. 3 minimum spanning tree composed of D-T edges
- A-C edges will not form a loop with the selected B-D and D-T edges, and can form a minimum spanning tree:
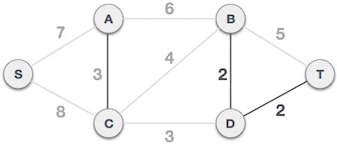
Fig. 4 minimum spanning tree composed of a-C edges
- The C-D edge will not form a loop with the selected A-C, B-D and D-T edges, and can form a minimum spanning tree:
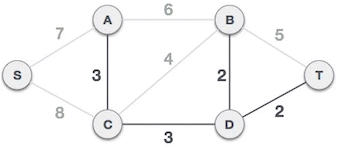
Fig. 5 minimum spanning tree composed of C-D edges
- The C-B edge will form a loop with the selected C-D and B-D edges, so it cannot form a minimum spanning tree:
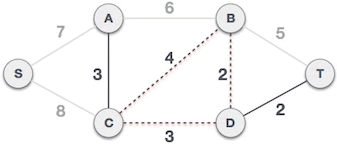
Fig. 6 C-B edges cannot form a minimum spanning tree
- B-T, A-B and S-A will form a loop with the selected A-C, C-D, B-D and D-T, and cannot form a minimum spanning tree. S-A does not form a loop with the selected edges, and can form a minimum spanning tree.
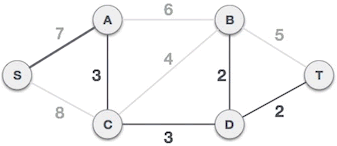
Fig. 7 minimum spanning tree composed of S-A edges
- As shown in Figure 7, for a connected network with 6 vertices, we have selected 5 edges, and the spanning tree composed of these edges is the minimum spanning tree.
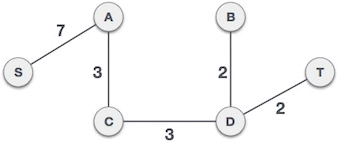
Fig. 8 minimum spanning tree
Implementation of Kruskal algorithm
The difficulty of realizing Kruskal algorithm is "how to judge whether a new edge will form a loop with the selected edge". Here is a judgment method: in the initial state, configure different markers for each vertex in the connected network. For a new edge, if the marks of the vertices at both ends are different, it will not form a loop and can form a minimum spanning tree. Once the new edge is selected, its two vertices and the vertices at both ends of all the selected edges directly connected to it need to be changed to the same mark; Conversely, if the marks of the vertices at both ends of the new edge are the same, it means that a loop will be formed.
For example, in Figure 4 above, the selected edges are A-c, B-D and d-t. next, it is necessary to judge whether the C-D edges can form A minimum spanning tree. For the selected edge, B-D and D-T are directly adjacent, so the marks of B, D and T are the same (assumed to be 1), and the marks of vertices at both ends of A-C edge are the same (assumed to be 2). Judge whether the C-D edge can form A minimum spanning tree. Because the marks of C and D are different (1 ≠ 2), it can form A minimum spanning tree. C-D is the newly selected edge, and the selected edges connected to it include A-c, B-D and d-t. therefore, A, C, D, B and t should be changed to the same mark.
For another example, judge whether C-B can form a minimum spanning tree based on Fig. 5. According to the analysis results of the above example, the marks of C and B vertices are the same, so the C-B edge will form a loop with other selected edges and cannot form a minimum spanning tree (as shown in Fig. 6).
The following is a C language program for finding the minimum spanning tree in the connected network shown in Figure 1 with Kruskal algorithm:
#include <stdio.h>
#include <stdlib.h>
#define N 9 / / number of edges in the graph
#define P 6 / / number of vertices in the graph
//Construct a structure that represents edges
struct edge {
//An edge has 2 vertices
int initial;
int end;
//Weight of edge
int weight;
};
//Used in the qsort sorting function to sort the edges in the edges structure in ascending order according to the weight
int cmp(const void* a, const void* b) {
return ((struct edge*)a)->weight - ((struct edge*)b)->weight;
}
//Kruskal algorithm finds the minimum spanning tree, edges stores the edges of the graph entered by the user, and minTree is used to record the edges of the minimum spanning tree
void kruskal_MinTree(struct edge edges[], struct edge minTree[]) {
int i, initial, end, elem, k;
//Each vertex is configured with a tag value
int assists[P];
int num = 0;
//In the initial state, the marking of each vertex is different
for (i = 0; i < P; i++) {
assists[i] = i;
}
//Sort all edges in ascending order according to the weight
qsort(edges, N, sizeof(edges[0]), cmp);
//Traverse all edges
for (i = 0; i < N; i++) {
//Find the position subscript of the two vertices of the current edge in the assists array
initial = edges[i].initial - 1;
end = edges[i].end - 1;
//If the vertex position exists and the vertex marks are different, it means that it is not in a set and no circuit will be generated
if (assists[initial] != assists[end]) {
//Record the edge as part of the minimum spanning tree
minTree[num] = edges[i];
//Count + 1
num++;
elem = assists[end];
//Change all the vertex marks newly added to the spanning tree to the same
for (k = 0; k < P; k++) {
if (assists[k] == elem) {
assists[k] = assists[initial];
}
}
//If the difference between the number of selected edges and the number of vertices is 1, it proves that the minimum spanning tree has been formed and exits the loop
if (num == P - 1) {
break;
}
}
}
}
void display(struct edge minTree[]) {
int cost = 0, i;
printf("The minimum spanning tree is:\n");
for (i = 0; i < P - 1; i++) {
printf("%d-%d Weight:%d\n", minTree[i].initial, minTree[i].end, minTree[i].weight);
cost += minTree[i].weight;
}
printf("The total weight is:%d", cost);
}
int main() {
int i;
struct edge edges[N], minTree[P - 1];
for (i = 0; i < N; i++) {
scanf("%d %d %d", &edges[i].initial, &edges[i].end, &edges[i].weight);
}
kruskal_MinTree(edges, minTree);
display(minTree);
return 0;
}
Java program for finding the minimum spanning tree in the connected network shown in Figure 1 using Kruskal algorithm:
import java.util.Arrays;
import java.util.Scanner;
public class prim {
static int N = 9; // Number of edges in the graph
static int P = 6; // Number of vertices in the graph
//Build a class that represents a path
public static class edge implements Comparable<edge>{
//Each path has 2 vertices and 1 weight
int initial;
int end;
int weight;
public edge(int initial, int end, int weight) {
this.initial = initial;
this.end = end;
this.weight = weight;
}
//Sort each edge object in ascending order according to its weight
@Override
public int compareTo(edge o) {
return this.weight - o.weight;
}
}
public static void kruskal_MinTree(edge[] edges,edge [] minTree) {
int []assists = new int[P];
//Each vertex is configured with a different tag value
for (int i = 0; i < P; i++) {
assists[i] = i;
}
//Sort all edges in ascending order according to the weight
Arrays.sort(edges);
//Traverse all edges
int num = 0;
for (int i = 0; i < N; i++) {
//Find the position subscript of the two vertices of the current edge in the assists array
int initial = edges[i].initial - 1;
int end = edges[i].end - 1;
//If the vertex position exists and the vertex marks are different, it means that it is not in a set and no circuit will be generated
if (assists[initial] != assists[end]) {
//Record the edge as part of the minimum spanning tree
minTree[num] = edges[i];
//Count + 1
num++;
int elem = assists[end];
//Do not change the vertex markers newly added to the spanning tree to the same
for (int k = 0; k < P; k++) {
if (assists[k] == elem) {
assists[k] = assists[initial];
}
}
//If the difference between the number of selected edges and the number of vertices is 1, it proves that the minimum spanning tree has been formed and exits the loop
if (num == P - 1) {
break;
}
}
}
}
public static void display(edge [] minTree) {
System.out.println("The minimum spanning tree is:");
int cost = 0;
for (int i = 0; i < P - 1; i++) {
System.out.println(minTree[i].initial+" - "+ minTree[i].end+" The weight is:"+minTree[i].weight);
cost += minTree[i].weight;
}
System.out.print("The total weight is:"+cost);
}
public static void main(String[] args) {
Scanner scn = new Scanner(System.in);
edge[] edges = new edge[N];
edge[] minTree = new edge[P-1];
System.out.println("Please enter the information of each edge in the figure:");
for(int i=0;i<N;i++) {
int initial = scn.nextInt(), end = scn.nextInt(), weight = scn.nextInt();
edges[i] = new edge(initial,end,weight);
}
kruskal_MinTree(edges,minTree);
display(minTree);
}
}
Python program for finding the minimum spanning tree in the connected network shown in Figure 1 using Kruskal algorithm:
N = 9 #Number of edges in the graph
P = 6 #Number of vertices in the graph
#Construct a structure that represents edges
class edge:
#An edge has 2 vertices
initial = 0
end = 0
#Weight of edge
weight = 0
def __init__(self,initial,end,weight):
self.initial = initial
self.end = end
self.weight = weight
edges = [] # It is used to save the information of each edge of the graph entered by the user
minTree=[] # Save the information of each edge of the minimum generation number
#Enter information for N edges
for i in range(N):
li = input().split()
initial = int(li[0])
end = int(li[1])
weight = int(li[2])
edges.append(edge(initial,end,weight))
# Sort the edges list according to weight
def cmp(elem):
return elem.weight
#Kruskal algorithm for finding minimum spanning tree
def kruskal_MinTree():
#Record the number of selected edges
num = 0
#Configure a different tag for each vertex
assists = [i for i in range(P)]
#Sort the edges list
edges.sort(key = cmp)
#Traverse N edges and reselect the edges that can form the minimum spanning tree
for i in range(N):
#Find the position subscript of the two vertices of the current edge in the assists array
initial = edges[i].initial -1
end = edges[i].end-1
# If the vertex position exists and the vertex marks are different, it means that it is not in a set and no circuit will be generated
if assists[initial] != assists[end]:
# Record the edge as part of the minimum spanning tree
minTree.append(edges[i])
#Count + 1
num = num+1
#Change all the vertex marks newly added to the spanning tree to the same
elem = assists[end]
for k in range(P):
if assists[k] == elem:
assists[k]= assists[initial]
#If the difference between the number of selected edges and the number of vertices is 1, it proves that the minimum spanning tree has been formed and exits the loop
if num == P-1:
break
def display():
cost = 0
print("The minimum spanning tree is:")
for i in range(P-1):
print("%d-%d Weight:%d"%(minTree[i].initial, minTree[i].end, minTree[i].weight))
cost = cost + minTree[i].weight
print("The total weight is:%d"%(cost))
kruskal_MinTree()
display()
The vertices A, B, C, D, S and T in Figure 1 are represented by numbers 1 ~ 6 respectively. The execution results of the above procedures are as follows:
5 1 7
5 3 8
1 2 6
1 3 3
3 2 4
3 4 3
2 4 2
2 6 5
4 6 2
The minimum spanning tree is:
2-4 weight: 2
4-6 weight: 2
1-3 weight: 3
3-4 weight: 3
5-1 weight: 7
Total weight: 17