Title:
Everyone must have played the "fruit ninja" game popular all over the world in 2010? (it doesn't matter if you haven't played ~) in the game, a series of fruits and bombs will be ejected randomly in the screen. Players can complete the tasks specified in the game by cutting off all fruits as much as possible to avoid hitting the bomb. If the player can cut down a series of fruits in the picture with one knife, there will be additional rewards, as shown in Figure 1.

Figure 1
Now, if you are a player of the "fruit ninja" game, one thing you have to do is cut off the fruit in the picture. The problem seems a little complicated. Let's simplify it. We imagine the game world as a two-dimensional plane. Each fruit in the game is simplified into a vertical line segment perpendicular to the horizontal line. We only consider whether we can find a straight line so that it can pass through all the segments representing fruit.
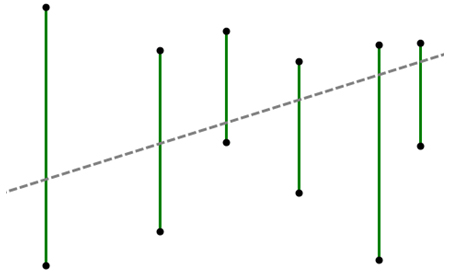
Figure 2
As shown in Figure 2, the green vertical line segment represents one fruit by one; The gray dotted line represents a line passing through all segments. As can be seen from the above figure, for the arrangement of such a group of line segments, we can find a scheme to cut all fruits with one knife.
In addition, we agree that if a line just passes through the endpoint of the line segment, it also means that it has cut the fruit represented by the line segment. If you are the developer of such a function, how do you find a straight line through them?
Input format:
Input gives a positive integer on the first line
N
(
≤
1
0
4
)
N(≤10^4)
N (≤ 104), indicating the number of fruits. Then n lines, each giving three integers
x
,
y
1
,
y
2
x,y_1,y_2
x. y1 and y2 are separated by spaces, indicating that one end point is
(
x
,
y
1
)
(x,y_1)
(x,y1) and
(
x
,
y
2
)
(x,y_2)
(x,y2), where
y
1
>
y
2
y_1>y_2
y1>y2. Note: the given fruit input set must have a straight line that can pass through it all, regardless of the non existence. Coordinate is interval
[
−
1
0
6
,
1
0
6
)
[−10^6 ,10^6 )
An integer in [− 106106).
Output format:
Output any two points with integer coordinates on the line passing through all segments in one line p 1 ( x 1 , y 1 ) p_1(x_1,y_1) p1 (x1, y1) and p 2 ( x 2 , y 2 ) p_2(x_2,y_2 ) p2 (x2, y2) in the format x 1 y 1 x 2 y 2 x_1 y_1 x_2 y_2 x1y1x2y2. Note: the answer to this question is not unique. It is determined by the special referee procedure, but there must be a solution in which the four coordinates are all integers.
Input example:
5 -30 -52 -84 38 22 -49 -99 -22 -99 48 59 -18 -36 -50 -72
Output example:
-99 -99 -30 -52
Idea:
Find the range of slope with the lowest endpoint of each line segment. If a slope can cut off all line segments, output and return.
code:
#include<bits/stdc++.h>
using namespace std;
//Use double to calculate the slope easily
struct node{
double x;
double maxy;
double miny;
}s[10005];
//All segments are arranged from left to right
bool cmp(node a,node b){
return a.x<=b.x;
}
const double inf=999999999;
int ansid;
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>s[i].x>>s[i].maxy>>s[i].miny;
}
sort(s+1,s+1+n,cmp);
for(int i=1;i<=n;i++){
// Maximum and minimum slope
double ansmaxk=inf;
double ansmink=-inf;
double maxk,mink;
int j;
for(j=1;j<=n;j++){
if(i==j){
continue;
}
// j is on the left of i
if(j>i){
maxk=(s[j].maxy-s[i].miny)/(s[j].x-s[i].x);
mink=(s[j].miny-s[i].miny)/(s[j].x-s[i].x);
}
// j is on the right of i
else{
maxk=(s[i].miny-s[j].miny)/(s[i].x-s[j].x);
mink=(s[i].miny-s[j].maxy)/(s[i].x-s[j].x);
}
// Out of range
if(mink>ansmaxk||maxk<ansmink){
break;
}
// Update the slope and use the maximum convenient output
if(maxk<ansmaxk){
ansmaxk=maxk;
// Record the answer on that line segment
ansid=j;
}
ansmink=max(mink,ansmink);
}
// All segments are in range
if(j==n+1){
printf("%.0lf %.0lf %.0lf %.0lf",s[i].x,s[i].miny,s[ansid].x,s[ansid].maxy);
return 0;
}
}
return 0;
}