Large top pile and small top pile

What is a heap

The essence of heap is a one-dimensional array maintained by the structure of complete binary tree.
According to the characteristics of the reactor, the reactor is divided into large top reactor and small top reactor
Large top heap: the value of each node is greater than or equal to the value of the left and right child nodes
Small top heap: the value of each node is less than or equal to the value of the left and right child nodes

Why heap

When we maintain the priority queue, if we use the ordinary sorting method, the time complexity is too high. We use heap to maintain an orderly structure that is updated at any time.
What we need is the minimum or maximum value in the heap. Through the heap structure, the time complexity of inserting or extracting values is low enough. Because it is divided into arbitrary subsets, and then subsets are divided continuously, its search and insertion efficiency is high.

Characteristics of reactor

Memory occupation: ordinary trees occupy a large memory space, because we must allocate memory for nodes and left and right pointers. However, the heap is saved in an array, so the memory occupation of the heap structure is small.
Time complexity: the time complexity in the heap can reach On*log(2n).
Search speed: the search speed of the heap is very slow, because the purpose of the heap is to put the largest (smallest) node in front, so as to quickly insert and delete

Large top heap sorting process

1. Give an array

let a = [7,3,8,5,1,2]

2. Construct binary tree

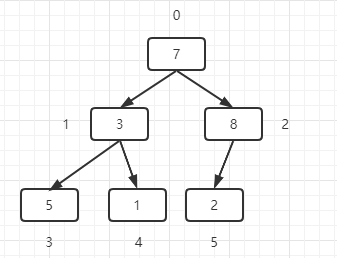
Now we need to turn this sequence into our heap.

• Ascending order: large top reactor
  +The value of each node is greater than that of the left and right child nodes. The value of the root node is the largest. Then exchange the position between the root node and the last node, and the end is the largest element.
• Descending order: small top reactor

Process of constructing large top pile

• 1. Find the last non leaf node. The index of the last non leaf node is: arr.length/2 + 1, that is, 6 / 2 + 1 = 2. Then compare the value of the node with its child nodes. If the node is smaller than the child tree, exchange it.
  

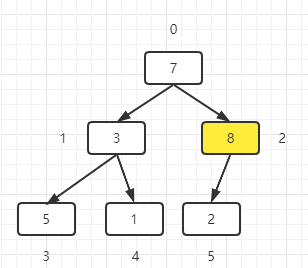
• 2. Find the next non leaf node, which is actually the current coordinate - 1. Here is node 1. Ensure that the value of node 1 is greater than that of the child node.
  

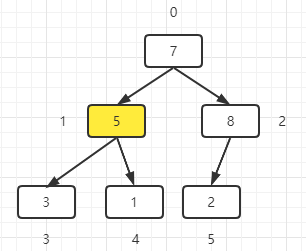
• 3. Find the next non leaf node and ensure that the value of this node is greater than that of the child node
  

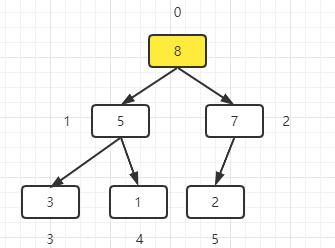
Constructing priority queue through large top heap

• How to get the parent node index of each node: ~ ~ ((index-1) / 2)
• Bitwise operator ~ ~: you can use a bitwise operator to replace the math of a positive number Floor(), replacing math. For negative numbers ceil( ). The advantage of the double no positioning operator is that it performs the same operation faster.

// First, define a class that requires methods for joining and leaving the queue
class PriorityQueue{
	// When new, arr can be passed in
    constructor(arr){
        if (arr.length){
            // Constructing a heap from an array
            this.tree = []
            this._build_tree(arr);
            return;
        }
        this.tree = [];
    }

    // Join the team
    enqueue(val){
        // Put the value in the last bit of the array tree
        // Put the value directly on the leaf node, and then perform the floating operation
        this.tree.push(val);
        // this.tree.length-1 is the index of the value put in
        this._up(this.tree.length - 1);
    }

    // Out of the team
    dequeue(){
        // Take tree root element
        this.tree.shift();
        // Put the last element in the root position and sink
        let last = this.tree.pop();
        this.tree.unshift(last);
        // log(n) sink
        this._down(0);
    }

    // Take the value of team leader
    getFirst(){
        return this.tree[0];
    }

    _build_tree(arr){
        let tree = this.tree;
        tree.push(arr[0]);
        for (let i = 1; i < arr.length; i++){
            // Put the element in the root position
            tree.unshift(arr[i]);
            // Sink element 0
            this._down(0);
        }
    }
}

Implementation of sinking code

• 1. First, you need to get the last node that is not a leaf node
• 2. Maintain the value of the node so that the value of the node is greater than that of the child node

    _down(index){
        let tree = this.tree;
        // Gets the index of the last node that is not a leaf node
        let last_no_leaf = ~~((tree.length - 2) / 2);
        // index is the leaf node, which is already at the bottom. There is no need to sink
        if (index > last_no_leaf) return;
        // If index is not a leaf node
        while(index <= last_no_leaf){
            let l = tree[index * 2 + 1];
            let r = tree[index * 2 + 2] || tree[index * 2 + 1]; // There may be no right son
            // Get the maximum value in the left and right child nodes
            let max = l >= r ? l : r;
            let maxIndex = l >= r ? index * 2 + 1: index * 2 + 2
            if (tree[index] < max){
                // Exchange with maximum
                [tree[index], tree[maxIndex]] = [tree[maxIndex], tree[index]]
                // When the corresponding value reaches the MaxIndex position, continue to sink it
                index = maxIndex;
            }else{
                return;
            }
        }
    }

Implementation of floating code

    _up(index){
        let tree = this.tree;
        // This value does not reach the root node
        while(index !== 0){
            // Parent node found
            let p = ~~((index - 1) / 2);
            // If it is larger than the parent node, it will be swapped, and then continue to compare with the previous node
            if (tree[index] > tree[p]){
                [tree[index], tree[p]] = [tree[p], tree[index]];
                // let tmp = index;
                // this._down(tmp);
                index = p;
            } else {
                return;
            }
        }
    }