PID algorithm type

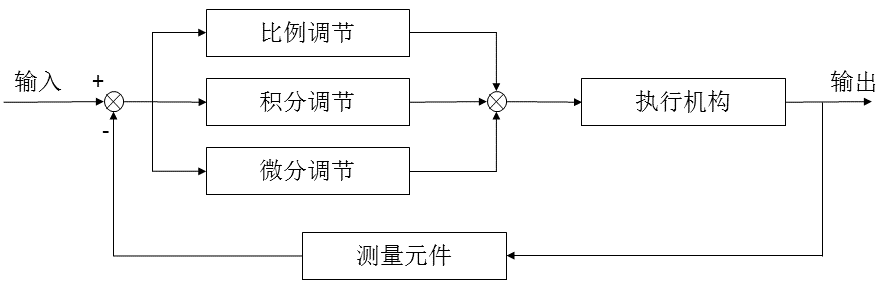
There are two forms of PID algorithm in engineering

First define a structure

typedef struct PID 
{
    float  Proportion;//P
	float  Integral;  //I
	float  Derivative;//D
    
	float  PrevError;//Last error
	float  LastError;//Last error
	float  Error;	 //Current error
    float  DError;
	float  SumError; //Cumulative sum of historical errors
    
	float  Integralmax;
	float  output;	   //output
	float  outputmax;
	float  errormax;
	u8 first_flag;
	float  deadzone;   //dead zone
}PID;

• Positional type

void PID_position_PID_calculation(PID *pp, float CurrentPoint, float NextPoint)  
{   
	if(pp->first_flag == 1)
	{
		pp->LastError = NextPoint - CurrentPoint;
		pp->PrevError = NextPoint - CurrentPoint;
		pp->first_flag = 0;
	}
	pp->Error =  NextPoint -  CurrentPoint;          
	pp->SumError += pp->Error;                      
	pp->DError = pp->Error - pp->LastError;
	
	pp->output =  pp->Proportion * pp->Error + PID_abs_limit(pp->Integral * pp->SumError, pp->Integralmax ) + pp->Derivative * pp->DError ;  

    //Output limiting
	if(pp->output > pp->outputmax )  pp->output = pp->outputmax;
	if(pp->output < - pp->outputmax )  pp->output = -pp->outputmax; 
	pp->LastError = pp->Error;
	
	if(float_abs(pp->Error) < pp->deadzone)
	{
		pp->output = 0;
	}
}

• Incremental

void PID_incremental_PID_calculation(PID *pp, float CurrentPoint, float NextPoint)  
{  
    //Error calculation
	pp->Error =  NextPoint - CurrentPoint;                               
	pp->DError = pp->Error - pp->LastError;
	
    //PID algorithm
	pp->output +=  pp->Proportion * (pp->DError)+ PID_abs_limit(pp->Integral * pp->Error, pp->Integralmax ) + pp->Derivative * ( pp->Error +  pp->PrevError - 2*pp->LastError);  

    //Output limiting
	if(pp->output > pp->outputmax )  pp->output = pp->outputmax;
	if(pp->output < - pp->outputmax )  pp->output = -pp->outputmax;
	pp->PrevError = pp->LastError;  
	pp->LastError = pp->Error;
	
    //dead zone
	if(float_abs(pp->Error) < pp->deadzone)
	{
		pp->output = 0;
	}
}

The difference between incremental and positional

• The incremental algorithm does not need to accumulate, and the determination of the increment of the control quantity is only related to the recent deviation sampling values, and the calculation error has little influence on the calculation of the control quantity;

  The positional algorithm uses the cumulative value of past deviation, which is easy to produce large cumulative error.

• The incremental algorithm obtains the increment of control quantity. For example, in valve control, only the change part of valve opening is output, and the impact of misoperation is small. If necessary, this output can be limited or prohibited through logical judgment, which will not seriously affect the work of the system;

  The output of position type directly corresponds to the output of the object, so it has a great impact on the system.

• The output of incremental PID control is the increment of control quantity, which has no integral effect. Therefore, this method is suitable for objects with integral parts of actuator, such as stepping motor, etc;

  The position PID is suitable for objects with actuator without integral parts, such as electro-hydraulic servo valve.

• In PID control, position PID needs integral limiting and output limiting;

  The incremental PID only needs to output amplitude limiting.

Advantages and disadvantages of position PID

• Advantages: position PID is a non recursive algorithm, which can directly control the actuator (such as the balance trolley). The value of u(k) corresponds to the actual position of the actuator (such as the current angle of the trolley), so it can be well used in the object without integral parts of the actuator.
• Disadvantages: each output is related to the past state, e(k) should be accumulated during calculation, and the calculation workload is large.

Advantages and disadvantages of incremental PID

• advantage:
  • The impact of misoperation is small, and the wrong data can be removed by logical judgment when necessary
  • The impact is small during manual / automatic switching, which is convenient for undisturbed switching. When the computer fails, it can still maintain the original value.
  • There is no need to accumulate in the formula. Control increment Δ The determination of u(k) is only related to the last three sampling values.
• Disadvantages:
  • Large integral truncation effect and steady-state error;
  • Spillover has a great impact, and some controlled objects are not good to use incremental.

sketch

The purpose of PID algorithm is to minimize the error and make the actual value reach the expected value as much as possible.
However, there are always errors in the system, so the actual value will be lower or higher than the expected value without PID control. At this time, if P-loop regulation is added, that is, the output value is related to the product of error and Kp, and is directly related to the size of error. Therefore, the output of the system is very large when it is just started, and gradually decreases when it is close to the expectation, but there is still output, resulting in overshoot. Therefore, the choice of Kp is very particular. If it is too large, the shock amplitude is too large, and if it is too small, the shock time is long.
If i-loop regulation is added, I is the accumulation of error. After the system overshoot, the error symbol changes to reduce the integral or even negative value. At this time, the output of the system is restrained and the output is reduced, so as to make the system stable quickly.
In D-loop regulation, D is the differential, which is the slope of error change, that is, the speed of change. Its function is to improve the response speed. It has no effect on the system with no change in error, and it is easy to overshoot the system with drastic change in error.
The conclusion is that P allows the error to be 0, I makes the error faster and smoother to be 0, and D makes the system respond faster.