Chapter X internal sorting

Linear table operation

Union of unordered linear tables:

For example: A = (17, 55, 9, 30, 28)

​ B = (30，68，5，17)

Time complexity O(LA*LB)

Union of ordered linear tables:

For example: A = (7, 15, 29, 38)

​ B = (3，7，46，57)

Time complexity O(LA+LB)

lookup

Sequential lookup of unordered tables: O(n)

Sequential lookup of ordered table: O(logn)

And the idea of sorting is involved in the process of Constructing Binary sorting tree and B tree.

Sorting overview

Basic concepts related to sorting:

Record / element: the basic unit of sorting

Sequence: all records to be sorted

Sort: rearrange any sequence of data elements (or records) into a sequence ordered by keywords.

Keyword: sort by primary keyword / secondary keyword / combination of several data items

Strict definition of sorting:

If the sequence to be sorted just meets the sorting requirements, it is called "positive sequence"

If the sequence to be sorted is reversed and just meets the sorting requirements, it is called "reverse order" sequence

Stability of sorting:

Suppose Ki = Kj and Ri is ahead of Rj in the sequence before sorting (i.e. I < J)

If Ri is still ahead of Rj in the sequence after sorting, the sorting method used is said to be stable.

On the contrary, if it is possible to make the sorted sequence Rj ahead of Ri, the sorting method used is said to be unstable.

Multi keyword sorting: records are sorted by multiple keywords. (except for the first sorting, the following sorting must use a stable sorting method)

Sort by:

Internal sorting: the sorting process in which the records to be sorted are stored in computer random access memory.

External sorting: the number of records to be sorted is so large that the memory cannot hold all records at one time. During the sorting process, it is still necessary to access the external memory.

Performance of internal sorting algorithm:

1. Time performance

   Original operation: keyword comparison and record movement

   The cost in three cases: the best case (minimum time cost), the worst case (maximum time cost) and the average case.

2. Auxiliary space

   Other storage space required in addition to the records to be sorted

3. Complexity of the algorithm itself

Classification of internal sorting:

According to different principles: insert sort, exchange sort, select sort, merge sort and cardinal sort.

According to the required workload:

1. Simple sorting method: O(n*n) bubble sorting simple selection sorting direct insertion sorting
2. Advanced sorting algorithm: O(nlogn) Hill sort heap sort merge sort quick sort
3. Cardinality sorting: O(d*n)

There are three ways to store sequences:

Record movement can be reduced or avoided by changing the storage mode of records

Storage method of the sequence to be sorted:

1. Stored in a group of storage units with continuous addresses, the order relationship between records is determined by the storage location, and the sorting must move elements.
2. In the static linked list, the order relationship between records is indicated by the pointer. Sorting does not need to move the records, but only needs to modify the pointer (linked list sorting).
3. The records to be sorted are stored in a group of storage units with continuous addresses, and an address vector indicating the storage location of the records is attached. The sorting process does not move the records, but moves the addresses of these records in the address vector. After sorting, the storage location of the records is adjusted according to the value in the address vector (address sorting).

Take the first storage method as an example:

#define MAXSIZE 20 		// The maximum length of a small sequential table used as an instance.
typedef int KeyType;	//Define keyword type as integer type
typedef struct{
	KeyType key;	//Keyword item
	InfoType otherinfo; //Other data items
}RedType;
typedef struct{
	RedType r[MAXSIZE+1]; //r[0] idle or used as sentry unit
	int length; //Sequence table length
}SqList; //Sequence table type

Insert sort

Basic idea of insertion sorting:

The sequence to be sorted is divided into two parts: the front is orderly and the rear is disordered.

Initial: the front contains only the first record, and the rear contains the remaining n-1 records.

Insert the first record of the rear species into the front ordered table according to the keyword size in each trip.

Final: the front contains all records and the rear is empty.

Different insertion sorting algorithms:

According to different search methods:

1. Direct insert sort
2. Binary Insertion Sort
3. Shell Sort

Reduce the number of moves:

1. 2-way insertion sort
2. Table insert sort

Direct insert sort

1. Initialization: the first record r[1] in the sequence is regarded as an ordered subsequence.

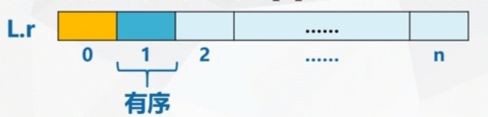
1. One pass insertion: use the direct search method to find the appropriate insertion position for the i(i=2,3,4... n) record r[i] in the ordered subsequence r[1... i-1] containing i-1 records, so as to obtain the ordered subsequence r[1... I] containing I records

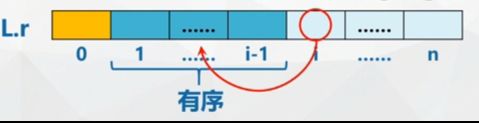
1. Repeat step 2 for n-1 times to turn the whole sequence into an ordered sequence.

void InsertSort(SqList &L){
	for(int i=2;i<=L.length;++i)
		if(L.r[i].key<L.r[i-1].key){
			L.r[0]=L.r[i];
			L.r[i]=L.r[i-1];
			for(int j=i-2;L.r[0].key<L.r[j].key;--j)
				L.r[j+1] = L.r[j];	//Move back
			L.r[j+1]=L.r[0];
		}
}

For example: (stable)

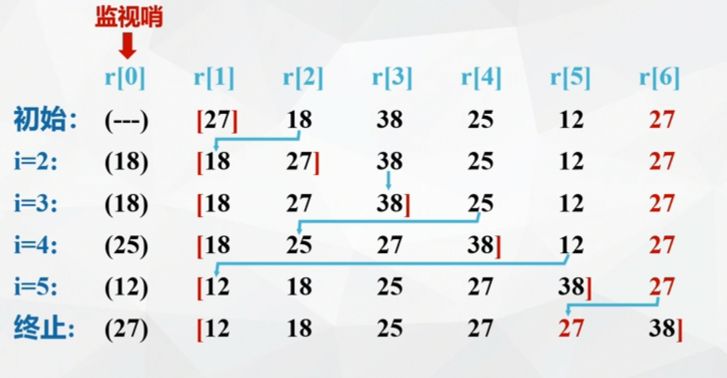
Performance analysis of direct insertion sorting algorithm:

Only one recording auxiliary space is required

Time complexity: depends on the number of comparisons and moves O(n*n)

Binary Insertion Sort

void BInsertSort (SqList &L){
	for(int i=2;i<=L.length;++i){
		L.r[0] = L.r[i];
		low = 1;
		high = i -1;
		while(low<=high){
			m = (low+high)/2;
			if(L.r[0].key<L.r[m].key)
				high = m-1;
			else
				low = m+1;
		}
		for(int j=i-1;j>=high+1;--j)
			L.r[j+1] = L.r[j];
		L.r[high+1]=L.r[0];
	}
}//stable

Although half search sorting can reduce the number of comparisons in keywords to O(nlogn), the number of moves and auxiliary space of records have not changed, so the time complexity is still O(n*n).

Shell Sort

Two features of improved insertion sorting

1. When the sequence to be arranged is "positive sequence", the time complexity is O(n)
2. When the value of n is very small, the efficiency is also high

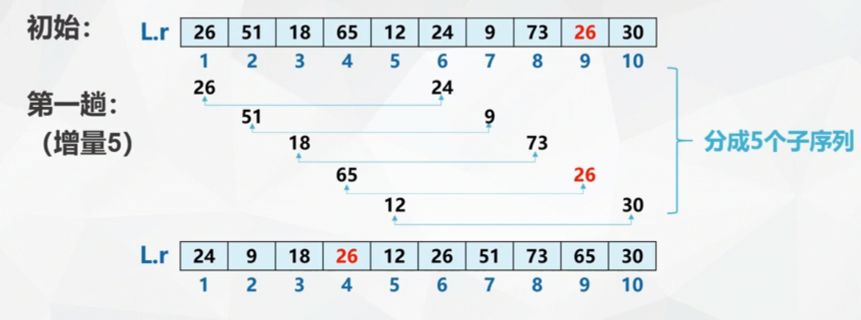
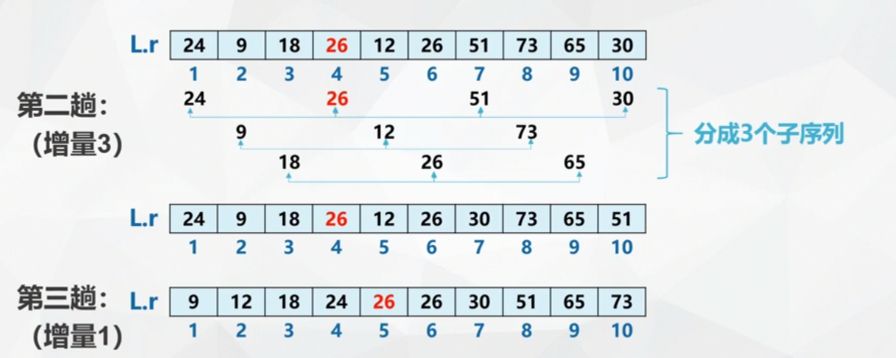
Hill sort, also known as "reduced incremental sort" (unstable)

Basic idea:

1. Firstly, the whole sequence is divided into several subsequences according to a certain increment for direct insertion sorting
2. Reduce the increment, divide the sequence into larger and more orderly subsequences, and then directly insert and sort them respectively
3. This is repeated until the whole sequence is "basically ordered", and then all records (increment 1) are inserted and sorted once

void ShellInsert(SqList &L,int dk){
	for(int i=dk+1;i<=L.length;++i)
		if(L.r[i].key<L.r[i-dk].key){
			L.r[0]=L.r[i];
			for(int j=i-dk;j>0&&L.r[0].key<L.r[j].key;j-=dk)
				L.r[j+dk] = L.r[j];	//Move back
			L.r[j+dk]=L.r[0];
		}
}

void ShellSort(SqList &L,int dlta[],int t){
	//Sort sequential Table L by incremental sequence dlta[0...t-1].
	for(int k = 0;K<t;++k){
		ShellInsert(L,dlta[k])
	}
}

Hill sort performance analysis: when n tends to infinity, the time complexity can be reduced to o (the logarithm of the square of n based on 2)

Exchange sort

bubble sort

Basic idea: compare the keywords of adjacent records in pairs. If they are in reverse order, they will be exchanged until there is no reverse order position.

void bubble_Sort(int a[],int n){
	for(int i = 1;i<n;i++){
		for(int j = n-1;j>=i;j--)  //Blister from back to front
			if(a[j]>a[j+1]){
				int temp = a[j];
				a[j] = a[j+1];
				a[j+1] = a[j];
			}
	}
}

Algorithm optimization:

void bubble_Sort(int a[],int n){
	//Bubble sort the sequence table a
	for(int i = 1,change = TURE;i<=n&&change;i++){
		change = FALSE;
		for(j=n-1;j>=i;--j)
			if(a[j]>a[j+1]){
				int temp = a[j];
				a[j] = a[j+1];
				a[j+1] = a[j];
				change = TRUE;
			}
	}
}

Bubble sorting performance analysis:

Only one recording auxiliary space is required

Time complexity: the slowest in O(n*n) simple sorting

Quick sort

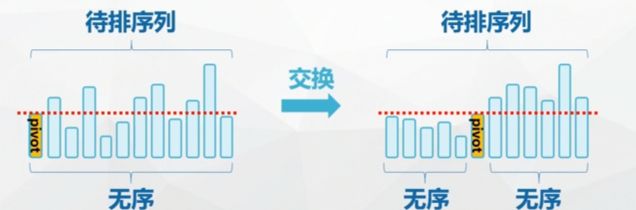
Divide and conquer strategy:

Sub: divide the sequence to be arranged into two independent parts

Rule: quickly sort these two parts recursively

Combination: the whole sequence is orderly

Quick sort idea:

1. Select any record K as the hub (or fulcrum, prvot)

2. One pass quick sorting / Division: divide the remaining records into two subsequences L and R through a series of exchanges, so that the keywords of all records in L are not greater than K, and the keywords of all records in R are not less than K

3. L and R are sorted recursively.
   

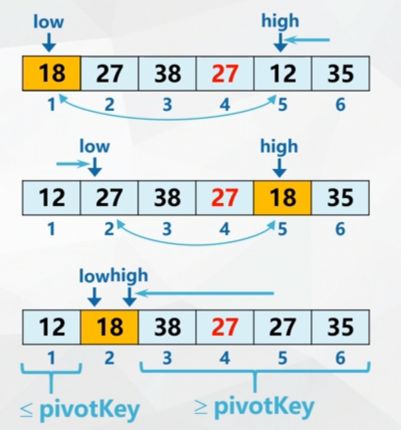
Quick division method:

Two pointers low and high are attached, and the initial value wind points to the first and last records of the sequence.

Set the keyword of pivot record as pivotKey, then:

1. high search forward to find the first record whose keyword is less than pivotKey and exchange with pivot
2. low search backward to find the first record whose keyword is greater than pivotKey and exchange with pivot
3. Repeat steps 1 and 2 until low==high

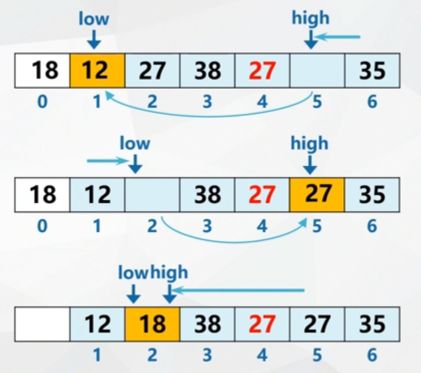
Optimization of fast partition method

Move out: temporarily store the pivot record to position 0

Scan:

1. high search forward to find the first record whose keyword is less than pivotKey and move it to the position indicated by low.
2. low searches backward to find the first record whose keyword is greater than pivotKey and moves it to the position indicated by high.
3. Repeat steps 1 and 2 until low==high.

Classify as: move the pivot record to the position indicated by low

Fast partition algorithm:

int Partition(SqList &L,int low,int high){
	//Exchange the records of sub table r[low...high] in sequence table L, and record the pivot in place
	//And return to its location. At this time, the records before (after) it are not larger (smaller) than it
	L.r[0]=L.r[low];	//Use the first record of the sub table as the pivot record
	pivotkey = L.r[low].key; //Pivot record key
	while(low < high){
		while(low<high&&L.r[high].key>=pivotkey)
			--high;
		L.r[low]=L.r[high];	//Move records smaller than pivot records to the low end
		while(low<high&&L.r[high].key<=pivotkey)
			++low;
		L.r[high]=L.r[low];//Move records larger than pivot records to the high end
	}
	L.r[low]=L.r[0];	//Pivot record in place
	return low; //Return to pivot position
}

Example: the whole process of quick sort

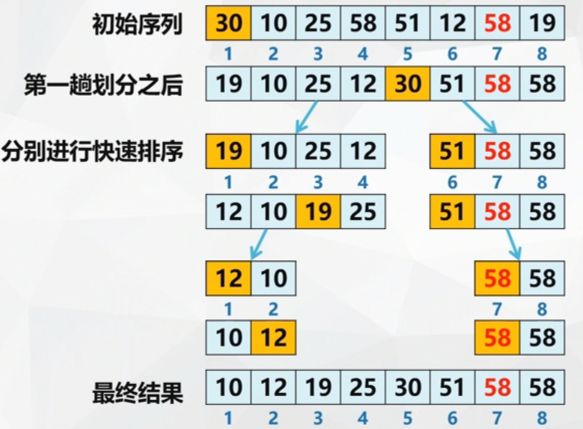
Quick sort algorithm:

void QSort(SqList &L,int low,int high){
	//Quickly sort the subsequence L.r[low..high] in the order table L
	if(low < high){
		//Length greater than 1
		pivotloc = Partition(L,low,high);//Divide L.r[low...high] into two
		QSort(L,low,pivotloc-1);//For recursive sorting of low sub tables, pivot LOC is the pivot position
		QSort(L,pivotloc+1,high);//Recursive sorting of high child tables
	}
}

void Quicksort(SqList &L){
	//Quick sort of sequence table L
	QSort(L,1,L.length)
}

Quicksort performance analysis:

Among all O(nlogn) level sorting methods, quick sorting has the smallest constant factor. At present, it is considered to be an internal sorting algorithm with the best average performance.

Improvement of quick sorting algorithm:

Change the pivot record selection strategy to reduce the worst-case probability

1. Random method: select a record at random

2. The middle of the three:

   (1) low, high and mid take the middle value

   (2) select three at random and take the middle value

3. Hybrid sorting strategy

Select sort

Basic idea of selection sorting:

1. Trip I: select the record with the smallest (largest) keyword among n-i+1(i=1,2,3..., n-1) records as the I (n-i+1) record in the ordered sequence.

2. The sequence to be sorted is divided into two parts: the front is orderly and the rear is disordered

   Initial: no records at the front and all n records at the rear

   Select the record with the smallest keyword from the back of each trip and expand it to the front

Simple selection sort

Also known as direct selection sort, it is a sort in place.

Trip I: select the record with the smallest keyword from n-i+1 records through n-i(i=1,2,3... n-1) keyword comparison, and exchange with the ith record.

void SersctSort(SqList &L){
	int i,j,min;	
	for(i=1;i<L.length;i++){		
		min = i;		
		for(j=i+1;j<=L.length;j++){			
			if(L.r[min]>L.r[j])				
			min=j;		
		}
	}	
	if(i!=min){		
		int temp = l.[i];		
		L.[i] = L.[min];		
		L.[min] = L.[i];	
	}
}

Quicksort performance analysis: O(n*n)

Disadvantages of simple selection sorting:

The main operation of selecting sorting: comparison between keywords

Simple selection sorting failed to make full use of the results of the previous comparison

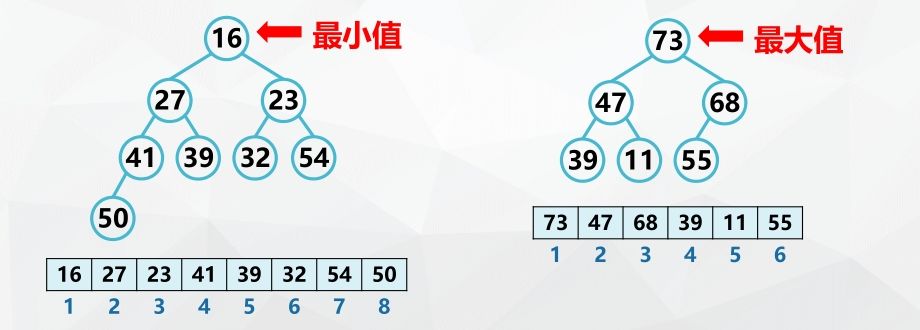
Tree Selection Sort

Basic idea of tree sorting:

Also known as tournament ranking

Firstly, the keywords of n records are compared;

Then, a pairwise comparison is made between [n/2] smaller ones;

Repeat until the record with the smallest keyword is selected.

Winner tree

• Complete binary tree with n leaf nodes
• Leaf (external node) - all n records to be sorted
• Internal node -- the winner in pairwise comparison
• Root - the record with the smallest keyword

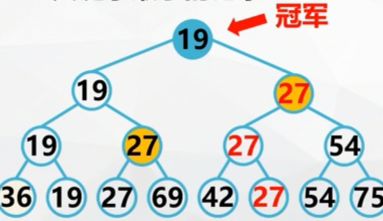
Replace the minimum keyword in the leaf node with "maximum", and modify the node from the leaf node to the root path.

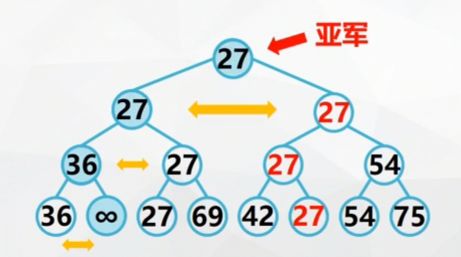
And so on

Performance analysis of tree selection sorting:

Time complexity O(nlogn)

Spatial complexity O(n)

Heap sort

Disadvantages of tree selection sorting:

1. Need more auxiliary space
2. Redundant comparison with "maximum"

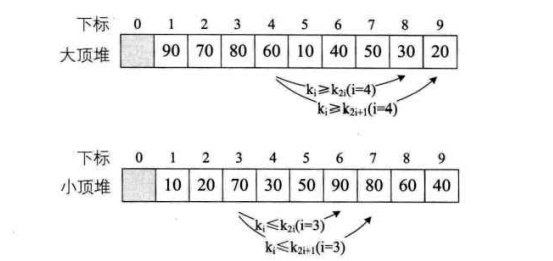
Definition of heap:

The sequence {K1,K2,..., Kn} of n elements is a heap if and only if the following relationship is satisfied

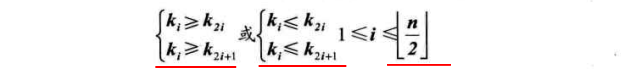
If the one-dimensional array corresponding to this sequence is regarded as a complete binary tree, the meaning of heap indicates that the values of all non terminal nodes in the complete binary tree are not greater than (or less than) the values of their left and right child nodes.

The heap top element must be the minimum (maximum) of n elements in the sequence

Basic idea of heap sorting

1. The column to be sorted is constructed into a large top heap, and the top is the maximum value of the whole sequence;

2. Trip I: after removing the top of the heap, readjust the remaining n-i elements to a large top heap to obtain the whole I maximum values;

   (in fact, it is exchanged with the end element of the heap array. At this time, the end element is the maximum value)

3. Repeat step 2 to get an ordered sequence.

Question 1:

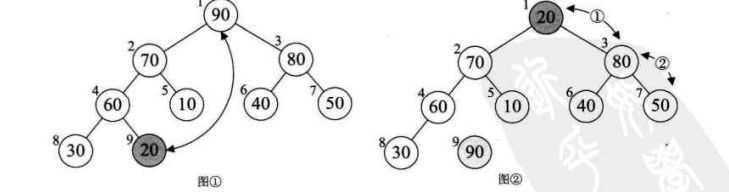
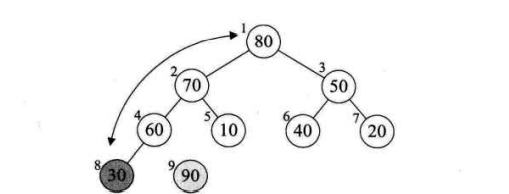
After removing the top of the heap (i.e. exchanging it with the n-i+1 element), how to readjust the remaining n-i elements to a large top heap?

Note: only the new top heap element does not conform to the heap definition.

Solution: "screening", that is, an adjustment process from the top of the heap to the leaves: compare the left and right children, select the larger one, and then compare with the node. If the node is small, exchange the older child with the node, and then make the next level comparison.

Filtering algorithm:

typedef SqList HeapType; //Heap is represented by sequential table storage
void HeapAdjust(HeapType &H,int s,int m){
    //The keywords recorded in H.r[s...m] are known except H.R [S] All except key meet the definition of heap
    //This function adjusts the position of H.r[s] so that H.r[s...m] becomes a large top heap
    rc = H.r[s]
    for(j=2*s;j<=m;j*=2){ //Filter down the child nodes with larger key s
        if(j<m&&H.r[j].key<H.r[j+1].key)	
            ++j;		  //j is the subscript of the record with larger key
        if(rc.key>=H.r[j].key)	//rc should be inserted in position s
            break;
        H.r[s] = H.r[j];
        s=j;
    }
    H.r[s]=rc;	//insert
}

Question 2:

How to construct an unordered sequence into a heap?

Note: leaves must meet the heap definition

Solution: start from the last non terminal node (element [n/2]) and "filter" one by one

Heap sorting algorithm:

void HeapSort(HeapType &H){
	//Heap sort sequence table H
	for(i=H.length/2;i>0;--i)
		HeapAdjust(H,i,H.length);
	for(i=H.length;i>1;--i){
		temp = H.r[1];
		H.r[1]=H.r[i];
		H.r[i]=H.r[1];
		HeapAdjust(H,1,i-1); 
	}
}

Heap sort performance analysis: time complexity O(nlogn)

• It is insensitive to the initial sequence, and the best, worst and average time complexity are O(nlogn)
• Only one secondary storage space is required
• instable
• The number of comparisons required for initial reactor building is too many, which is not suitable for the case of small sequence length

Merge sort

Basic idea of merging and sorting:

Merge: combine two or more ordered tables into a new ordered table

Merge sort: a sort method implemented by using the idea of merge

2-way merge sort:

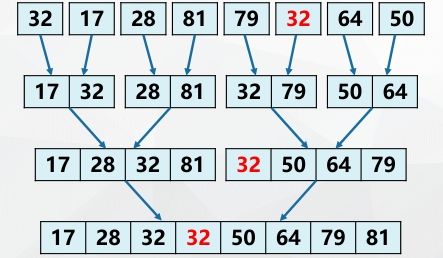
Algorithm: merge two adjacent ordered sequences

void Merge(RcdType SR[],RcdTypest &TR[],int i,int m,int n){
	//Merge ordered SR[i...m] and SR[m+1...n] into ordered TR[i..n]
	for(j=m+1,k=i;i<=m&&j<=n;++k){
		//Incorporate the records in SR from small to large into TR
		if(SR[i].key<SR[i].key)
			TR[k]=SR[i++];
		else
			TR[k]=SR[j++];
		if(i<=m)
		{
        	for(l=0;l<m-i;l++)
				TR[k+l]=SR[i+l]; //Copy remaining SR[i...m] to TR
		}
		if(j<=n)
		{
        	for(l=0;l<n-j;l++)
				TR[k+l]=SR[j+l]; //Copy remaining SR[j...n] to TR
		}
        
	}
}

Recursively implement 2-way merge sorting:

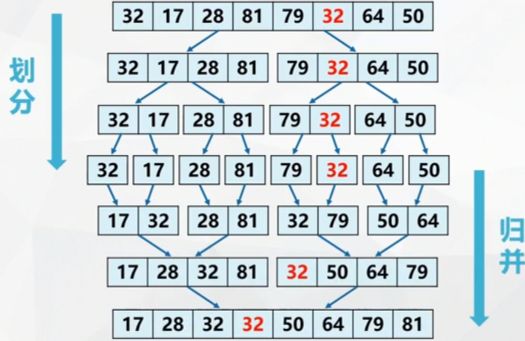
[the external chain image transfer fails. The source station may have an anti-theft chain mechanism. It is recommended to save the image and upload it directly (IMG uecjfhhi-16400026290706) (C: \ users \ 1 \ desktop \ 23. JPG)]

void MSort(RcdType SR[],RcdTypest &TR1[],int s,int t){
	//Merge SR[s...t] into TR1[s...t]
	if(s==t)
		TR1[s]=SR[s];
    else{
        m = (s+t)/2;
        MSort(SR,TR2,s,m);
        MSort(SR,TR2,m+1,t);
        Merge(TR2,TR1,s,m,t);
    }
}

void MergeSort(SqList &L){
    MSort(L.r,L.r,1,L.length);
}
        

2-way merge sort performance analysis:

• The time complexity of each merging is O(n)
• [log(2)n] times sorting is required
• The time complexity is O(nlogn)
• The space complexity is O(n)
• stable

Cardinality sort

(learn principles but not implement them)

The first four categories have something in common: Based on the two operations of "keyword comparison" and "record movement".

Cardinality sorting: sort single keywords with the help of the idea of multi keyword sorting.

Multi keyword sorting:

Highest priority method (MSD)

Least squares first (LSD)

Cardinality sorting: the LSD idea in multi keyword sorting is used for single logical keyword sorting.

A single logical keyword is regarded as a composite of several keywords

For example:

Numeric keyword, each digit can be regarded as a keyword

String keyword, the character in each position can be regarded as a keyword

If the value range of each keyword obtained by decomposition is the same, sorting by LSD is more convenient.

The main idea of cardinality sorting:

Storage space required for cardinality sorting:

Assuming a total of N records, keyword K can be divided into d keywords, each of which has a value in RADIX

The implementation of sequential storage requires the auxiliary space of RADIX*N records!

RADIX queues

Each queue needs to reserve storage space for N records

The implementation of chained storage only needs the auxiliary space of N+RADIX*2 pointers!

RADIX single linked list (queue)

Each is provided with a head pointer and a tail pointer

During allocation, only the pointer needs to be modified, and no additional storage space is required

Example: chained storage implements cardinality sorting

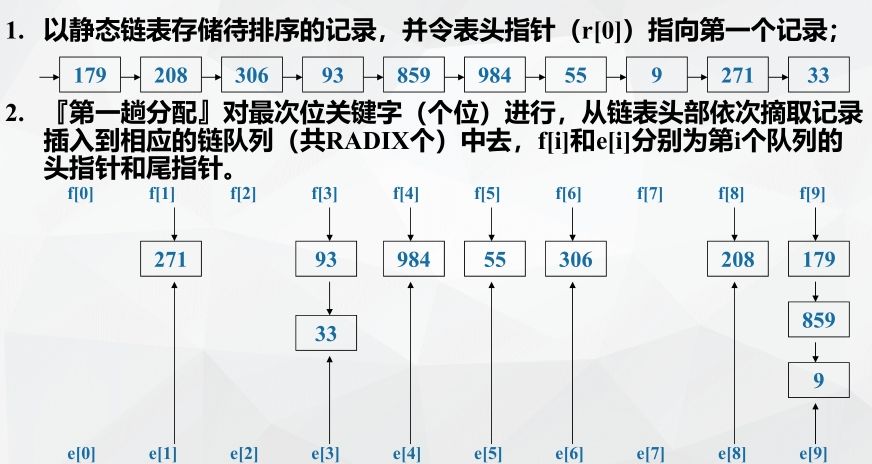
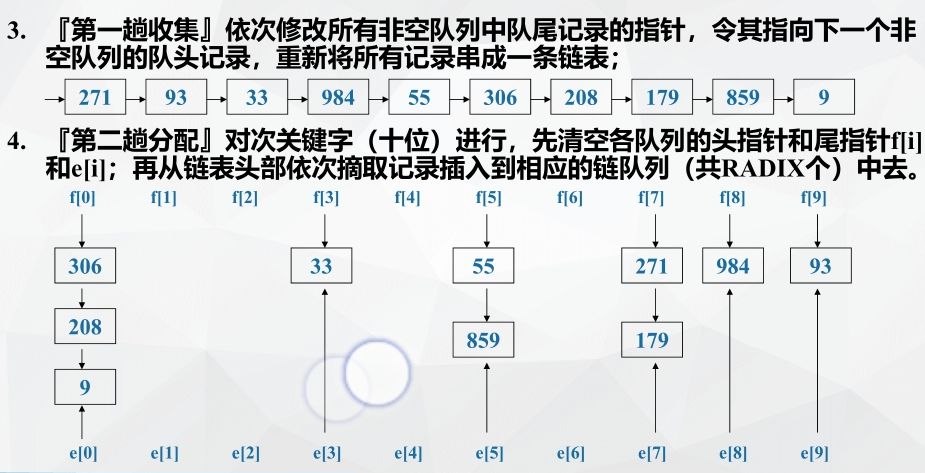
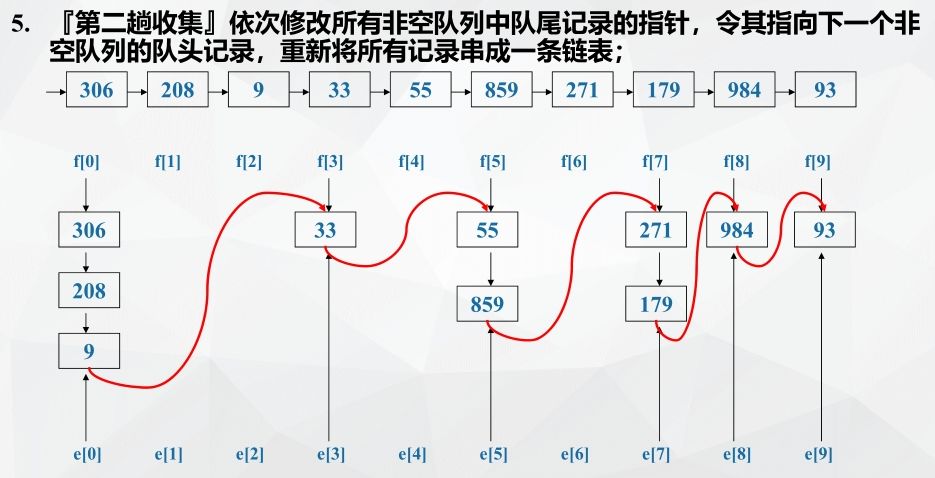
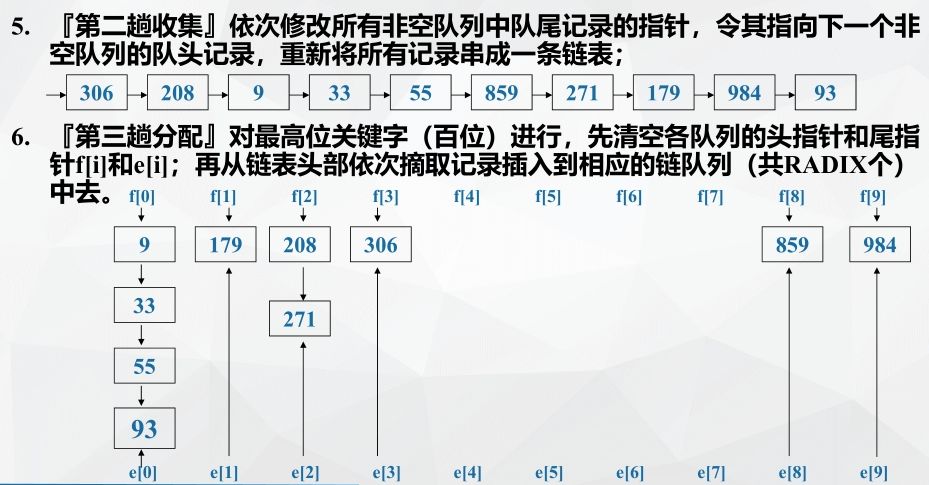
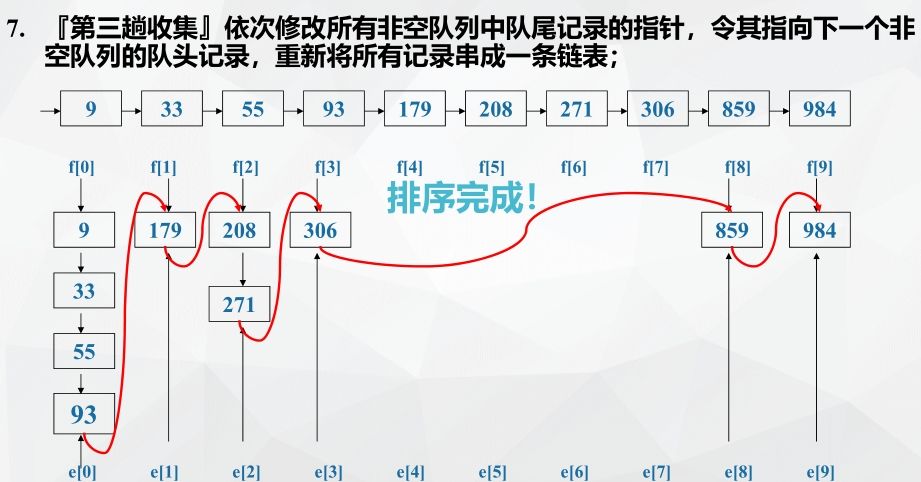
Cardinality sorting performance analysis:

Comparison of various internal sorting methods

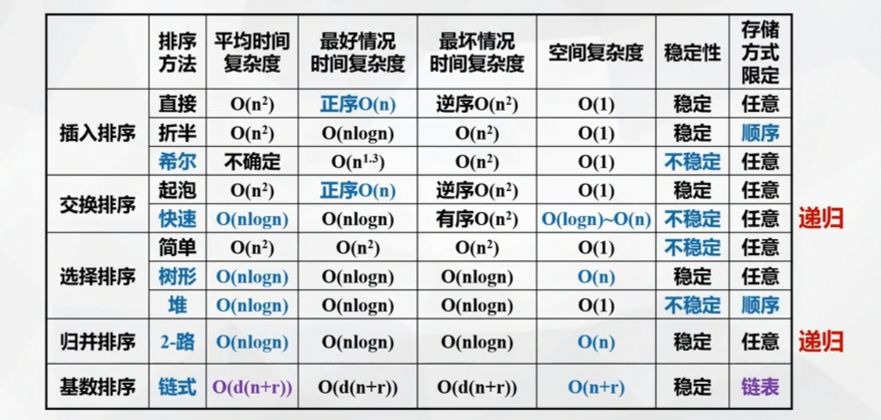
Classification by time complexity:

1. Simple sorting method (average O(n*n)): direct insertion, half insertion, simple selection, bubble sorting

   Direct insertion is most commonly used, especially for sequences that are basically ordered

2. Advanced sorting method (average O(nlogn)): heap sorting, quick sorting, merge sorting, tree selection

   Quick sort is considered to be the best average performance at present

   When the sequence length is large, merge sort is faster than heap sort

3. Between: Hill sort

4. Cardinality sort

Best case, worst case time complexity:

1. Best case: direct insertion and bubble sorting are the best

2. Worst case: heap sort and merge sort are the fastest

3. Average: quick sort

Classification by spatial complexity:

1. O(n): merge sort, cardinal sort
2. O(log(2)n-n): quick sort
3. O(1): direct insert, half insert, simple selection, bubble sort, Hill sort, heap sort

Classification by stability:

1. Stable: direct insertion, half insertion, bubbling insertion, merge insertion, cardinal insertion, tree selection
2. Unstable: simple selection, Hill sort, heap sort, quick sort

When n is not large (< 10 * 1024), a simple sorting method should be adopted

When n is large, advanced sorting method should be adopted

Finally finishing sorting!!!!!!
Individual algorithms are difficult to implement, so they are not written. Forgive me, the final exam will not be too difficult. It is most important to understand the principle.
I wish you all a higher grade at the end of the term!!!