Learn the "Neural Collaborative Filtering". This paper introduces the use of deep neural network to model user item interaction, proposes NCF framework, and instantiates GMF, MLP and NeuMF.
Problems with MF
1. Assuming that all hidden factors are independent of each other, MF can be regarded as a linear model (when doing inner product, the weight of corresponding position is 1), which only deals with shallow features, and the result deviation is large. 2. The hiding factor of MF is not easy to determine. For a complex user item interaction, the effect of low dimension is not good, but for a sparse matrix, increasing the number of hidden factors to high dimension may cause overfit.
NCF framework
The author uses DNNs to construct the NCF framework, models the user item interaction, and uses multi-layer neural network to obtain the predicted value y^ui.
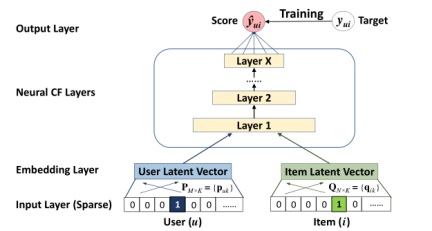
Because it is tested with implicit data (1 indicates interaction, 0 indicates no interaction), the activation function of probability function (sigmoid) is added to the output layer. Therefore, optimize: SGD - log loss.
NeuMF
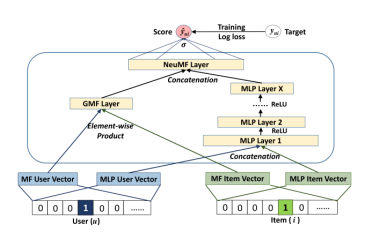
GMF on the left and MLP on the right are integrated as NeuMF.
GMF: MF can be interpreted as a special form (or a linear structure) under the NCF framework. As follows, the formula is: y^ui = aout (hT(pu ⨀ qi)) so that aout is an identity function, and the h vector is 1, which is a typical MF.
MLP: NCF framework combines user feature vector and item feature vector. If the vectors are simply spliced, it can not explain any interaction between user and item implicit features. Therefore, MLP is introduced to extract the interactive information between articles and users. The Action function of MLP layer selects Relu (sigmoid is limited to (0,1), and tanh is the extended version of sigmoid).
During initialization, you can use Adam optimization to pre train GMF and MLP. The pre training parameters are used as the initialization of NeuMF, which is optimized by SGD.
NeuMF model combines the linear of GMF and the nonlinear of MLP to model user item interaction.
Dataset: MovieLens;Pinterest
BaseLInes: ItemPop,ItemKNN,BPR,eALS
Difference between LFM and NCF:
1.LFM decomposes the user item matrix into the implicit matrix of users and items, and NCF constructs a user item interaction model.
2.LFM can only consider the linear relationship between implicit classes (usually nonlinear relationship when there are few implicit factors). NCF can instantiate GMF for linear relationship, and MLP can also be integrated if there is nonlinear relationship.
3.LFM can only complete the user item matrix, and there is a cold start problem for new users and new items. NCF has strong generalization ability and versatility, and can deal with new users or new items. Because there is an embedding layer in the model, it can train the parameters in the mapping layer, which will map new users or new items to an implicit feature vector.
Code implementation effect:
Comparative experimental group:
Parameter setting: dataset: MovieLens;Pinterest batch_size = 256 topK = 10 lr = 0.001 epochs = 10 (The 100 set by the author of the paper doesn't run so much because of the learning model) factors = 8/16/32 layers_num(MLP Number of layers) = 3 GMF,MLP,NeuMF optimizer: Adam GMF,MLP,NeuMF Loss function: BCELoss() Evaluation indicators of each group: HR: Concerned about what users want, do I recommend it and emphasize the "accuracy" of prediction NDCG: Care about whether the items found are placed in a more prominent position of the user, that is, emphasize "order"“ stay MovieLens On dataset(4970845 pieces of data in the training set and 6040 pieces of data in the verification set): 1. factors = 8 : GMF,MLP,NeuMF_pre,NreMF_unPre 2. factors = 16: GMF,MLP,NeuMF_pre,NreMF_unPre 3. stay GMF Upper: factors = 8 ,16 ,32 4. stay MLP Upper: factors = 8 ,16 ( MLP The training time was quite long and there was no test factors=32) 5. stay NeuMF_pre: factors = 8 ,16 (because MLP of factors=32 No test, so NeuMF No initialization parameters) 6. stay NeuMF_unpre: factors = 8 ,16 (because MLP of factors=32 No test, so NeuMF No initialization parameters) stay Pinterest On dataset(7041970 data in the training set and 55187 data in the verification set): 1. factors = 8 : GMF,MLP,NeuMF_pre
In my computer, 10 epochs run for almost 30-40 minutes.
On the MovieLens dataset:
-
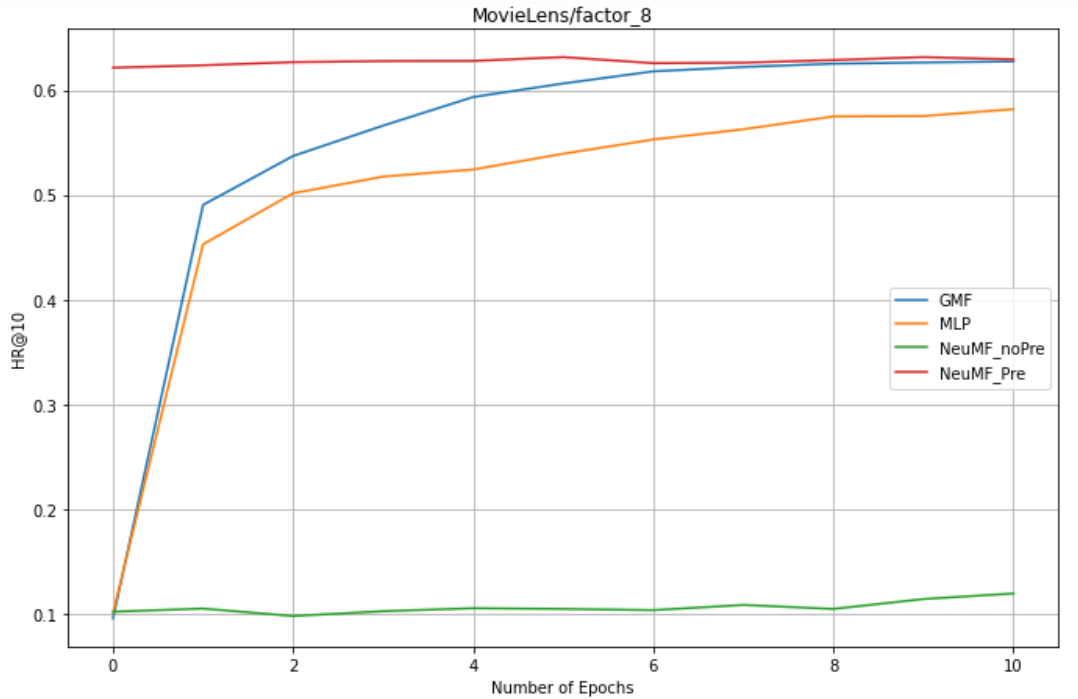
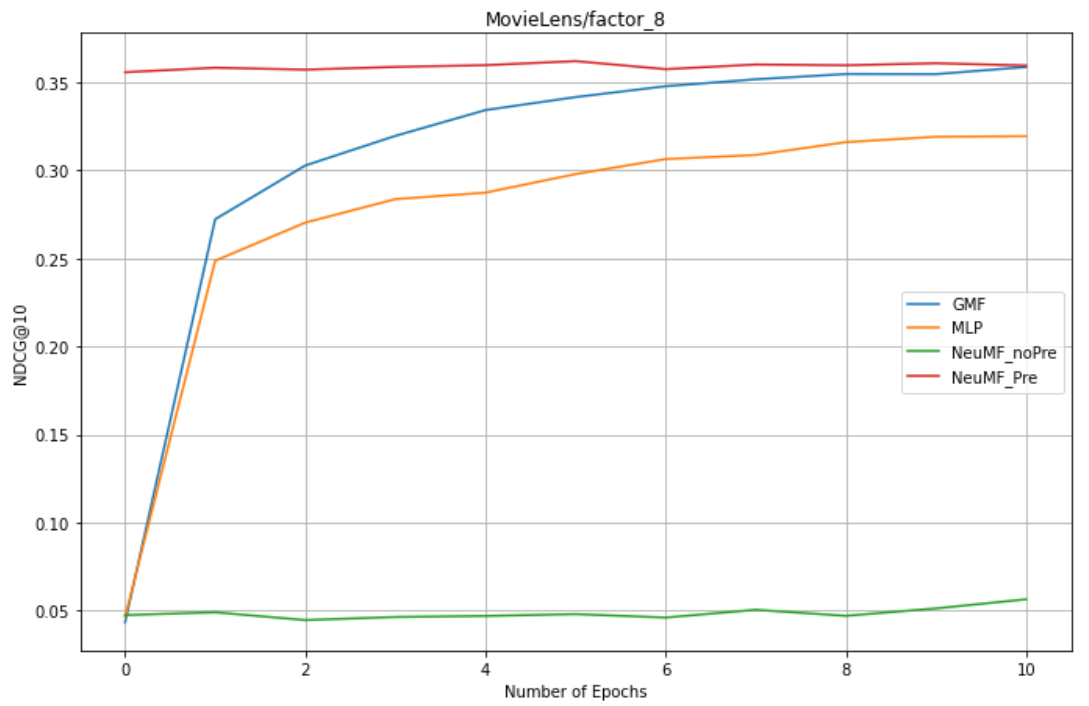
factors = 8 : GMF,MLP,NeuMF_pre,NreMF_unPre
-
factors = 16: GMF,MLP,NeuMF_pre,NreMF_unPre
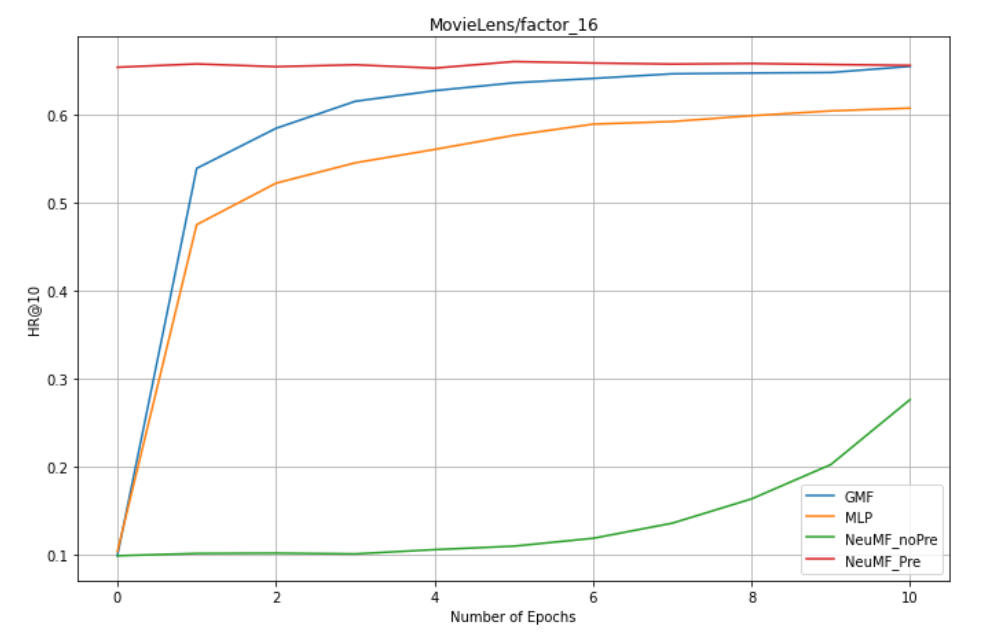
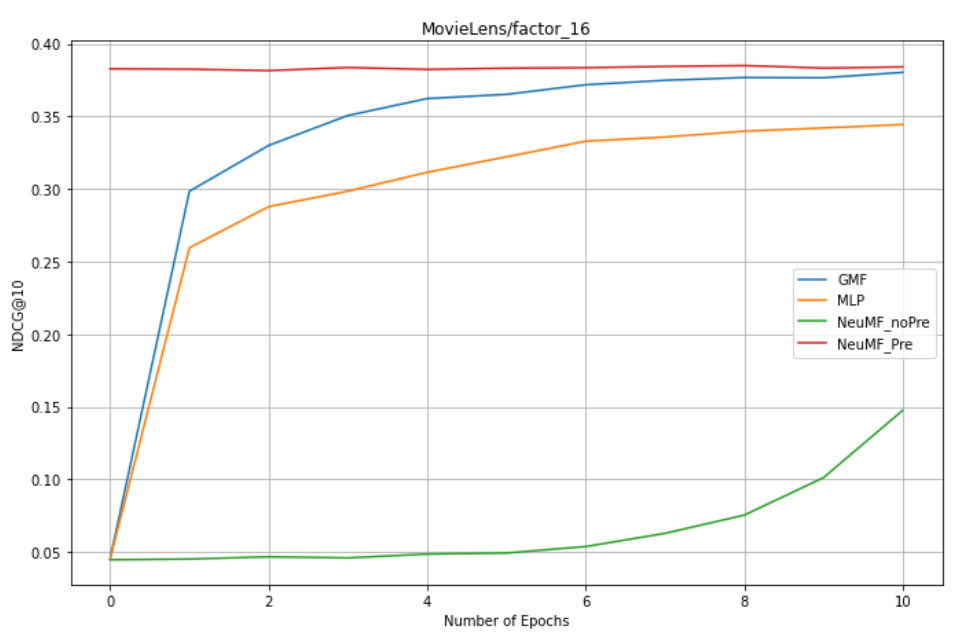
-
On GMF: factors = 8, 16, 32
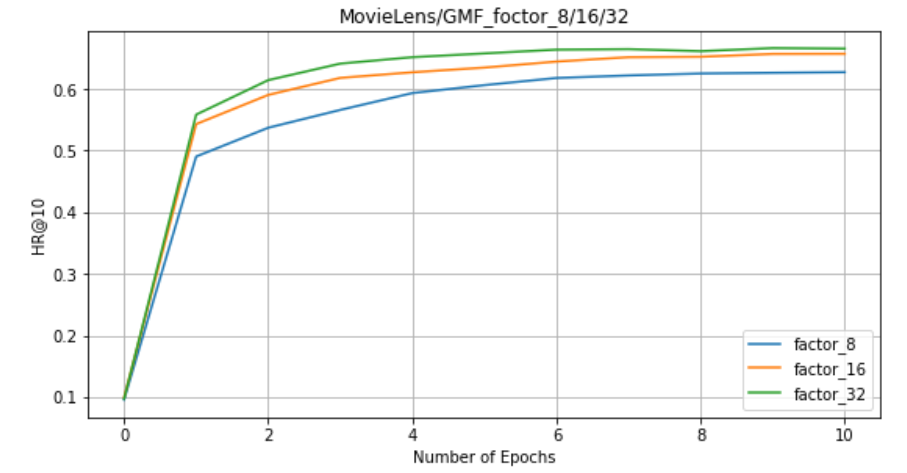
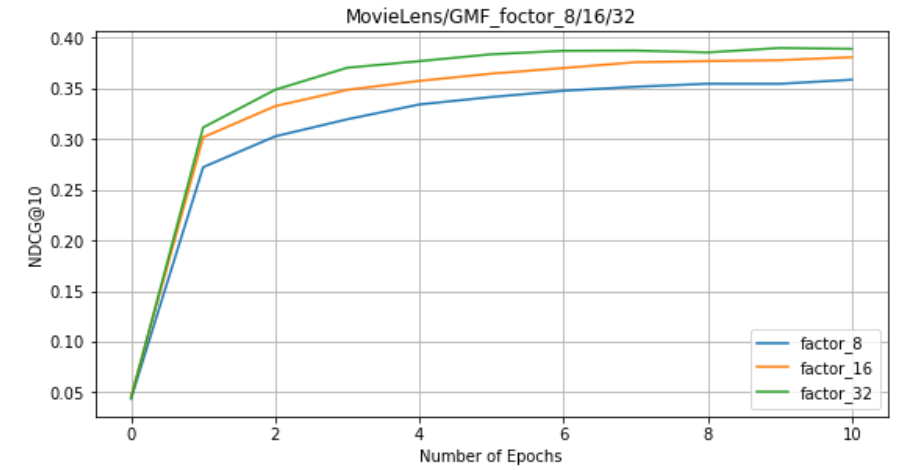
-
On MLP: factors = 8, 16 (MLP training time is relatively long, no measured factors=32)
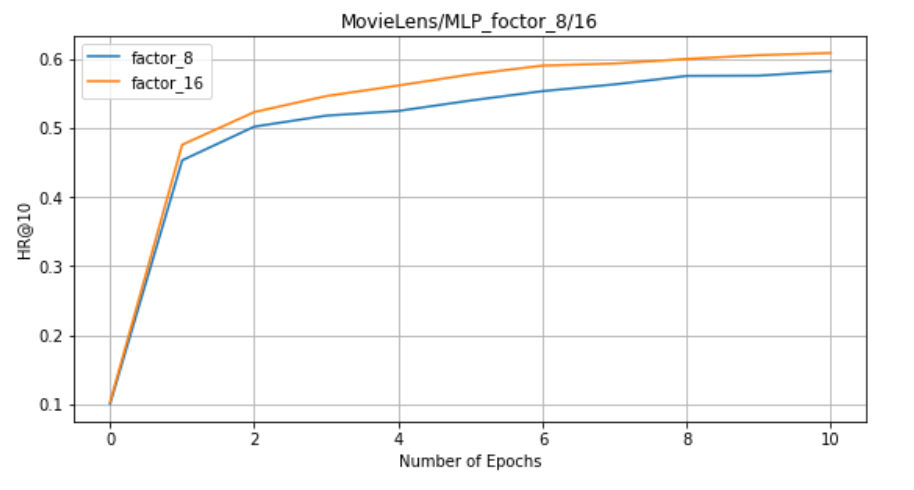
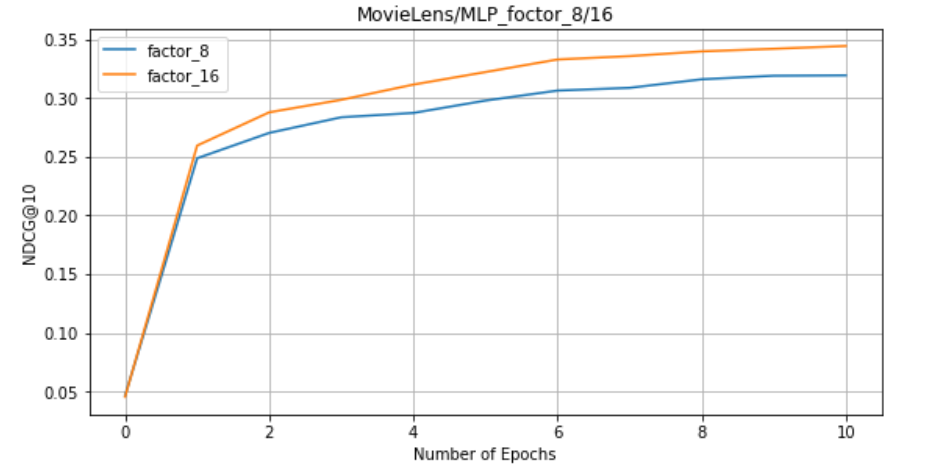
-
In NeuMF_pre: factors = 8, 16 (there is no NeuMF initialization parameter because MLP factors=32 is not measured)
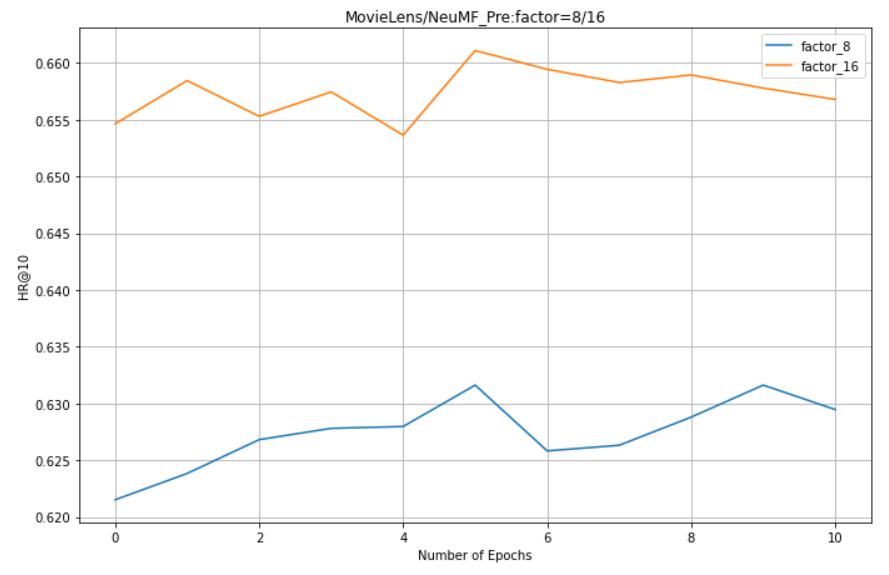
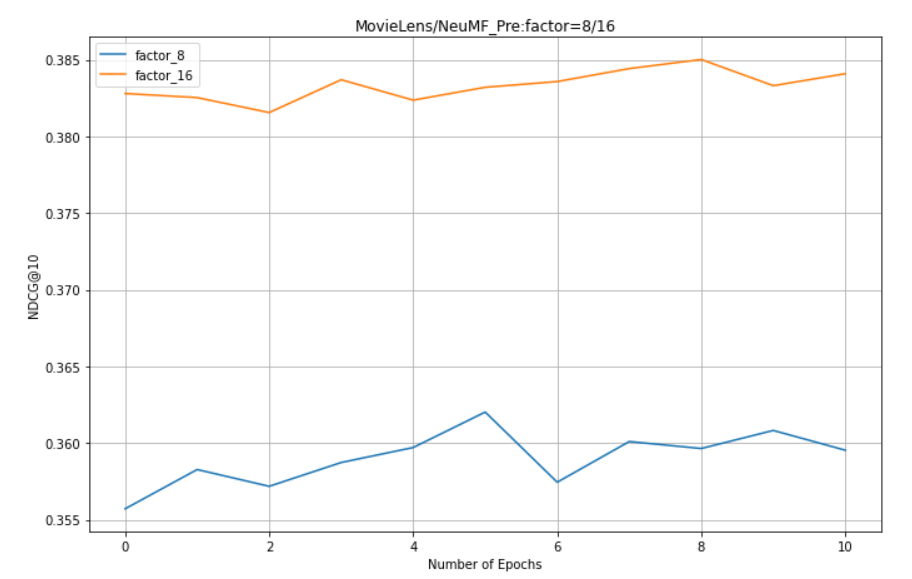
-
In NeuMF_unpre: factors = 8, 16 (because factors=32 of MLP is not measured, NeuMF initialization parameters do not exist)
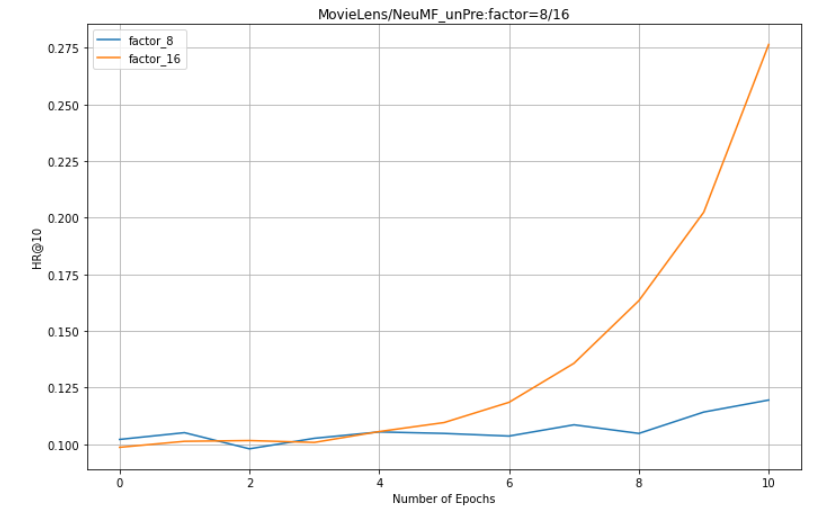
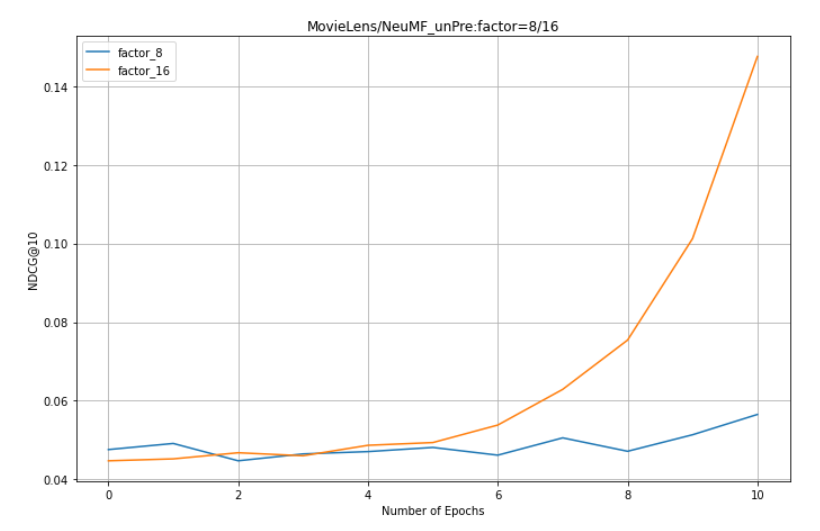
On the Pinterest dataset:
1. factors = 8 : GMF,MLP,NeuMF_pre
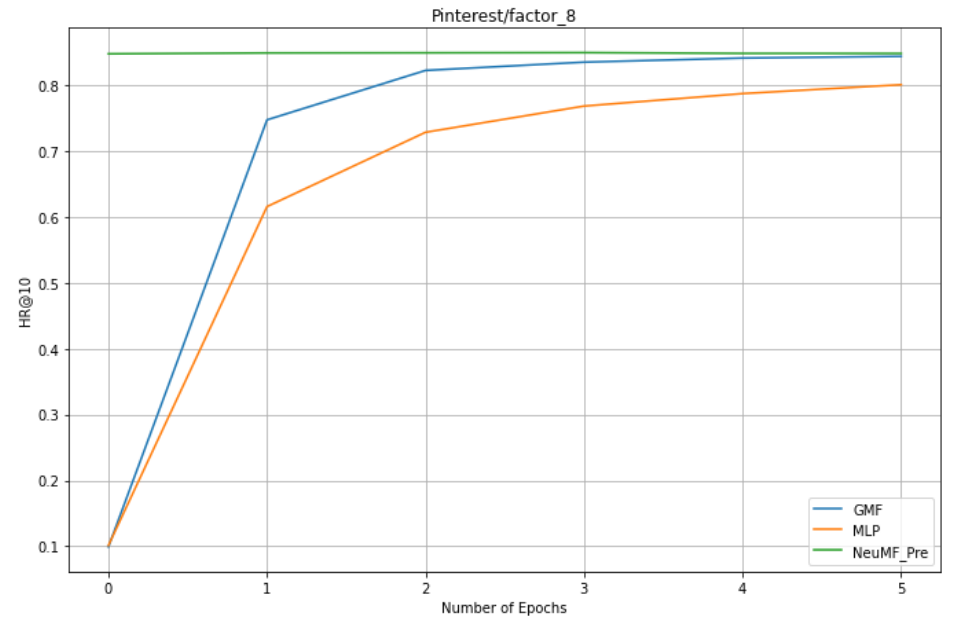
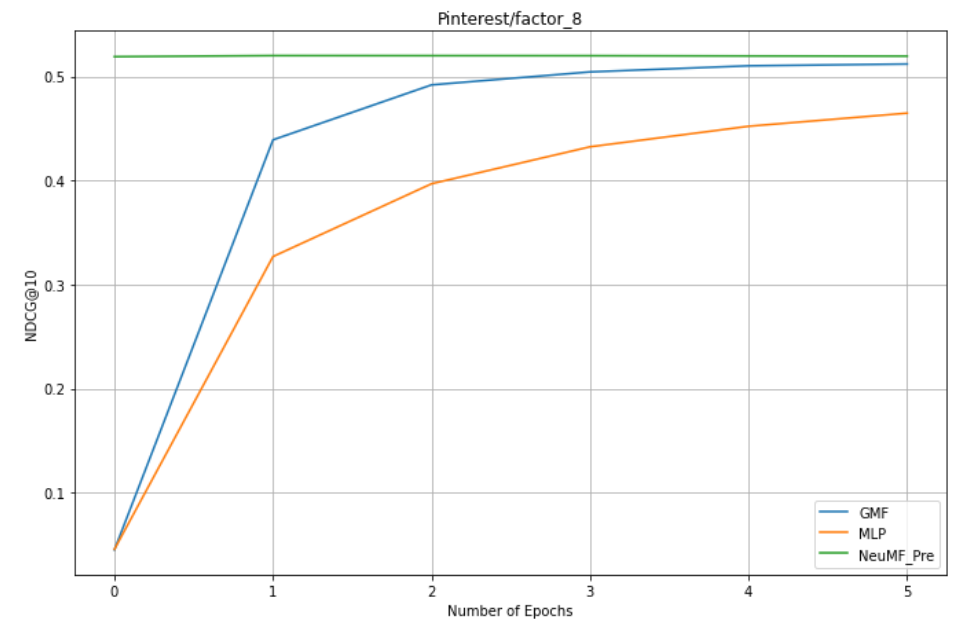
Conclusion:
1. NeuMF effect of pre training is better than GMF and MLP (combining linear GMF and nonlinear MLP)
2. NeuMF without pre training needs more epochs to get good results.
3.GMF is better than MLP
4. The larger the dataset (Pinterest is nearly twice as large as MovieLens dataset), the better the effect.
5. For NeuMF, GMF and MLP, the larger the factor, the better the effect.
Main code:
Load dataset:
def load_data():
#train_mat
train_data = pd.read_csv('Data/ml-1m.train.rating',sep='\t',header=None,
names=['user','item'],usecols=[0,1],dtype={0: np.int32, 1: np.int32})
user_num = train_data['user'].max() + 1
item_num = train_data['item'].max() + 1
train_data = list(train_data.values)
train_mat = sp.dok_matrix((user_num,item_num),dtype=np.float32)
for x in train_data:
train_mat[x[0],x[1]] = 1.0
#testRatings
ratingList = []
with open('Data/ml-1m.test.rating', "r") as f:
line = f.readline()
while line != None and line != "":
arr = line.split("\t")
user, item = int(arr[0]), int(arr[1])
ratingList.append([user, item])
line = f.readline()
#testNegatives
negativeList = []
with open('Data/ml-1m.test.negative', "r") as f:
line = f.readline()
while line != None and line != "":
arr = line.split("\t")
negatives = []
for x in arr[1: ]:
negatives.append(int(x))
negativeList.append(negatives)
line = f.readline()
return train_mat, ratingList, negativeList
train_mat, testRatings, testNegatives = load_data()
user_num, item_num = train_mat.shape
train_mat, testRatings, testNegatives = load_data()
train_mat is the training matrix, and negative sampling is also required; testrates and testNegatives are the two list s used in our evaluation of indicators, testrates is the evaluation sample, and testNegatives depends on whether testrates appear (HR) and where they appear (NDCG).
Negative sampling:
def get_train_instances(train, num_negatives = 4, num_item = item_num):
user_input, item_input, labels = [], [], []
for (u,i) in train.keys():
#positive instance
user_input.append(u)
item_input.append(i)
labels.append(1)
#negative instance
for t in range(num_negatives):
j = np.random.randint(num_item)
while u in train.keys() and j in train:
j = np.random.randint(num_item)
user_input.append(u)
item_input.append(j)
labels.append(0)
return user_input,item_input,labels
user_num, item_num = train_mat.shape #Results after loading negative samples user_input,item_input,labels = get_train_instances(train_mat) #The matrix is transferred to Tensor. Note that the embedding layer must be LongTensor user_input = np.array(user_input) user_input = torch.LongTensor(user_input) item_input = np.array(item_input) item_input = torch.LongTensor(item_input) labels = np.array(labels) labels = torch.FloatTensor(labels) user_input = user_input.reshape(-1,1) item_input = item_input.reshape(-1,1) labels = labels.reshape(-1,1) #To split the data, concat enate it train_Data = torch.cat((user_input,item_input),1) train_Data = torch.cat((train_Data,labels),1) #batch_size = 256, data_train is the training set data_train = Data.DataLoader(dataset = train_Data, batch_size = 256, shuffle = True)
Evaluation indicators: HR, NDCG
_model = None
_testRatings = None
_testNegatives = None
_K = None
def evaluate_model(model, testRatings, testNegatives, K, num_thread):
"""
HR,NDCG
"""
global _model
global _testRatings
global _testNegatives
global _K
_model = model
_testRatings = testRatings
_testNegatives = testNegatives
_K = K
hits, ndcgs = [],[]
for idx in range(len(_testRatings)):
(hr,ndcg) = eval_one_rating(idx)
hits.append(hr)
ndcgs.append(ndcg)
return (hits, ndcgs)
def eval_one_rating(idx):
rating = _testRatings[idx]
items = _testNegatives[idx]
u = rating[0]
gtItem = rating[1]
items.append(gtItem)
# Get prediction scores
map_item_score = {}
users = np.full(len(items), u, dtype = "int64")#Fill a length of len (items) with u
predictions = _model.forward(torch.LongTensor(users), torch.LongTensor(np.array(items)))
for i in range(len(items)):
item = items[i]
map_item_score[item] = predictions[i]
items.pop()
# Evaluate top rank list
ranklist = heapq.nlargest(_K, map_item_score, key=map_item_score.get)#Find the maximum number of 10
hr = getHitRatio(ranklist, gtItem)
ndcg = getNDCG(ranklist, gtItem)
return (hr, ndcg)
def getHitRatio(ranklist, gtItem):
for item in ranklist:
if item == gtItem:
return 1
return 0
def getNDCG(ranklist, gtItem):
for i in range(len(ranklist)):
item = ranklist[i]
if item == gtItem:
return math.log(2) / math.log(i+2)#Prevent denominator from being 0
return 0
HR = [] NDCG = [] (hits, ndcgs) = evaluate_model(GMF_model, testRatings, testNegatives, topK, evaluation_threads) hr, ndcg = np.array(hits).mean(), np.array(ndcgs).mean() HR.append(hr) NDCG.append(ndcg)
GMF model:
class GMF(nn.Module):
def __init__(self, user_num, item_num, factor_num):
super(GMF, self).__init__()
"""user_num: Number of users item_num: Number of items factor_num: Mapping dimension """
self.embed_user_GMF = nn.Embedding(num_embeddings = user_num,embedding_dim = factor_num,norm_type=2)
self.embed_item_GMF = nn.Embedding(item_num,factor_num)
self.predict_layer = nn.Linear(factor_num, 1)
self._init_weight_()
def _init_weight_(self):
#Generate values from the normal distribution N(mean, std) of the given mean and standard deviation, and fill in the input tensor or variable
nn.init.normal_(self.embed_user_GMF.weight,std=0.01)
nn.init.normal_(self.embed_item_GMF.weight,std=0.01)
def forward(self, user, item):
embed_user_GMF = self.embed_user_GMF(user)
embed_item_GMF = self.embed_item_GMF(item)
#inner product
output_GMF = embed_user_GMF * embed_item_GMF
prediction = torch.sigmoid(self.predict_layer(output_GMF))
return prediction.view(-1)
MLP model:
class MLP(nn.Module):
def __init__(self, user_num, item_num, factor_num, num_layers, dropout):
super(MLP, self).__init__()
self.embed_user_MLP = nn.Embedding(user_num, factor_num * (2 ** (num_layers - 1)))
self.embed_item_MLP = nn.Embedding(item_num, factor_num * (2 ** (num_layers - 1)))
MLP_modules = []
for i in range(num_layers):
input_size = factor_num * (2 ** (num_layers - i))
MLP_modules.append(nn.Dropout(p=dropout))
MLP_modules.append(nn.Linear(input_size, input_size//2))
MLP_modules.append(nn.ReLU())
self.MLP_layers = nn.Sequential(*MLP_modules)
self.predict_layer = nn.Linear(factor_num, 1)
self._init_weight_()
def _init_weight_(self):
nn.init.normal_(self.embed_user_MLP.weight, std=0.01)
nn.init.normal_(self.embed_item_MLP.weight, std=0.01)
for m in self.MLP_layers:
if isinstance(m, nn.Linear):
nn.init.xavier_uniform_(m.weight)
nn.init.kaiming_uniform_(self.predict_layer.weight,a=1, nonlinearity='sigmoid')
def forward(self, user, item):
embed_user_MLP = self.embed_user_MLP(user)
embed_item_MLP = self.embed_item_MLP(item)
interaction = torch.cat((embed_user_MLP, embed_item_MLP), -1)
output_MLP = self.MLP_layers(interaction)
prediction =torch.sigmoid(self.predict_layer(output_MLP))
return prediction.view(-1)
NeuMF model:
class NeuMF(nn.Module):
def __init__(self, user_num, item_num, factor_num, num_layers,
dropout, model, GMF_model=None, MLP_model=None):
super(NeuMF, self).__init__()
"""
user_num: number of users;
item_num: number of items;
factor_num: number of predictive factors;
num_layers: the number of layers in MLP model;
dropout: dropout rate between fully connected layers;
model: 'MLP', 'GMF', 'NeuMF-end', and 'NeuMF-pre';
GMF_model: pre-trained GMF weights;
MLP_model: pre-trained MLP weights.
"""
self.dropout = dropout
self.model = model
self.GMF_model = GMF_model
self.MLP_model = MLP_model
self.embed_user_GMF = nn.Embedding(user_num, factor_num)
self.embed_item_GMF = nn.Embedding(item_num, factor_num)
self.embed_user_MLP = nn.Embedding(
user_num, factor_num * (2 ** (num_layers - 1)))
self.embed_item_MLP = nn.Embedding(
item_num, factor_num * (2 ** (num_layers - 1)))
MLP_modules = []
for i in range(num_layers):
input_size = factor_num * (2 ** (num_layers - i))
MLP_modules.append(nn.Dropout(p=self.dropout))
MLP_modules.append(nn.Linear(input_size, input_size//2))
MLP_modules.append(nn.ReLU())
self.MLP_layers = nn.Sequential(*MLP_modules)
if self.model in ['MLP', 'GMF']:
predict_size = factor_num
else:
predict_size = factor_num * 2
self.predict_layer = nn.Linear(predict_size, 1)
self._init_weight_()
def _init_weight_(self):
""" We leave the weights initialization here. """
if not self.model == 'NeuMF-pre':
nn.init.normal_(self.embed_user_GMF.weight, std=0.01)
nn.init.normal_(self.embed_user_MLP.weight, std=0.01)
nn.init.normal_(self.embed_item_GMF.weight, std=0.01)
nn.init.normal_(self.embed_item_MLP.weight, std=0.01)
for m in self.MLP_layers:
if isinstance(m, nn.Linear):
nn.init.xavier_uniform_(m.weight)
nn.init.kaiming_uniform_(self.predict_layer.weight,
a=1, nonlinearity='sigmoid')
for m in self.modules():
if isinstance(m, nn.Linear) and m.bias is not None:
m.bias.data.zero_()
else:
# embedding layers
self.embed_user_GMF.weight.data.copy_(
self.GMF_model.embed_user_GMF.weight)
self.embed_item_GMF.weight.data.copy_(
self.GMF_model.embed_item_GMF.weight)
self.embed_user_MLP.weight.data.copy_(
self.MLP_model.embed_user_MLP.weight)
self.embed_item_MLP.weight.data.copy_(
self.MLP_model.embed_item_MLP.weight)
# mlp layers
for (m1, m2) in zip(
self.MLP_layers, self.MLP_model.MLP_layers):
if isinstance(m1, nn.Linear) and isinstance(m2, nn.Linear):
m1.weight.data.copy_(m2.weight)
m1.bias.data.copy_(m2.bias)
# predict layers
predict_weight = torch.cat([
self.GMF_model.predict_layer.weight,
self.MLP_model.predict_layer.weight], dim=1)
precit_bias = self.GMF_model.predict_layer.bias + \
self.MLP_model.predict_layer.bias
self.predict_layer.weight.data.copy_(0.5 * predict_weight)
self.predict_layer.bias.data.copy_(0.5 * precit_bias)
def forward(self, user, item):
if not self.model == 'MLP':
embed_user_GMF = self.embed_user_GMF(user)
embed_item_GMF = self.embed_item_GMF(item)
output_GMF = embed_user_GMF * embed_item_GMF
if not self.model == 'GMF':
embed_user_MLP = self.embed_user_MLP(user)
embed_item_MLP = self.embed_item_MLP(item)
interaction = torch.cat((embed_user_MLP, embed_item_MLP), -1)
output_MLP = self.MLP_layers(interaction)
if self.model == 'GMF':
concat = output_GMF
elif self.model == 'MLP':
concat = output_MLP
else:
concat = torch.cat((output_GMF, output_MLP), -1)
prediction = torch.sigmoid(self.predict_layer(concat))
return prediction.view(-1)
Training: take GMF as an example, others are the same
GMF_model = GMF(user_num = user_num,item_num = item_num,factor_num = 8)
lr = 0.001 epochs = 10 topK = 10 evaluation_threads = 1 Adam_optimizer = torch.optim.Adam(GMF_model.parameters(), lr )
loss_list = []
s = time.time()
for epoch in range(epochs):
for i,data in enumerate(data_train):
user_data = data[:,0].reshape(1,-1).long()#Because we put together the training set before,
item_data = data[:,1].reshape(1,-1).long()#So we need to open it here
label = data[:,2]
Adam_optimizer.zero_grad()
predict = GMF_model(user_data,item_data)
loss_func = nn.BCELoss()
#loss_func = nn.MSELoss()
loss = loss_func(predict,label)
loss.backward()
Adam_optimizer.step()
loss_list.append(loss)
(hits, ndcgs) = evaluate_model(GMF_model, testRatings, testNegatives, topK, evaluation_threads)
hr, ndcg = np.array(hits).mean(), np.array(ndcgs).mean()
HR.append(hr)
NDCG.append(ndcg)
print(loss_list[-1])
print(HR)
print(NDCG)
e = time.time()
print(e-s)
Save model:
torch.save(GMF_model,'GMF_model.pkl')
Take model
GMF_model = torch.load("GMF_model.pkl")
Save data:
torch.save(HR,'P_GMF_8_hr')
Fetch data:
data = torch.load("P_GMF_8_hr")
Thesis source address: Mr. He Nanan