AcWing 785. Quick sort

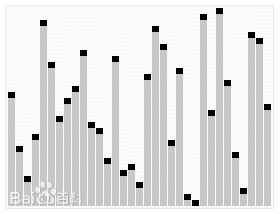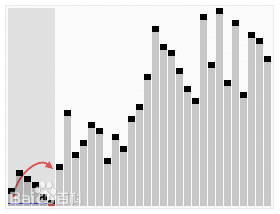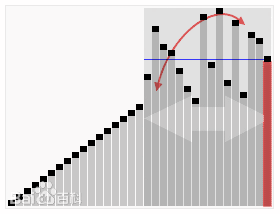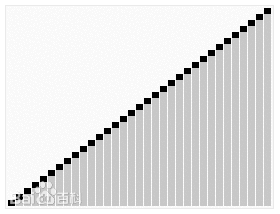
Quick sort is essentially a divide and conquer method

1. Decompose into subproblems
2. Recursive processing subproblem
3. Merge subproblem
   

#include<iostream>
using namespace std;

const int N = 1e6 + 10;

int n;
int q[N];

void quick_sort(int q[], int l, int r)
{
	//In the case of recursive boundary, the subproblem cannot be decomposed at this time
    if(l >= r) return;
	
	//Decompose into subproblems
    int x = q[(l + r) >> 1], i = l - 1, j = r + 1;
    while(i < j)
    {
        do i ++ ; while(q[i] < x);
        do j -- ; while(q[j] > x);
        if(i < j) swap(q[i], q[j]); 
    }
	
	//Recursive processing subproblem
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);
}

int main()
{
    scanf("%d", &n);
    for(int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    quick_sort(q, 0, n - 1);

    for(int i = 0; i < n; i ++ ) printf("%d ", q[i]);

    return 0;
}

AcWing 786. Number k

A form of divide and conquer
Each time you just need to judge whether K is in the left or right interval, always recursively find the interval where k is located, and the other interval is rounded off
When there is only one number left, there will be only one number in array [k]. The answer is to return the value of array [k]

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, k;
int q[N];

int quick_sort(int l, int r, int k)
{
    if(l == r) return q[l];

    int x = q[l], i = l - 1, j = r + 1;
    while(i < j)
    {
        while(q[ ++ i] < x);
        while(q[ -- j] > x);
        if(i < j) swap(q[i], q[j]);
    }
	
	//Judge the interval where k is located, and sl represents the length of the left interval
    int sl = j - l + 1;
    
	//k in left interval
    if(k <= sl) return quick_sort(l, j, k);		
    //k is in the right interval, and k - sl represents the position of k in the right interval
    else return quick_sort(j + 1, r, k - sl);	
}

int main()
{
    cin >> n >> k;
    for(int i = 0; i < n; i ++ ) cin >> q[i];
    cout << quick_sort(0, n - 1, k) << endl;

    return 0;
}

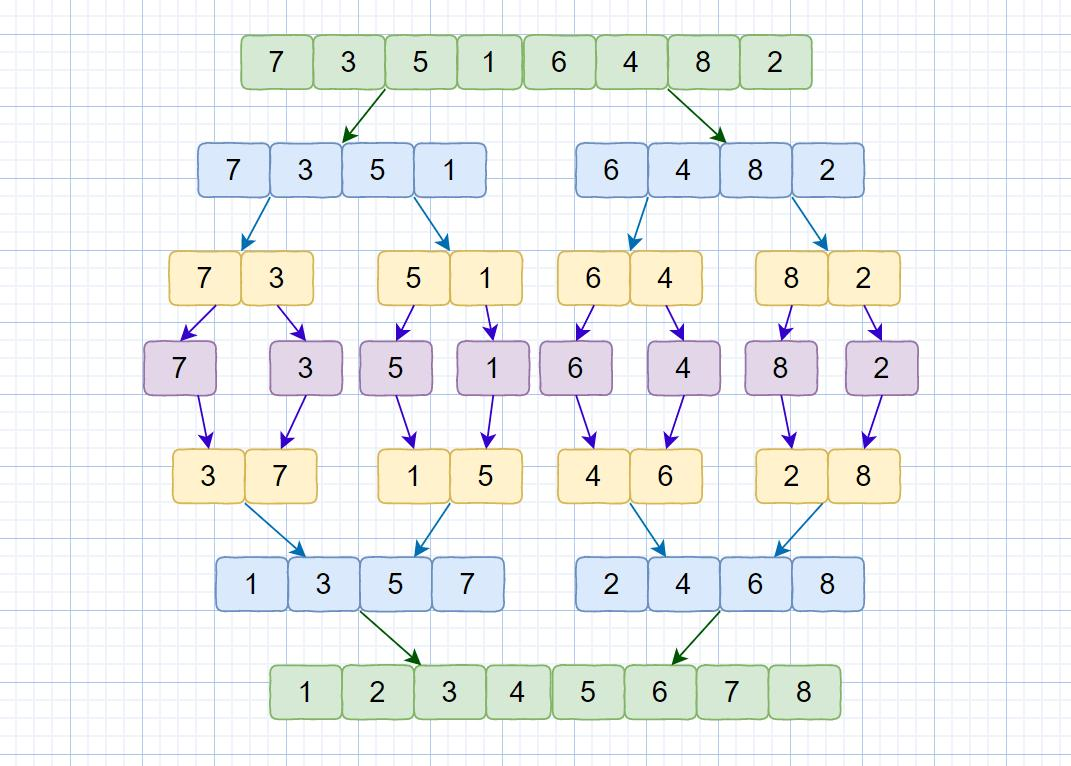
AcWing 787. Merge sort

Typical of divide and conquer

1. Decompose into subproblems
2. Recursive processing subproblem
3. Merge subproblem
   

#include<iostream>
using namespace std;

const int N = 1e6 + 10;
int n;
int q[N], tmp[N];		//tmp as auxiliary array

void merge_sort(int q[], int l, int r)
{
	//The subproblem can no longer be decomposed
	if(l >= r) return;

	//Decomposition subproblem
	int mid = l + r >> 1;
	merge_sort(q, l, mid);
	merge_sort(q, mid + 1, r);
	
	//Merge subproblem
	int k = 0, i = l, j = mid + 1;
	
    while(i <= mid && j <= r)
	{
		if(q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
		else tmp[k ++ ] = q[j ++ ];
	}

	while(i <= mid) tmp[k ++ ] = q[i ++ ];
	while(j <= r) tmp[k ++ ] = q[j ++ ];

	for(i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];
}

int main()
{
	scanf("%d", &n);
	for(int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

	merge_sort(q, 0, n - 1);
	for(int i = 0; i < n; i ++ ) printf("%d ", q[i]);

	return 0;
}

AcWing 788. Number of pairs in reverse order

#include<iostream>
using namespace std;

typedef long long LL;

const int N = 1e6 + 10;

int n;
int q[N], tmp[N];

LL merge_sort(int l, int r)
{
    if(l >= r) return 0;

    int mid = l + r >> 1;
    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
        if(q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];
        else
        {
            tmp[k ++ ] = q[j ++ ];
            res += mid - i + 1;
        }

    while(i <= mid) tmp[k ++ ] = q[i ++ ];
    while(j <= r) tmp[k ++ ] = q[j ++ ];

    for(int i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];

    return res;
}

int main()
{
    cin >> n;

    for(int i = 0; i < n; i ++ ) cin >> q[i];

    cout << merge_sort(0, n - 1) << endl;

    return 0;
}

AcWing 789. Range of numbers

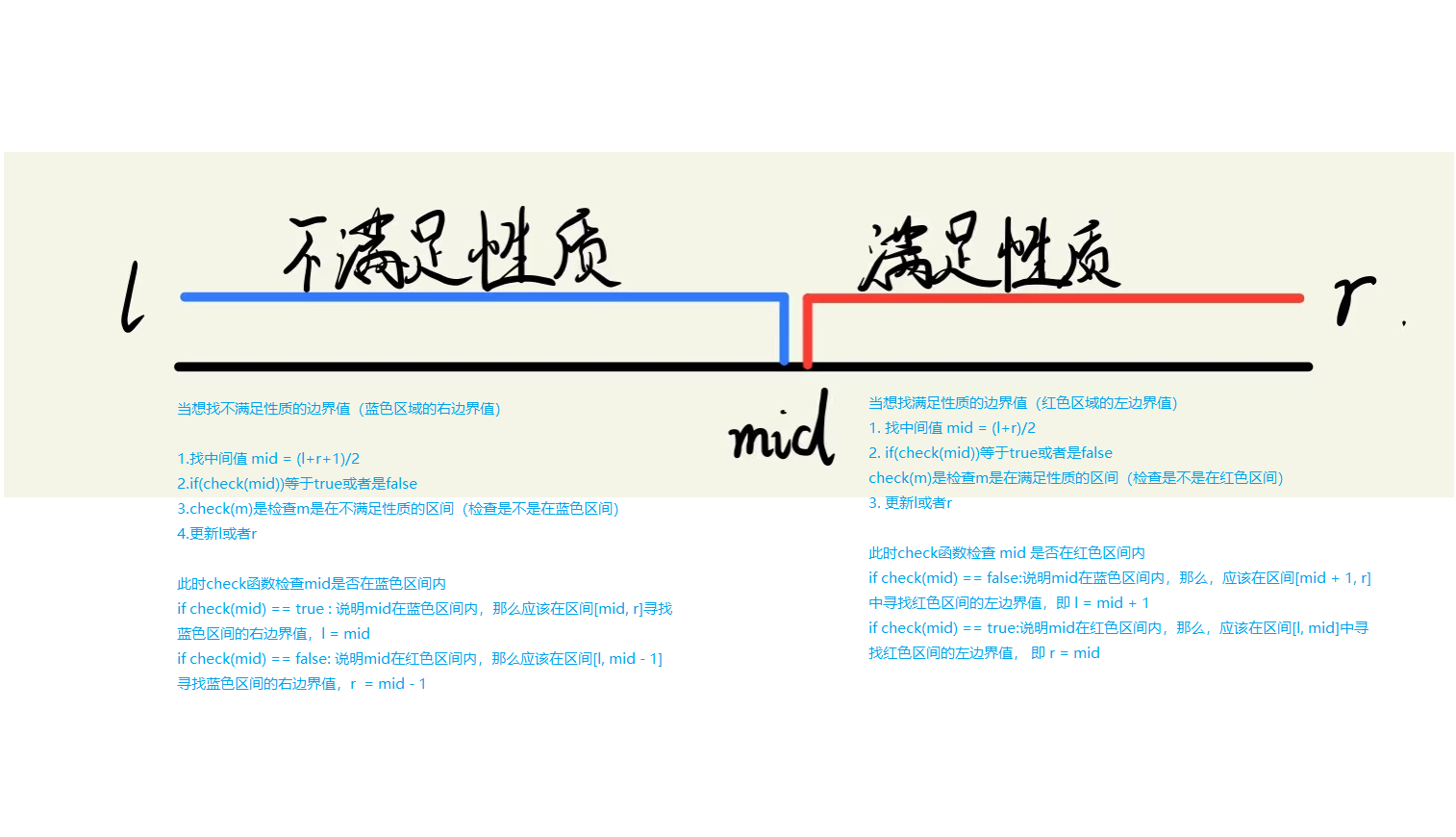
A typical dichotomy problem

When you want to find a boundary value that does not satisfy the property (the right boundary value of the blue area)

1. Find the middle value mid = (l+r+1)/2
2. if(check(mid)) is equal to true or false
3. check(m) is to check whether M is in the interval that does not satisfy the property (check whether it is in the blue interval)
4. Update l or r

At this time, the check function checks whether the mid is within the blue range
if check(mid)== true: indicates that mid is in the blue interval, then the right boundary value of the blue interval should be found in the interval [mid, r], l = mid
if check(mid)== false: indicates that mid is in the red range, then the right boundary value of the blue range should be found in the range [l, mid - 1], r = mid - 1

When you want to find the five boundary values (the difference boundary value in the red region) that are fully defined in quality

1. Find intermediate value mid = (l+r)/2
2. if(check(mid)) is equal to true or false
3. check(m) is to check whether M is in the interval satisfying the property (check whether it is in the red interval)
4. Update l or r

At this time, the check function checks whether the mid is within the red range
if check(mid)== false: indicates that mid is in the blue range, then the left boundary value of the red range should be found in the range [mid + 1, r], i.e. l= mid + 1
if check(mid)== true: indicates that mid is within the red interval, then the left bound value of the red interval should be found in the interval [l, mid], that is, r = mid

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0; i < n; i ++ ) scanf("%d", &q[i]);

    while(m -- )
    {
        int x;
        scanf("%d", &x);

        int l = 0, r = n - 1;
        
        //Check left boundary
        while(l < r)
        {
            int mid = l + r >> 1;
            if(q[mid] >= x) r = mid;
            else l = mid + 1;
        }
        if(q[l] != x) cout << "-1 -1" << endl;
        else
        {
            cout << l << " ";

            int l = 0, r = n - 1;
            //Check right boundary
            while(l < r)
            {
                int mid = l + r + 1 >> 1;
                if(q[mid] <= x) l = mid;
                else r = mid - 1;
            }
            cout << r << endl;
        }
    }
    return 0;
}

AcWing 790. The cubic root of a number

Dichotomy to deal with problems

#include<iostream>
using namespace std;

int main()
{
	double x;
	cin >> x;

	double l = -10000, r = 10000;
	while(r - l > 1e-8)
	{
		double mid = (l + r) / 2;
		if(mid * mid * mid >= x) r = mid;
		else l = mid;
	}
	printf("%lf", l);
	return 0;
}

AcWing 791. High precision addition

Simulate the following vertical form for addition, and use a variable carry for carry operation,

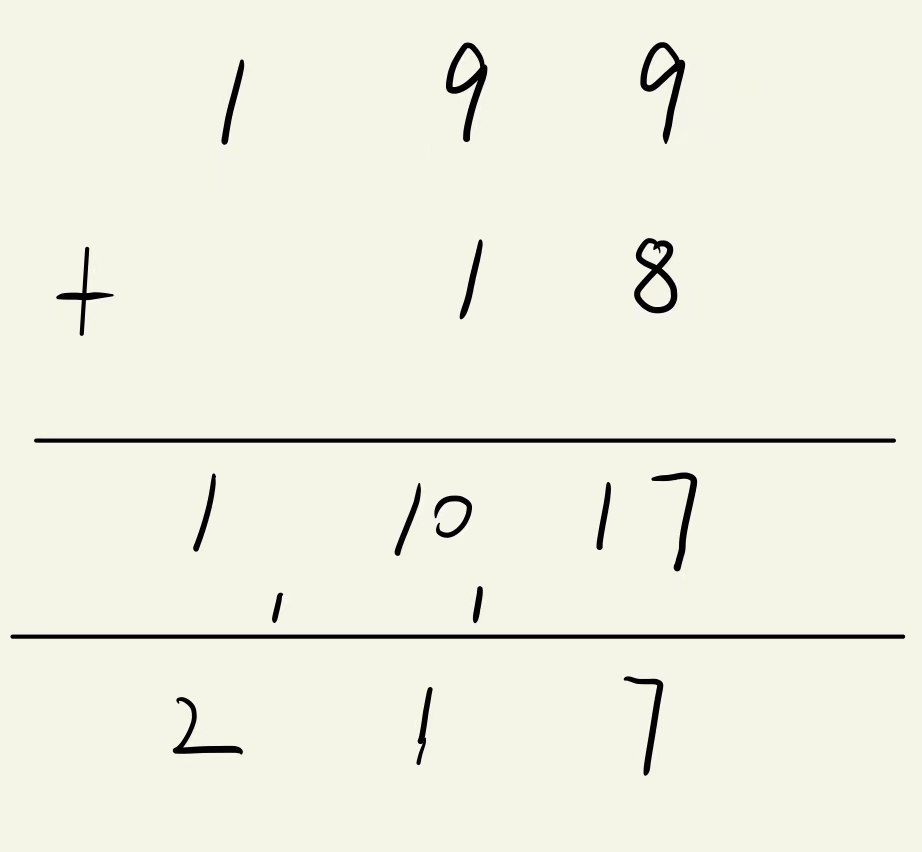
#include<iostream>
#include<vector>
using namespace std;

vector<int> add(vector<int> &A, vector<int> &B)
{
	vector<int> C;

	int t;
	for(int i = 0; i < A.size() || i < B.size(); i ++ )
	{
		if(i < A.size()) t += A[i];
		if(i < B.size()) t += B[i];
		C.push_back(t % 10);
		t /= 10;	
	}
	if(t) C.push_back(1);
	return C;
}

int main()
{
	string a, b;
	vector<int> A, B;

	cin >> a >> b;
	for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
	for(int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

	auto C = add(A, B);
	for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);

	return 0;
}

AcWing 792. High precision subtraction

#include<iostream>
#include<vector>
using namespace std;

bool cmp(vector<int> &A, vector<int> &B)
{
	if(A.size() != B.size()) return A.size() > B.size();

	for(int i = A.size() - 1; i >= 0; i -- )
		if(A[i] != B[i])
			return A[i] > B[i];

	return true;
}

vector<int> sub(vector<int> &A, vector<int> &B)
{
	vector<int> C;
	for(int i = 0, t = 0; i < A.size(); i ++ )
	{
		t = A[i] - t;
		if(i < B.size()) t -= B[i];
		C.push_back((t + 10) % 10);
		if(t < 0) t = 1;
		else t = 0;
	}
	while(C.size() > 1 && C.back() == 0) C.pop_back();
	return C; 
}

int main()
{
	string a, b;
	vector<int> A, B;
	
	cin >> a >> b;
	
	for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
	for(int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

	if(cmp(A, B))
	{
		auto C = sub(A, B);
		for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
	}
	else
	{
		auto C = sub(B, A);
		printf("-");
		for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
	}
	
	return 0;
}

AcWing 793. High precision multiplication

#include<iostream>
#include<vector>

using namespace std;

vector<int> mul(vector<int> &A, vector<int> &B)
{
	vector<int> C(A.size() + B.size());

	for(int i = 0; i < A.size(); i ++ )
		for(int j = 0; j < B.size(); j ++ )
			C[i + j] += A[i] * B[j];
	
	for(int i = 0, t = 0; i < C.size() || t; i ++ )
	{
		t += C[i];
		if(i >= C.size()) C.push_back(t % 10);
		else C[i] = t % 10;

		t /= 10;
	}
	while(C.size() > 1 && C.back() == 0) C.pop_back();

	return C;
}

int main()
{
	string a, b;
	cin >> a >> b;

	vector<int> A, B;

	for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');
	for(int i = b.size() - 1; i >= 0; i -- ) B.push_back(b[i] - '0');

	auto C = mul(A, B);

	for(int i = C.size() - 1; i >= 0; i -- ) cout  << C[i];
	puts("");

	return 0;
}

AcWing 794. High precision Division

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

vector<int> div(vector<int> &A, int b, int &r)
{
	vector<int> C;
	r = 0;
	for(int i = A.size() - 1; i >= 0; i -- )
	{
		r = r * 10 + A[i];
		C.push_back(r / b);
		r = r % b;
	}
	reverse(C.begin(), C.end());
	while(C.size() > 1 && C.back() == 0) C.pop_back();
	return C;
}

int main()
{
	string a;
	int b;

	cin >> a >> b;
	vector<int> A;
	for(int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

	int r;
	auto C = div(A, b, r);

	for(int i = C.size() - 1; i >= 0; i -- ) printf("%d", C[i]);
	cout << endl << r << endl;

	return 0;
}

AcWing 795. Prefix and

Original array: a[1], a[2], a[3], a[4], a[5],..., a[n]
Prefix and: S[i] = a[1] + a[2] + a[3] +... + a[i]
Function: you can quickly find the sum of a continuous interval in the array
Usage: find the sum of arrays a [l], a [L + 1], a [L + 2],..., a [R], i.e. S[r] - S[l - 1]

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int a[N], s[N];

int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

	for(int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];

	while(m -- )
	{
		int l, r;
		scanf("%d%d", &l, &r);
		printf("%d\n", s[r] - s[l - 1]);
	}
    
	return 0;
}

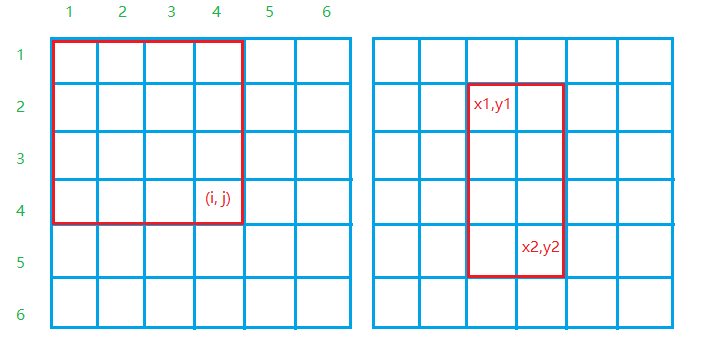
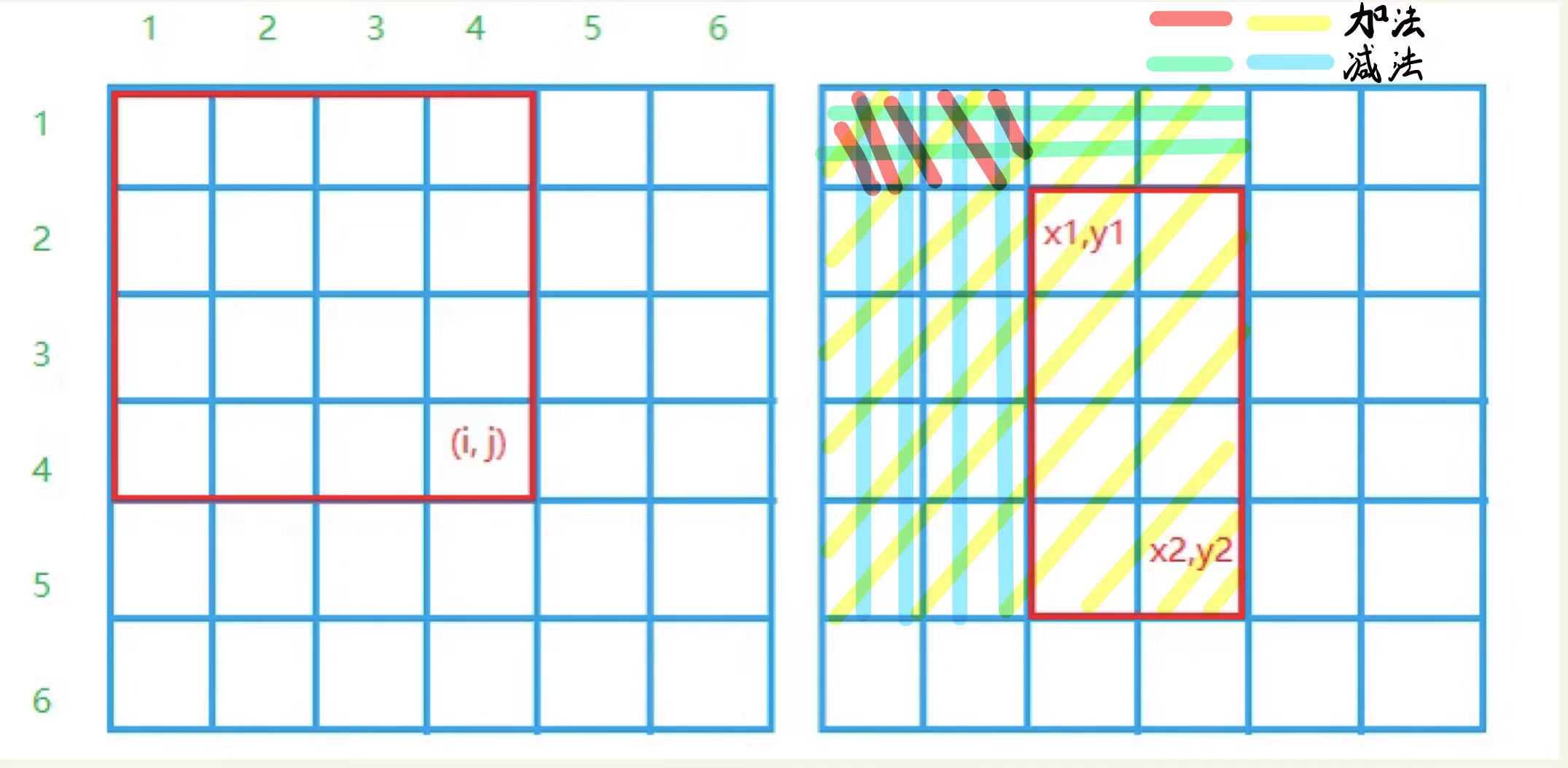
AcWing 796. Sum of submatrixes

S[i, j] represents the sum of the elements of the matrix from a[1, 1] to a[i, j]
S [ i , j ] = S [ i , j − 1 ] + S [ i − 1 , j ] − S [ i − 1 , j − 1 ] + a [ i , j ] S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j] S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]

(x1,y1) to (x2, y2) are the calculation formulas of this submatrix
S [ x 2 , y 2 ] − S [ x 1 − 1 , y 2 ] − S [ x 2 , y 1 − 1 ] + S [ x 1 − 1 , y 1 − 1 ] S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1] S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]

#include<iostream>
using namespace std;

const int N = 1010;

int m, n, q;
int a[N][N], s[N][N];

int main()
{
	scanf("%d%d%d", &n, &m, &q);
	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			scanf("%d", &a[i][j]);

	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];

	while(q -- )
	{
		int x1, y1, x2, y2;
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
	}

	return 0;
}

AcWing 797. Differential

First, give an original array a: a [ 1 ] , a [ 2 ] , a [ 3 ] , , , , , , a [ n ] ; a[1], a[2], a[3],,,,,, a[n]; a[1],a[2],a[3],,,,,,a[n];
Then we construct an array b: b [ 1 ] , b [ 2 ] , b [ 3 ] , , , , , , b [ i ] ; b[1] ,b[2] , b[3],,,,,, b[i]; b[1],b[2],b[3],,,,,,b[i];
bring a [ i ] = b [ 1 ] + b [ 2 ] + b [ 3 ] + , , , , , , + b [ i ] a[i] = b[1] + b[2 ]+ b[3] +,,,,,, + b[i] a[i]=b[1]+b[2]+b[3]+,,,,,,+b[i]

a [ 0 ] = 0 ; a[0 ]= 0; a[0]=0;
b [ 1 ] = a [ 1 ] − a [ 0 ] ; b[1] = a[1] - a[0]; b[1]=a[1]−a[0];
b [ 2 ] = a [ 2 ] − a [ 1 ] ; b[2] = a[2] - a[1]; b[2]=a[2]−a[1];
b [ 3 ] = a [ 3 ] − a [ 2 ] ; b[3] =a [3] - a[2]; b[3]=a[3]−a[2];
...
b [ n ] = a [ n ] − a [ n − 1 ] ; b[n] = a[n] - a[n-1]; b[n]=a[n]−a[n−1];
From the formula, we can know that array A is the prefix and array of array b, and conversely, array b is the differential array of array a

Application scenario:
Given the interval [l, r], let's add c to each number in the interval [l, r] in the array a, that is
a [ l ] + c , a [ l + 1 ] + c , a [ l + 2 ] + c , . . . , a [ r ] + c ; a[l] + c , a[l+1] + c , a[l+2] + c ,... , a[r] + c; a[l]+c,a[l+1]+c,a[l+2]+c,...,a[r]+c;
If you simply use the for loop to add, the time complexity of m times plus c is O ( n ∗ m ) O(n * m) O(n∗m)

At this time, to reduce the time complexity, you can use the differential array
A array is the prefix and array of b array. For example, the modification of b[i] of b array will affect every number from a[i] to the next in a array.
First, let the difference in the b array b [ l ] + c b[l] + c B [l] + C, a array becomes a [ l ] + c , a [ l + 1 ] + c , . . . , a [ n ] + c a[l] + c ,a[l+1] + c,..., a[n] + c a[l]+c,a[l+1]+c,...,a[n]+c;

Then, in order to avoid affecting the value after the coordinate r in the array, b [ r + 1 ] − c b[r+1] - c b[r+1] − c, a array becomes a [ r + 1 ] − c , a [ r + 2 ] − c , . . . , a [ n ] − c a[r+1] - c,a[r+2] - c,...,a[n] - c a[r+1]−c,a[r+2]−c,...,a[n]−c;

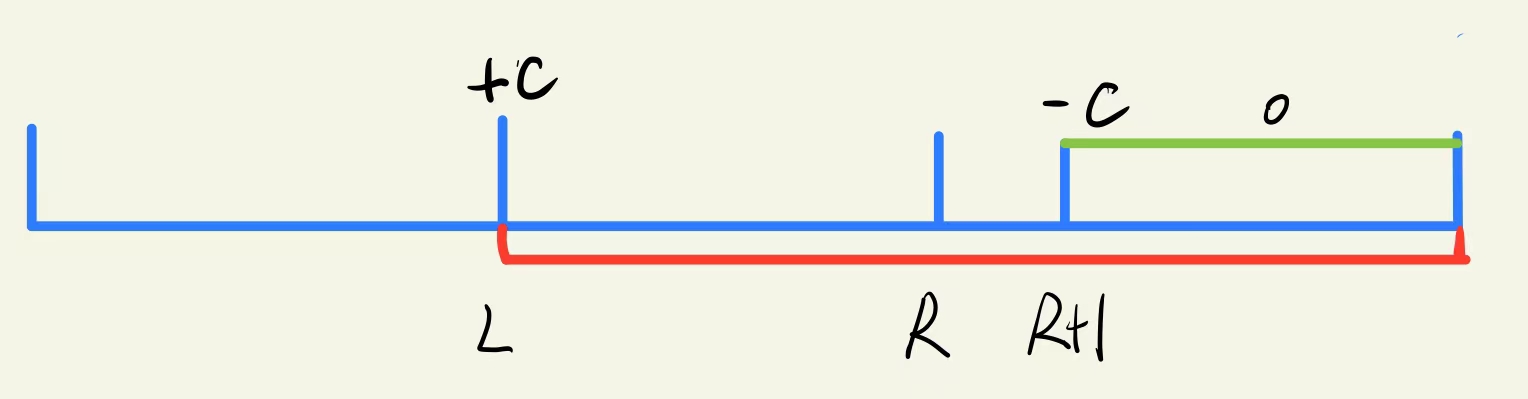
Therefore, adding a number c to the [l, r] interval of the one-dimensional difference pair a array only needs to make a difference for its difference group b b [ l ] + = c b[l] += c b[l]+=c, b [ r + 1 ] − = c b[r + 1] -= c b[r+1] − = c, with time complexity of O ( 1 ) O(1) The overall time complexity of O(1), m operations is from O ( n ∗ m ) O(n*m) O(n * m) is reduced to O ( m ) O(m) O(m)

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
	b[l] += c;
	b[r + 1] -= c;
}

int main()
{
	scanf("%d%d", &n, &m);

	for(int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
	for(int i = 1; i <= n; i ++ ) insert(i, i, a[i]);

	while(m -- )
	{
		int l, r, c;
		scanf("%d%d%d", &l, &r, &c);
		insert(l, r, c);
	}

	for(int i = 1; i <= n; i ++ ) b[i] += b[i - 1];
	for(int i = 1; i <= n; i ++ ) printf("%d ", b[i]);
	return 0;
}

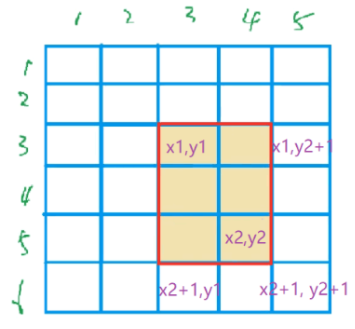
AcWing 798. Difference matrix

It is similar to the process of one-dimensional prefix and extending to two-dimensional prefix and
One dimensional difference extends to two-dimensional difference
Core operations:
b [ x 1 ] [ y 1 ] + = c ; b[x1][y1] += c; b[x1][y1]+=c;
b [ x 2 + 1 ] [ y 1 ] − = c ; b[x2 + 1][y1] -= c; b[x2+1][y1]−=c;
b [ x 1 ] [ y 2 + 1 ] − = c ; b[x1][y2 + 1] -= c; b[x1][y2+1]−=c;
b [ x 2 + 1 ] [ y 2 + 1 ] + = c ; b[x2 + 1][y2 + 1] += c; b[x2+1][y2+1]+=c;

#include<iostream>
using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], b[N][N];

void insert(int x1, int y1, int x2, int y2, int c)
{
	b[x1][y1] += c;
	b[x2 + 1][y1] -= c;
	b[x1][y2 + 1] -= c;
	b[x2 + 1][y2 + 1] += c;
}

int main()
{
	scanf("%d%d%d", &n, &m, &q);

	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			scanf("%d", &a[i][j]);

	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			insert(i, j, i, j, a[i][j]);
	
	while(q -- )
	{
		int x1, y1, x2, y2, c;
		cin >> x1 >> y1 >> x2 >> y2 >> c;
		insert(x1, y1, x2, y2, c);
	}

	for(int i = 1; i <= n; i ++ )
		for(int j = 1; j <= m; j ++ )
			b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
	
	for(int i = 1; i <= n; i ++ )
	{
		for(int j = 1; j <= m; j ++ )
			printf("%d ", b[i][j]);
		puts("");
	}
	return 0;
}

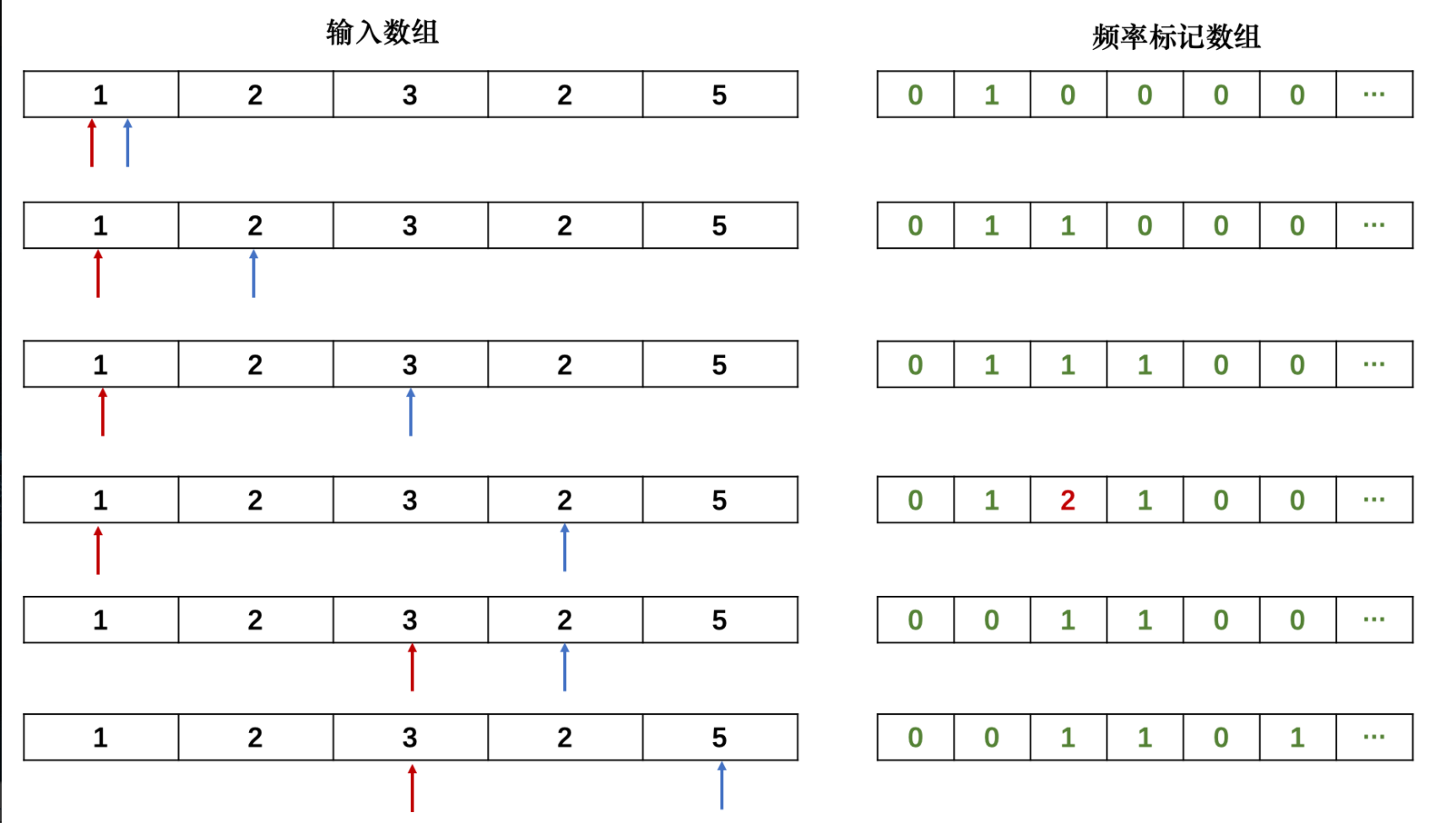
AcWing 799. Longest continuous unrepeated subsequence

Double pointer algorithm.
Use an array s to maintain the number of numbers in the currently found interval [i, j].
If there is a duplicate number, the pointer i moves back one bit, and the number of occurrences of this number in the hash table is reduced by one until there is no duplicate character. A while loop is used
If the array is not repeated, the pointer j moves back one bit, and the number of occurrences of the corresponding number in s increases by one
In this process, res is used to record the maximum length of the subsequence.

#include<iostream>
using namespace std;

const int N = 1e6 + 10;

int a[N], s[N];
int n;

int main()
{
	cin >> n;
	for(int i = 0; i < n; i ++ ) cin >> a[i];

	int res = 0;
	for(int i = 0, j = 0; i < n; i ++ )
	{
		s[a[i]] ++ ;
		while(s[a[i]] > 1)
		{
			s[a[j]] -- ;
			j ++ ;
		}
		res = max(res, i - j + 1);
	}
	cout << res << endl;

	return 0;
}

AcWing 800. Destination and destination of array elements

i start from 0 and traverse from front to back
J starts from m - 1 and traverses backward and forward, and the j pointer does not fall back

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m, x;
int a[N], b[N];

int main()
{
	scanf("%d%d%d", &n, &m, &x);
	
	for(int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
	for(int i = 0; i < m; i ++ ) scanf("%d", &b[i]);

	for(int i = 0, j = m - 1; i < n; i ++ )
	{
		while(j > 0 && a[i] + b[j] > x) j -- ;
		if(j >= 0 && a[i] + b[j] == x)
			cout << i << " " << j << endl;
	}
	return 0;
}

AcWing 2816. Judgment subsequence

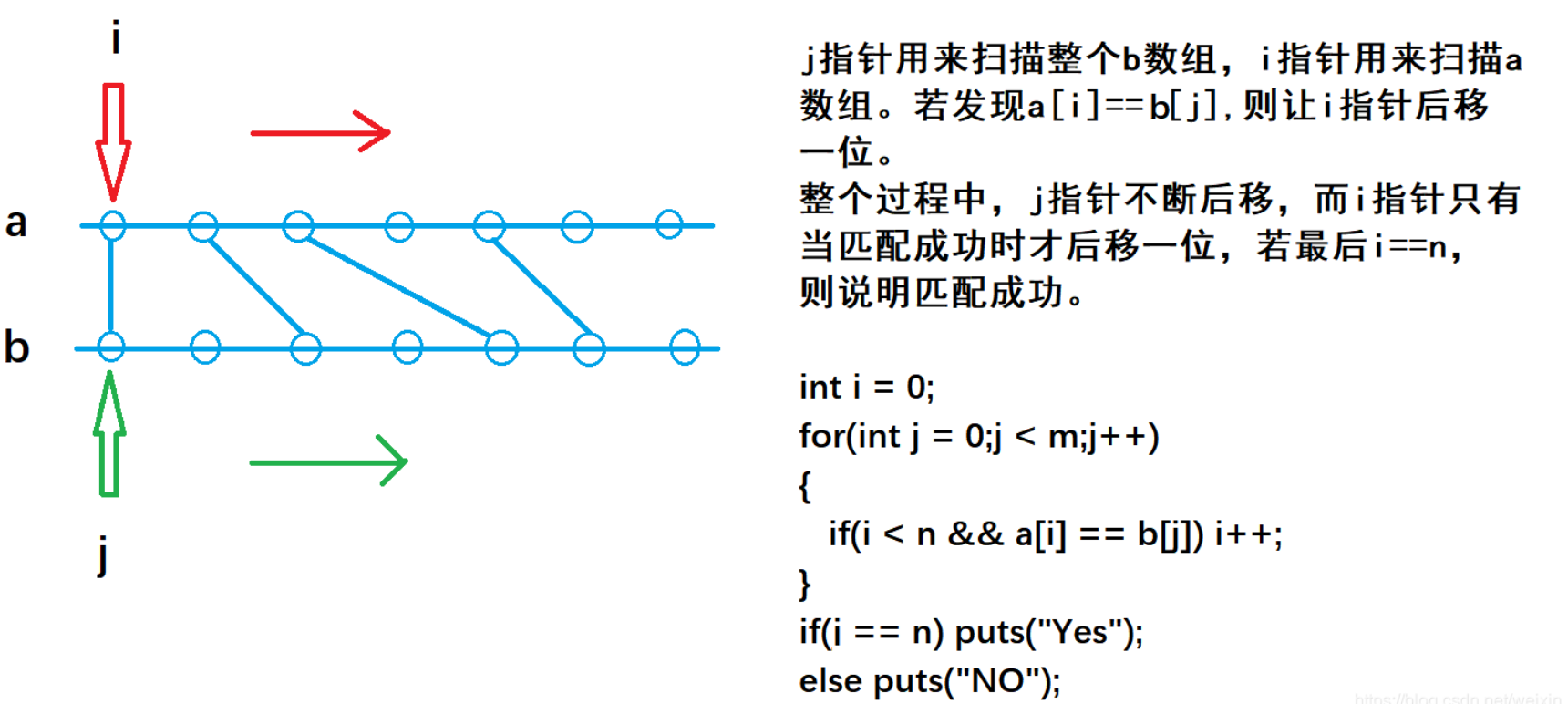
1. The j pointer is used to scan the entire b array, and the I pointer is used to scan the a array. If a[i]==b[j], move the I pointer back one bit.
2. In the whole process, the j pointer moves back continuously, while the i pointer moves back one bit only when the matching is successful. If i==n, the matching is successful.

#include<iostream>
using namespace std;

const int N = 1e5 + 10;

int n, m;
int a[N], b[N];

int main()
{
	cin >> n >> m;

	for(int i = 0; i < n; i ++ ) cin >> a[i];
	for(int i = 0; i < m; i ++ ) cin >> b[i];

	int j = 0;
	for(int i = 0; i < m; i ++ )
		if(b[i] == a[j])
			j ++ ;
	
	if(j == n) cout << "Yes" << endl;
	else cout << "No" << endl;

	return 0;
}

AcWing 801. Number of 1 in binary

Bitwise sum operation

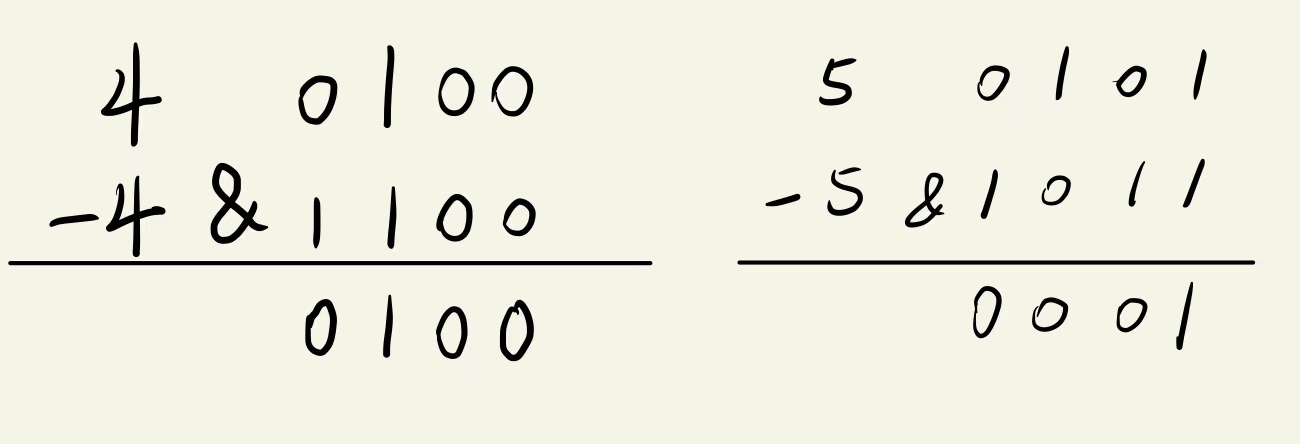
#include<iostream>
using namespace std;

int lowBit(int x)
{
	return x & -x;
}

int main()
{
	int n;
	cin >> n;
	while(n -- )
	{
		int x;
		cin >> x;
		
		int res = 0;
		while(x) 
		{
			x -= lowBit(x);
			res ++ ;
		}

		cout << res << " ";
	}
	return 0;
}

AcWing 802. Interval and

Problem solution

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

typedef pair<int, int> PII;
const int N = 3e5 + 10;

int n, m;
int a[N], s[N];

vector<int> all;
vector<PII> add, query;

int find(int x)
{
    int l = 0, r = all.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(all[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main()
{
    cin >> n >> m;

    for(int i = 0; i < n; i ++ )
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        all.push_back(x);
    }

    for(int i = 0; i < m; i ++ )
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});

        all.push_back(l);
        all.push_back(r);
    }

    sort(all.begin(), all.end());
    all.erase(unique(all.begin(), all.end()), all.end());

    for(auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }

    for(int i = 1; i <= all.size(); i ++ ) s[i] = s[i - 1] + a[i];

    for(auto item : query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }

    return 0;
}

AcWing 803. Interval merging

The way of thinking is similar to greed

1. First, sort each interval by the left endpoint
2. Traverse each interval
   If the starting point of the second interval is less than the end point of the first interval, there is an intersection. Update the end point of the first interval to the end point of the second interval
   If there is no intersection, the previously updated interval is stored
   

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;

typedef pair<int, int> PII;

int n;
vector<PII> seg;

void merge(vector<PII> &Seg)
{
    vector<PII> res;
    int st = -2e9, ed = -2e9;
    sort(Seg.begin(), Seg.end());
    for(auto seg : Seg)
    {
        if(ed < seg.first)
        {
            if(ed != -2e9) res.push_back({st, ed});
            st = seg.first;
            ed = seg.second;
        }
        else ed = max(ed, seg.second);
    }
    if(st != -2e9) res.push_back({st, ed});
    Seg = res;  
}

int main()
{
    cin >> n;
    for(int i = 0; i < n; i ++ )
    {
        int l, r;
        cin >> l >> r;
        seg.push_back({l, r});
    }
    merge(seg);
    cout << seg.size() << endl;
    return 0;
}