1. Introduction

Common operations of data structure: insert, delete and find. That is, a data structure should generally have the functions of inserting, deleting and searching. For example, for the stack, the operations supported by the stack are inserting and deleting from the top of the stack. You cannot operate at the bottom of the stack or at any position of the stack.

Secondly, after knowing the supported operations, we also need to clearly know the time complexity of each operation and the importance of time complexity, which we have introduced earlier. If we don't know the time complexity of each operation in a data structure, if our solution uses the data structure, we can't calculate the overall time complexity of the solution

After understanding the common operations and time complexity, we also need to understand the implementation of this data structure. For example, we know that there is a List data structure in Python, which is essentially an array whose size can be adjusted dynamically. But we know that when we apply for memory from the computer, we usually can only apply for occupying a continuous piece of memory, which is obviously contrary to dynamic resizing. Therefore, the implementation of dynamic array is not as simple as we take it for granted. We will discuss this problem in detail in the later explanation.         

Finally, we need to know how to use the data structure, that is, whether there is a definition of the data structure in the language we are familiar with, and how its interface should be used. It doesn't matter if you are not familiar with it at present. In the follow-up training, we need to use a lot of various data structures to improve our sensitivity and proficiency in data structures.

2. Introduction to data structure

2.1 linear data structure

2.1.1 array

General support required:

• push_back - insert a new element at the end of the array - 
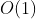
• pop_back - deletes the last element in the array -
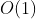
• size - return array length -
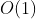
• Index - returns the element with index i in the array -

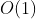
These operations are generally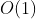Complete within the required time.

2.1.2 stack

The badminton cylinder can only operate on the top (tail), last in first out, and generally needs to support:

• push - put an element on the stack - 
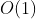
• pop - remove an element from the stack - 
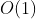
• Top - get stack top element - 
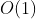
• Size - returns the stack size - 

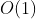
Search is generally not supported. These operations are generally performed in the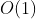Complete within the required time.

2.2.3 queue

Like the stack, they are linear tables with restricted operations. They can only insert the tail and delete the head

• push - put an element to the end of the queue - 
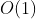
• pop - delete an element from the head of the team - 
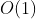
• front - get team leader element - 
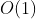
• Size - returns the size of the queue - 

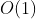
These operations are generally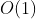Complete within the required time.

2.2.4 double ended queue

Both ends of the queue can be inserted and deleted. If only one end is used, the two end queue will become a stack; If one end is inserted and one end is deleted, it will become an ordinary queue.

2.2.5 linked list

A train with many cars,

• Locomotive - chain header node
• From each car, you can reach the next car, not the front car
• Each carriage can store goods (data)

operation

• Insert - first point the hook of the previous car to the new car, and then point the hook of the new car to the next car - O(1)
• Delete - direct the hook of the previous carriage of the carriage to be deleted to the next carriage - O(1)
• Find the K-th node - search from the beginning to the next node. Try to avoid random search - O(n)
• Find previous node - find from scratch node by node - O(n)

2.2 other data structures

2.2.1 dictionary

Record the occurrence of an element before, and record the corresponding attributes of the element

classification

• Unordered Dictionary - based on hash algorithm, the storage and mapping of elements can be realized in O(1), but the relative size order cannot be preserved
• Balanced tree can be used in C + +

2.2.2 tree

When a node has multiple successor nodes, but each node has only one precursor node, it is a tree

3. Examples

3.1 implementation of dynamic array

Dynamic array: an array whose length can be changed dynamically. C + + Vector and python list are all dynamic arrays.

• Meet the dynamic change of length
• The random search efficiency of the array is not lost

Operation requirements of dynamic array

• push_back - inserts a new element at the end of the array
• pop_back - deletes the last element in the array
• size - returns the length of the array
• Index - returns the element with index i in the array

Static array: an array whose capacity cannot be changed at any time. Allocating a whole block of continuous memory can faster address and access, and meet the characteristics of random search of arrays

Operation and implementation of dynamic array

• push_back - judge whether the current array size is full. If it is full, apply for an array with twice the capacity, copy all contents and insert a new number
• pop_back - delete the last element in the array, array size - 1
• size - returns the current number of elements
• Index - returns the array element with index i directly

Let the array length of the final application be n, and the total size of the application space be n + n/2 + n/4 + 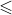  2n

The time complexity is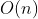

class LCArray {

private:
 int curSize;
 int maxSize;
 int* array;

public:     
    LCArray() {                             
        curSize = 0;    
        maxSize = 1;
        array = new int[1];  //  Allocate memory space to pointers, that is, allocate memory space to arrays
    }            //  initialization
    
    void push_back(int n) {
        if (curSize == maxSize)
        {
            maxSize *= 2;
            int* tmp = array;
            array = new int[maxSize];  // array points to a new memory space
            for (int i = 0; i < curSize; i++)
            {
                array[i] = tmp[i];
            }
            delete [] tmp;
        }
        
        array[curSize] = n;   // The index starts at 0 and gives the number to be inserted to the end of the array
        curSize += 1;        // Current array size + 1
    }
    
    void pop_back() {
        curSize -= 1;
    }
    
    int size() {
        return curSize;
    }
    
    int index(int idx) {
        return array[idx];
    }
};

/**
 * Your LCArray object will be instantiated and called as such:
 * LCArray* obj = new LCArray();
 * obj->push_back(n);
 * obj->pop_back();
 * int param_3 = obj->size();
 * int param_4 = obj->index(idx);
 */

3.2 implementing stack with queue

(Leecode 225) please use only two queues to implement a last in first out (LIFO) stack, and support all four operations of an ordinary stack (push, top, pop ， and ， empty)

Implement MyStack class:

• Void push (int x): pushes an element to the top of the stack
• int pop(): returns the top element of the stack and removes it
• int top(): returns the stack top element
• boolean empty(): returns true if the stack is empty; Otherwise, false is returned.

be careful:

• You can only use the basic operations of the queue -- that is, push to back, peek/pop from front, size, and {is empty}.
• Your language may not support queues. You can use list or deque to simulate a queue, as long as it is a standard queue operation.

Thought arrangement

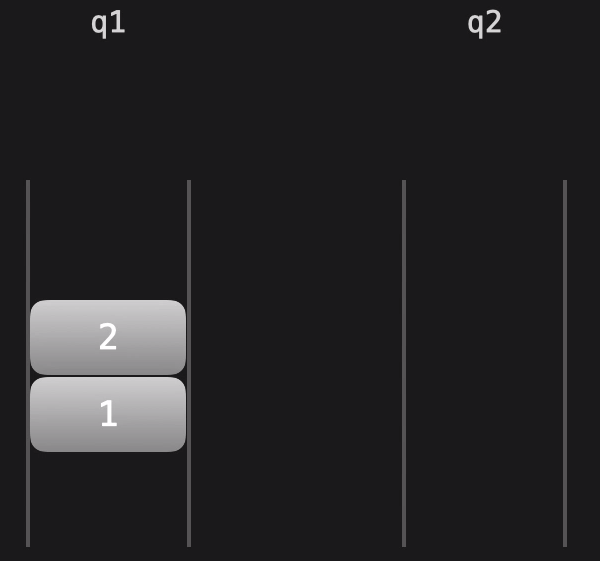
The premise of this idea: take the team head as the bottom of the stack and the team tail as the top of the stack.

• Create two new queues q1 and q2. q1 is used to store the required stack top and q2 is used to store the remaining data.

• MyStack stack = new MyStack();
  
  stack.push(1);
  stack.push(2);
  stack.top(); //Check the number of the number in the queue q1. If it is greater than 1, queue out the number in q1 to q2 in turn until there is one remaining number in q1, that is, top
  stack.pop();  /* Based on the previous step, the q1 The rest of the team, after the team q1 Empty, q2 Is the remainder in the queue, and q1 and q2 Exchange pointers, then q1 It's the same queue as before
  stack.empty();  // If both q1 and q2 are null, null is returned

  

• Time complexity:

        push: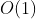

        pop: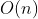

        top: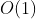

        empty: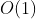

class MyStack {
public:
    queue<int> que1; //C + + Queue is a container adapter that gives programmers a first in first out (FIFO) data structure
    queue<int> que2;

    /** Initialize your data structure here. */
    MyStack() {

    }

    /** Push element x onto stack. */
    void push(int x) {
        que1.push(x);
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        top();    // There is one stack top element left in que1 and the rest in que2
        int res=que1.front();   // Stored in other variables, the in que1 can be deleted
        que1.pop();      // Delete the quantity in que1. At this time, que2 is the previous que1
        swap(que1,que2);   // Exchange the two and que1 restore the original
        return res;
    }
    
    /** Get the top element. */
    int top() {
        while((int)(que1.size())>1){      // Adding (int) here can reduce memory consumption
            que2.push(que1.front());    // front() returns the first element of the queue (the first element of the queue)
            que1.pop();      // pop() deletes the first element of the queue
        }
        return que1.front();     // The only element left in que1 is the top element of the stack
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return que1.empty()&&que2.empty();
    }
};

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

Single queue implementation method:

Premise: if the team head is the top of the stack, the complexity of entering the stack will become O(n).

During the stacking operation, first obtain the number of elements n before stacking, then queue the elements to the queue, and then queue the first n elements in the queue (i.e. all elements except the newly stacked elements) out of the queue and into the queue in turn. At this time, the elements at the front end of the queue are the newly stacked elements, and the front end and back end of the queue correspond to the top and bottom of the stack respectively.

class MyStack {
public:
    queue<int> q;

    /** Initialize your data structure here. */
    MyStack() {

    }

    /** Push element x onto stack. */
    void push(int x) {
        int n = q.size();
        q.push(x);
        for (int i = 0; i < n; i++) {
            q.push(q.front());
            q.pop();
        }
    }
    
    /** Removes the element on top of the stack and returns that element. */
    int pop() {
        int r = q.front();
        q.pop();
        return r;
    }
    
    /** Get the top element. */
    int top() {
        int r = q.front();
        return r;
    }
    
    /** Returns whether the stack is empty. */
    bool empty() {
        return q.empty();
    }
};

Time complexity: stack operation O(n), and other operations are O(1).
The stack operation needs to dequeue n elements in the queue and merge n+1 elements into the queue. There are 2n+1 operations in total. The time complexity of each dequeue and queue operation is O(1), so the time complexity of stack operation is O(n).
The out of stack operation corresponds to the out of queue of the front-end elements of the queue, and the time complexity is O(1).
The operation of obtaining the top element of the stack corresponds to obtaining the front element of the queue, and the time complexity is O(1).
To judge whether the stack is empty, you only need to judge whether the queue is empty, and the time complexity is O(1).

Advanced

Can you implement a stack with an average time complexity of O(1) for each operation? In other words, the total time complexity of performing n operations is O(n), although one of them may take longer than the others. You can use more than two queues.

3.3 design cycle queue

(LeeCode 622) design your circular queue implementation. Cyclic queue is a linear data structure whose operation performance is based on FIFO (first in first out) principle, and the tail of the queue is connected after the head of the queue to form a loop. It is also called "ring buffer".

One advantage of the circular queue is that we can use the space previously used by the queue. In a normal queue, once a queue is full, we cannot insert the next element, even if there is still space in front of the queue. But with circular queues, we can use this space to store new values.

Your implementation should support the following operations:

• MyCircularQueue(k): constructor that sets the queue length to K.
• Front: get the element from the team leader. If the queue is empty, - 1 is returned.
• Rear: get the tail element. If the queue is empty, - 1 is returned.
• enQueue(value): inserts an element into the circular queue. Returns true if successfully inserted.
• deQueue(): deletes an element from the circular queue. Returns true if the deletion was successful.
• isEmpty(): check whether the circular queue is empty.
• isFull(): check whether the circular queue is full.

Method 1: linked list

• No random search is required. You can apply for and delete new nodes at any time by using the linked list feature

Method 2: circular queue

• A circular queue is essentially a fixed size array, but the head and tail pointers of the queue can be moved cyclically.

Construction - O(1)

- define a static array of length k

- set up two pointers to the beginning and end of the queue respectively. In the initial state, the two pointers overlap

- use an additional variable to record the number of elements in the queue

Get first / last element - O(1)

- you need to judge whether the queue is empty

Insert - O(1)

- judge the length of the queue, and return false if it is full

- if there is still space, insert the element into the corresponding position of the tail pointer and add one to the tail pointer

- if the tail pointer exceeds the length of the static array, move to the beginning

- finally, add one to the size variable

Delete - O(1)

- judge the length of the queue. If it is empty, false will be returned

- if it is not empty, directly add one to the header pointer

- if the header pointer exceeds the length of the static array, move to the beginning

- finally, subtract the size variable by one

Thinking: if the queue space is full, how to expand it?

class MyCircularQueue {
public:
    /** Initialize your data structure here. Set the size of the queue to be k. */
    vector<int> q;
    int head, tail;
    int maxSize;
    int size;
    MyCircularQueue(int k) {
        q.resize(k, 0);  // Adjust the size of container q to k, and the value of each element after expansion is 0, which is 0 by default
        head = 0;
        tail = -1;    // During initialization, the tail pointer should overlap the head pointer, so as to facilitate insertion
        size = 0;    // Although the container capacity is k, it is empty, so size is equal to 0, not K
        maxSize = k;
    }
    
    /** Insert an element into the circular queue. Return true if the operation is successful. */
    bool enQueue(int value) {
        if (size == maxSize)
            return false;
        tail = (tail + 1) % maxSize;  // The small number is the remainder of the large number, and the result is the decimal itself
/*    1,Positive numbers are the remainder of negative numbers: that is, X% (- y) is equivalent to X% y
      2,Negative to positive remainder: that is (- x)% y is equivalent to - (x% y)
      3,Negative numbers are the remainder of negative numbers: that is (- x)% (- y) is equivalent to - (x% y)  */
        q[tail] = value;
        size++;
        return true;
    }
    
    /** Delete an element from the circular queue. Return true if the operation is successful. */
    bool deQueue() {
        if (size == 0)
            return false;
        head = (head + 1) % maxSize;
        size--;
        return true;
    }
    
    /** Get the front item from the queue. */
    int Front() {
        if (size == 0)
            return -1;
        return q[head];
    }
    
    /** Get the last item from the queue. */
    int Rear() {
        if (size == 0)
            return -1;
        return q[tail];
    }
    
    /** Checks whether the circular queue is empty or not. */
    bool isEmpty() {
        return size == 0;
    }
    
    /** Checks whether the circular queue is full or not. */
    bool isFull() {
        return size == maxSize;
    }
};

/**
 * Your MyCircularQueue object will be instantiated and called as such:
 * MyCircularQueue* obj = new MyCircularQueue(k);
 * bool param_1 = obj->enQueue(value);
 * bool param_2 = obj->deQueue();
 * int param_3 = obj->Front();
 * int param_4 = obj->Rear();
 * bool param_5 = obj->isEmpty();
 * bool param_6 = obj->isFull();
 */

3.4 sum of two numbers

(LeetCode 1) given an integer array num ， and an integer target value target, please find the two integers whose sum is the target value target ， in the array and return their array subscripts.

You can assume that each input will correspond to only one answer. However, the same element in the array cannot be repeated in the answer.

You can return answers in any order.

Violent solution - double loop enumeration

• For each number in the array, loop through other numbers to determine whether the sum of the two numbers is the target value
• Time complexity:

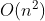
This is the simplest problem-solving idea, but it is not the optimal time complexity. In the process of problem-solving or interview, we need to give priority to ensure that our complexity is the best.

O(n) solution lookup table method

• While traversing, record some information to eliminate a layer of circulation, which is the idea of "space for time"
• There are two common implementations of lookup tables: ① hash table ② balanced binary search tree
• Traverse the array and create a HashMap to store the mapping between the number and its coordinate position
• For each number x in nums, find its corresponding number (target - x) in the HashMap. If there is a stored subscript, otherwise, insert the number and its subscript into the HashMap and return - 1 to ensure that it will not match itself.

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashtable;
        for (int i = 0; i < nums.size(); ++i) {
            auto it = hashtable.find(target - nums[i]); /* Find the element through the given primary key. If it is not found, it returns unordered_map::end  */
            if (it != hashtable.end()) {
                return {it->second, i};  /* it->second Value, i.e. index; It - > first key */
            }
            hashtable[nums[i]] = i;  /*Because we find the index through nums, that is, enter the number, and the array subscript is to be returned, the current number is stored in the hash table as the key and the index (array subscript) as the value */
        }
        return {};
    }
};

3.5 find the position of each number in the array for the first time

Given a one-dimensional array, find the position of the first occurrence of each number from left to right in the array. If this is the first occurrence, - 1 is returned

Example 1:

Input: [1,3,1,2,1]

Output: [- 1, - 1,0, - 1,0]

antic

No matter what the interview question is, you can consider whether there is any boundary before actually thinking about how to solve it. Giving priority to boundary situations is also a common skill in interviews,

- when there is no idea, you can open the topic to avoid cold air

- check that can prevent the final omission of boundary conditions

Violent solution - double loop enumeration

Check whether this number appears on the left of each number

• Enumerates all numbers in the array
• For each number, enumerate all the numbers before it
• If the same number is found in the second step, its subscript is returned directly, otherwise - 1 is returned

Through this question to give you some suggestions, even if it is a violent method, we also need to have such ideas and steps in our mind. Think about these steps first, which can help us clarify our ideas and clarify the details, and then write the code directly according to this idea. On the contrary, it's best not to think while writing, so if you don't think carefully, it may lead to the waste of the previous writing.

class Solution {
public:
    vector<int> find_left_repeat_num(vector<int>& nums) {
        vector<int> res;
        for (int i = 0; i < nums.size(); ++i) {
            int idx = -1;
            for(int j = 0;j < i;++j){
                if(nums[i] == nums[j]){
                    idx = j;
                    break;
                }
            }
            res.push_back(idx);
        }
        return res;
    }
};

O(n) solution lookup table method

• Use dict (unordered_map in C + +) to record the position of each number
• For each number, enumerate all the numbers before it
• Query whether the number exists in dict. If it exists, return its stored subscript. Otherwise, insert the number and its subscript into dict and return - 1

My solution:

	class Solution {
	public:
		vector<int> find_left_repeat_num(vector<int>& nums) {
			unordered_map<int, int> mp;
			vector<int> res;
			for (int i = 0; i < nums.size(); ++i) {
				auto it = mp.find(nums[i]);
				if (it == mp.end()) {
					mp[nums[i]] = i;
					res.push_back(-1);
				}
				else
					res.push_back(it->second);

			}
			return res;
		}

	};

Official explanation:

class Solution {
public:
    vector<int> find_left_repeat_num(vector<int>& nums) {
        unordered_map<int, int> mp;
        vector<int> res;
        for (int i = 0; i < nums.size(); i++) {
            if (!mp.count(nums[i])) {
                mp[nums[i]] = i;
                res.push_back(-1);
            } else {
                res.push_back(mp[nums[i]]);
            }
        }
        return res;
    }
};

unordered_map Medium:
use count，Returns the number of elements to be found. If yes, return 1; Otherwise, 0 is returned.
use find，Returns the location of the element to be found. If not, returns map.end().