In a row of dominoes, A[i] and B[i] represent the top half and bottom half of the ith dominoes, respectively. (a domino is composed of two numbers from 1 to 6 that are tiled in the same column - one on each half of the tile.)

We can rotate the i-th domino so that the values of A[i] and B[i] are exchanged.

Returns the minimum number of rotations that can make all values in A or all values in B the same.

If not, return to -1

 

Example 1:

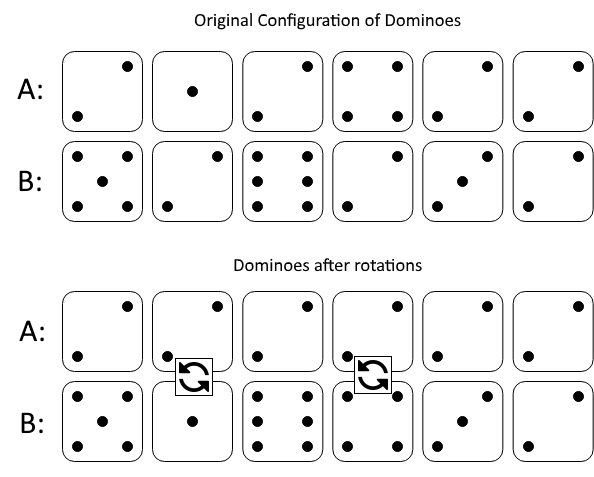
Input: A = [2,1,2,4,2,2], B = [5,2,6,2,3,2]
Output: 2
 Interpretation:
Figure 1 shows the dominoes given by A and B before we rotate.
If we rotate the second and fourth dominoes, we can make each value in the above row equal to 2, as shown in Figure 2.

Example 2:

Input: A = [3,5,1,2,3], B = [3,6,3,3,4]
Output: -1
 Interpretation:
In this case, it is not possible to rotate the domino to make a row equal.

 

Tips:

1 <= A[i], B[i] <= 6

2 <= A.length == B.length <= 20000

C++

class Solution {
public:
    int minDominoRotations(vector<int>& A, vector<int>& B) 
    {
        int n=A.size();
        int m=B.size();
        if(m!=n)
        {
            return -1;
        }
        vector<int> tmp(7,0);
        for(int i=0;i<n;i++)
        {
            if(A[i]==B[i])
            {
                tmp[A[i]]++;
            }
            else
            {
                tmp[A[i]]++;
                tmp[B[i]]++;
            }
        }
        int flag=1;
        int val=0;
        for(int i=1;i<=6;i++)
        {
            if(n==tmp[i])
            {
                val=i;
                flag=0;
                break;
            }
        }
        if(flag)
        {
            return -1;
        }
        else
        {
            int up=0;
            int same=0;
            for(int i=0;i<n;i++)
            {
                if(A[i]==B[i])
                {
                    same++;
                }
                else
                {
                    if(val==A[i])
                    {
                        up++;
                    }
                }
            }
            return min(up,n-same-up);

        }
    }
};

python

class Solution:
    def minDominoRotations(self, A: List[int], B: List[int]) -> int:
        n=len(A)
        m=len(B)
        if m!=n:
            return -1
        tmp=[0 for i in range(7)]
        for i in range(n):
            if A[i]==B[i]:
                tmp[A[i]]+=1
            else:
                tmp[A[i]]+=1
                tmp[B[i]]+=1
        flag=1
        val=0
        for i in range(1,7):
            if n==tmp[i]:
                flag=0
                val=i
                break
        if flag:
            return -1
        else:
            up=0
            same=0
            for i in range(n):
                if A[i]==B[i]:
                    same+=1
                else:
                    if A[i]==val:
                        up+=1
            return min(up,n-same-up)