Given a Binary Tree
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val) {
val = _val;
}
public Node(int _val, Node _left, Node _right, Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/Fill in each of its next pointers so that it points to its next right node. If the next right node cannot be found, set the next pointer to NULL.
Initially, all next pointers are set to NULL.
Advanced:
- You can only use constant extra space.
- The use of recursive solutions also meets the requirements, and the stack space occupied by recursive programs in this topic does not count as additional space complexity.
Example:
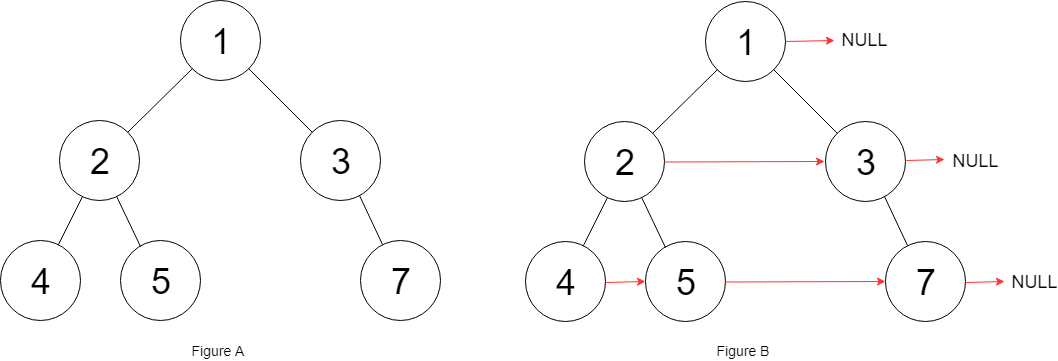
Input: root = [1,2,3,4,5,null,7] Output: [1, #, 2,3, #, 4,5,7, #] Interpretation: Given a binary tree as shown in Figure A, your function should populate each of its next pointers to its next right node, as shown in Figure B. The serialized output is in a hierarchical traversal order (connected by the next pointer),'#'denotes the end of each layer.
Tips:
- The number of nodes in the tree is less than 6000
- -100 <= node.val <= 100
Method 1: Hierarchical traversal
Organize the points at each level of a binary tree into a chain table, and the intuitive idea is to traverse through the layers. Hierarchical traversal of a tree is based on a breadth-first search. It traverses a binary tree in the order of layers. Before traversing layer i, it must traverse layer i - 1.
algorithm
- Initialize a queue q to place the root node in the queue. When the queue is not empty, record the current queue size as n, take n elements out of the queue, and expand new nodes through these n elements. Loop like this until the queue is empty.
- You can ensure that n points are on the same layer each time you traverse. You can modify the next pointer of this layer's nodes as you traverse each layer, so that each layer can be organized into a chain table.
Complexity analysis
- Note that the number of points on the tree is N.
- Time complexity: O(N). All the points on this tree need to be traversed.
- Spatial Complexity: O(N). This is the space cost of the queue.
class Solution {
public Node connect(Node root) {
// level traversal
if(root == null){
return null;
}
Queue<Node> queue = new LinkedList<>();
queue.offer(root); // Root node enqueued
while(!queue.isEmpty()){
// Record the size of the current queue
int curLen = queue.size();
// Request a null node pointer
Node last = null;
// Traverse from the first in the queue
for(int i = 0; i < curLen; i ++){
// Current Counter Element Queued
Node cur = queue.poll();
// If left and right children are not empty, join the queue
if(cur.left != null){
queue.offer(cur.left);
}
if(cur.right != null){
queue.offer(cur.right);
}
// Build from left to right. Connection relationship for next
if(i != 0){
last.next = cur;
}
last = cur;
}
}
return root;
}
}class Solution {
public Node connect(Node root) {
// level traversal
if(root == null){
return null;
}
Queue<Node> queue = new LinkedList<>();
queue.offer(root); // Root node enqueued
while(!queue.isEmpty()){
// Record the size of the current queue
int curLen = queue.size();
// Request a null node pointer
Node tempNode = null;
// Traverse from the first in the queue
for(int i = 0; i < curLen; i ++){
// Current Counter Element Queued
Node cur = queue.poll();
// If left and right children are not empty, join the queue
if(cur.right != null){
queue.offer(cur.right);
}
if(cur.left != null){
queue.offer(cur.left);
}
// Build from right to left. next's join relationships, traversed in reverse order
cur.next = tempNode;
tempNode = cur;
}
}
return root;
}
}Method 2: Reduce spatial complexity by using the established next pointer
- If a next pointer is already established between the layers I nodes, all the nodes in that layer can be accessed through the next pointer. At the same time, for each layer I node, its child nodes in layer i+1 can be known through its left and right pointers, so the next pointer can be established sequentially for the layers i+1 nodes during traversal.
- Start at the root node. Layer 0 has only one node and does not need to be processed. Next pointers can be created for the next layer from the previous layer.
- Create a next pointer for layer x+1 when it is in layer X. Once these connection operations are completed, move to Layer x+1 to create a next pointer for Layer x+2.
- When a layer node is traversed, its next pointer is established. This saves space by eliminating the need for queues. Each time you know the leftmost node of the next layer, you can start at that node and traverse all the nodes of that layer as you would a chain table.
Complexity analysis
- Time complexity: O(N).
- Spatial complexity: O(1).
class Solution {
Node nextStart = null; // Starting position of each layer
Node tempNext = null; // Position Subscript After Each Layer Moves Backward
public Node connect(Node root) {
// Use the established next pointer as an aid to establish the next level of relationship from the upper level information
if(root == null){
return null;
}
Node curStart = root; // Start at the root node
while(curStart != null){
nextStart = null;
tempNext = null;
for(Node p = curStart; p != null; p = p.next){
if(p.left != null){
doConnect(p.left);
}
if(p.right != null){
doConnect(p.right);
}
}
// Transfer the header node to the leftmost element in the next layer to establish the n+1 layer relationship
curStart = nextStart;
}
return root;
}
public void doConnect(Node p){
// Record the location of the node currently connected, and connect directly when there are subsequent elements
if(tempNext != null){
tempNext.next = p;
}
// Record the leftmost head element of n+1 layer
if(nextStart == null){
nextStart = p;
}
tempNext = p;
}
}class Solution {
// Recursive Solution
public Node connect(Node root) {
if(root == null) {
return null;
}
// If the right subtree is not empty, the next of the left subtree is the right subtree
if(root.left != null && root.right != null) {
root.left.next = root.right;
}
// If the right subtree is empty, the next of the left subtree is derived from the next of the root node
if(root.left != null && root.right == null){
root.left.next = getNode(root.next);
}
// The next XT of the right subtree is derived from the next of the root node
if(root.right != null){
root.right.next = getNode(root.next);
}
// Make sure root first. The nodes under right are fully connected because root. Connection of nodes under left
// Root is required. Left. Next node information, if root. Nodes under right are not fully connected
// Next (that is, recursively to root.left first), the information chain under root.left.next is incomplete, and the
// Returns the wrong information. Possible error situations are shown in the following figure. At this point, the bottom leftmost node will have no
// Method to get the correct next information:
// o root
// / \
// root.left o - o root.right
// / / \
// o - o o
// / / \
// o o o
connect(root.right);
connect(root.left);
return root;
}
private Node getNode(Node node) {
while (node != null) {
if (node.left != null) {
return node.left;
}
if (node.right != null) {
return node.right;
}
node = node.next;
}
return null;
}
}