subject

Give you the head node of the linked list. Please arrange it in ascending order and return the sorted linked list.

Example 1:

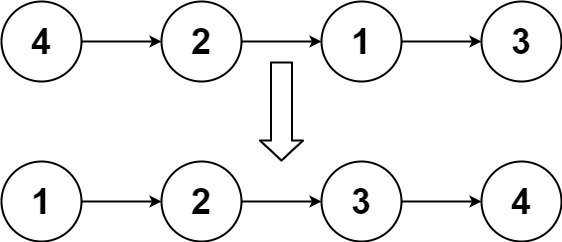
Input: head = [4,2,1,3]
Output: [1,2,3,4]

Example 2:

Input: head = [-1,5,3,4,0]
Output: [- 1,0,3,4,5]

Example 3:

Input: head = []
Output: []

Tips:

• The number of nodes in the linked list is in the range [0, 5 * 104]
• -105 <= Node.val <= 105

Advanced: can you sort the linked list under O(n log n) time complexity and constant space complexity?

It is still difficult to sort the linked list. Here is an idea: first traverse the linked list to get the number of elements, then apply for the space of the corresponding number with malloc, store all the linked list elements in the applied array, and sort the array with some sorting methods (fast sorting, Hill sorting, heap sorting, etc.), Then write the ordered data back to the linked list.

Here I do not use the above ideas, but directly operate the linked list, so as to achieve the purpose of ranking the linked list. Both recursive and non recursive code ideas are merge sorting.

recursion

thinking

1. Find the midpoint of the linked list, take the midpoint as the boundary, and split the linked list into two sub linked lists.

2. Sort the two sub linked lists separately.

3. Merge the two sorted sub linked lists to obtain a complete sorted linked list.

The above process can be implemented recursively. The termination condition of recursion is that the number of nodes in the linked list is less than or equal to 1, that is, when the linked list is empty or the linked list contains only 1 node, there is no need to split and sort the linked list.

The fast and slow pointer can be used to find the midpoint of the linked list. The fast pointer moves 2 steps at a time and the slow pointer moves 1} step at a time. When the fast pointer reaches the end of the linked list, the linked list node pointed to by the slow pointer is the midpoint of the linked list.

Merging two linked lists can use the tail insertion method to continuously tail the nodes after the given header.

code

struct ListNode* Mergedata(struct ListNode* head1,struct ListNode* head2){//Merge two ordered linked lists
    struct ListNode s;//Given chain header
    struct ListNode* cur=&s;//Head pointer, pointing to the chain header
    while(head1&&head2){//Insert the tail of two ordered linked lists after s
        if(head1->val<=head2->val){
            cur->next=head1;
            head1=head1->next;
        }else{
            cur->next=head2;
            head2=head2->next;
        }
        cur=cur->next;
    }
    if(head1){//Tail insertion remainder
        cur->next=head1;
    }else{
        cur->next=head2;
    }
    return s.next;
}
struct ListNode* Middle(struct ListNode* head){
    //Find the middle node of the linked list and return the address. Note that this function will divide a linked list into two.
    struct ListNode* prev=NULL;
    struct ListNode* slow=head;
    struct ListNode* fast=head;
    while(fast&&fast->next){
        prev=slow;
        slow=slow->next;
        fast=fast->next->next;
    }
    prev->next=NULL;
    return slow;
}
struct ListNode* sortList(struct ListNode* head){
    if(head==NULL||head->next==NULL){
        return head;
    }
    struct ListNode* cur=Middle(head);//Get the intermediate node address
    head=sortList(head);//Put the first half in order
    cur=sortList(cur);//Put the second half in order
    return Mergedata(head,cur);//Merge the front and rear parts
}

 

After reading the above code and using recursion, you will find that this problem is actually the integration of merging two ordered linked lists, finding the middle node of the linked list and merging and sorting.

Complexity analysis

Time complexity: merge and sort. The time complexity is O(NlogN).

Spatial complexity: the recursion depth is logN, so the spatial complexity is O(logN).

non-recursive

Because the space complexity of the advanced problem is O(1), it is obvious that the above recursive code does not meet the requirements. Then we need to find a way to turn recursion into a loop.

thinking

First get the length len of the linked list, and then split the linked list into sub linked lists for merging.

The specific methods are as follows:

1. Use step to represent the length of the sub linked list to be sorted each time. Initially, step=1;

2. Each time, the linked list is divided into several sub linked lists with the length of step (the length of the last sub linked list can be less than step), and each two sub linked lists are combined in a group. After the combination, several ordered sub linked lists with the length of 2*step can be obtained (the length of the last sub linked list can be less than 2*step).

3. Double the value of step, repeat step 2, and merge the longer ordered sub linked list until the length of the ordered sub linked list is greater than or equal to len, and the whole linked list is sorted.

code

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode* Mergedata(struct ListNode* head1,struct ListNode* head2){//Merge two ordered linked lists
    struct ListNode s;
    struct ListNode* cur=&s;
    while(head1&&head2){
        if(head1->val<=head2->val){
            cur->next=head1;
            head1=head1->next;
        }else{
            cur->next=head2;
            head2=head2->next;
        }
        cur=cur->next;
    }
    if(head1){
        cur->next=head1;
    }else{
        cur->next=head2;
    }
    return s.next;
}
struct ListNode* Disconnect(struct ListNode* head,int step){
    //Split the linked list according to the length of step and return the address of the remaining part after splitting
    if(head==NULL){
        return NULL;
    }
    struct ListNode* cur=head;
    for(int i=0;head&&i<step;i++){
        cur=head;
        head=head->next;
    }
    cur->next=NULL;
    return head;
}
int Length(struct ListNode* head){//Find the length of the linked list
    int count=0;
    while(head){
        head=head->next;
        count++;
    }
    return count;
}
struct ListNode* sortList(struct ListNode* head){
    struct ListNode s;//Given node, convenient tail insertion
    struct ListNode* cur=&s;//Point to the given header node
    cur->next=head;//First connect the given linked list, which must be done
    int len=Length(head);
    for(int step=1;step<len;step*=2){//Step < len, merge and sort continue
        head=s.next;//Update head
        cur=&s;//Update cur
        while(head){//Each step is grouped and merged until the head is empty
            struct ListNode* h1=head;//Get the first part after splitting
            struct ListNode* h2=Disconnect(h1,step);//Get the second part after splitting
            head=Disconnect(h2,step);//Get the rest after splitting
            cur->next=Mergedata(h1,h2);//Merge the first and second parts and insert them after s
            while(cur->next){//cur go ahead for the next tail insertion
                cur=cur->next;
            }
        }
    }
    return s.next;
}

Complexity analysis

Time complexity: merge and sort. The time complexity is O(NlogN).

Space complexity: no additional space is applied, and the space complexity is O(1).