Example 1: 77 combination

77. Portfolio
This question is mainly to understand the basic use of backtracking algorithm. Take the given n=4,k=2 as an example

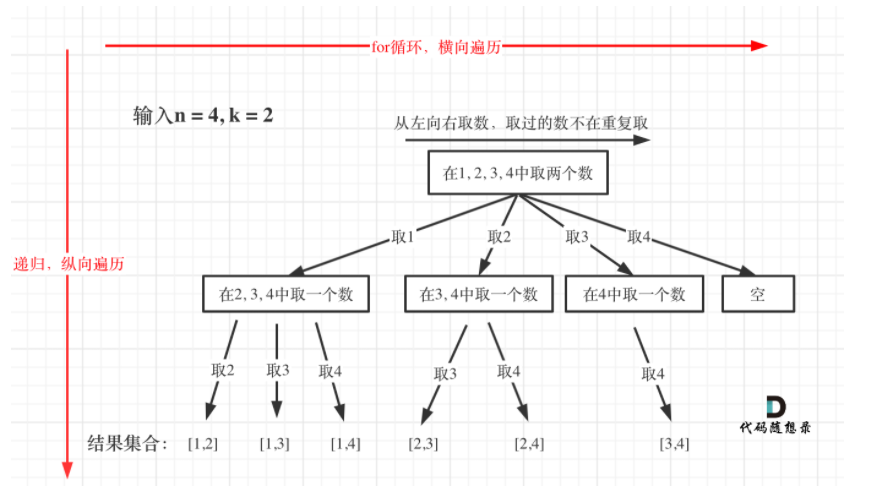
(source: Code Capriccio)

As can be seen from the above figure, the logic of the code is to insert for loop traversal in recursion. The exit condition of a recursive loop is when the path length reaches k. However, there are some small errors in the coding process, such as my first version of the code:

Wrong version

class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        res=[]
        path=[]
        def dfs(n,k,indx):
            if len(path)==k:
                res.append(path)
                return
            for i in range(indx,n):
                path.append(i)
                dfs(n,k,i+1)
                path.pop()

        dfs(n,k,1)
        return res

The first problem is that res.append(path) is a shallow copy of path. Res will change every time the path changes, so the final res is an empty array. The correct writing should be res.append(path [:]);
In this way, the number "for" in "is not correct. The reason why it is written as for i in range(indx,n):, is because I'm a little confused about what dfs(n,k,n+1) will get in the for loop. Think carefully about the situation if len(path)==k is not satisfied. At this time, because indx is n+1 and can't enter the for loop, dfs(n,k,n+1) will jump naturally.

Correct version:

class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        res=[]
        path=[]
        def dfs(n,k,indx):
            if len(path)==k:
                res.append(path[:])
                return
            for i in range(indx,n+1):
                path.append(i)
                dfs(n,k,i+1)
                path.pop()

        dfs(n,k,1)
        return res

There is still room for optimization in the above code. For example, for the case of n = 4 and K = 4, only [1,2,3,4] meets the requirements. Other cases with 2, 3 and 4 as the starting position are not enough for the number of elements we need, so there is no need to search. In this case, pruning method can be used to optimize.

	Assume the number of elements that have been selected: len(path),Then the number of elements needed is: k - len(path). Then in the collection n At most from this starting position : n - (k - len(path)) + 1 Start traversal from greater than n - (k - len(path)) + 1 The number of elements will be insufficient at the beginning of traversal, so there is no need to traverse

(more detailed description: Code Capriccio)

Pruning optimized version:

Note here that n - (k - len(path)) + 1 is taken, so it is written as n - (k - len(path)) + 2;
It can be found that the execution time is greatly reduced

class Solution(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        res=[]
        path=[]
        def dfs(n,k,indx):
            if len(path)==k:
                res.append(path[:])
                return
            for i in range(indx,n - (k - len(path)) + 2):
                path.append(i)
                dfs(n,k,i+1)
                path.pop()

        dfs(n,k,1)
        return res

Example 2: 306 Cumulative addend

306. Addenda
This question is the same logic as the previous one, but it's more mental than the previous one.
First, there are three steps:

1, Variables to be determined.

num must be required; index used to point to the current number;
The number is currently the count of the feasible number (only count > = 2 meets the condition of cumulative number);
It also refers to prevprev of the previous number and prev of the previous number, as well as the current number being determined

2, Single layer logic

First assume that the current number current is 0, I get len(num) from the index pointing to the current number, turn num[i] into int, and try to attach it to current, current=current*10+int(num[i]). When the effective number is greater than or equal to two, that is, when count > = 2, if the current current < (prevprev + prev), it indicates that the current number is not large enough, and it may be necessary to get the next number, so continue the cycle; If current > (prevprev + prev), it indicates that the current number is unqualified and directly returns false.
When count < 2 or current==(prevprev+prev), you need to judge if dfs(num,i+1,count+1,prev,current)
Take "199100" as an example. If count < 2, first treat the initial number "1" as an independent number, and then treat the subsequent "9" as an independent number. prevprev=1,prev=9,current=9. At this time, current > (prevprev + prev), so return False, that is, dfs(num,2,2,9,9) is False, the for loop continues, current becomes 99, and continues down
current==(prevprev+prev), continue to search

3, Conditions for exiting recursion

When index > = len (Num) and count > 2, it indicates that you can exit normally and return True
If index > = len (Num) is reached, and the valid number is not greater than 2, return false (such as "19910")

class Solution(object):
    def isAdditiveNumber(self, num):
        """
        :type num: str
        :rtype: bool
        """

        n=len(num)
        # if n<3:
        #     return False

        def dfs(num,index,count,prevprev,prev):
            if index>=len(num):
                if count>2:
                    return True
                else:
                    return False
                # return count>2

            current=0
            for i in range(index,len(num)):
                c=num[i]
                if num[index]=='0' and i>index:
                    return False

                current=current*10+int(c)

                if count>=2:
                    if current>(prevprev+prev):
                        return False
                    if current<(prevprev+prev):
                        continue

                if dfs(num,i+1,count+1,prev,current):
                    return True
               
            return False

        return dfs(num,0,0,0,0)