subject


Method 1: dichotomy + prefix and
Algorithm flow:
- Data preprocessing: scan the string s from front to back, record the candle subscript in the array list (the array is strictly incremented - binary basis), and preprocess the prefix and array of the plate
- Traverse queries:
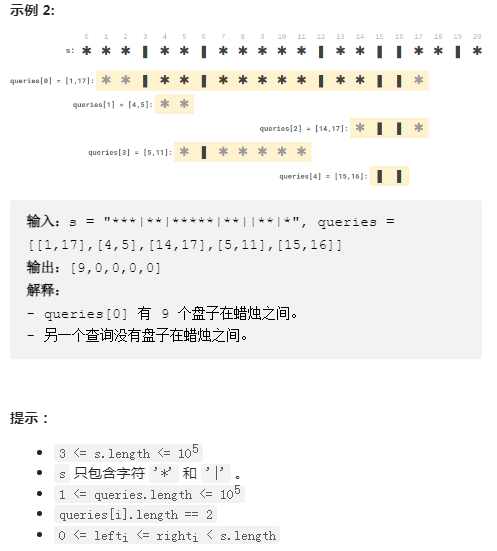
- For any query [ a , b ] [a,b] For [a,b], find out the right candle c closest to a and the left candle d closest to B respectively. This operation can be realized by bisecting the array list and querying the interval [ c , d ] [c, d] The "number of plates in [c,d] operation can directly query the" prefix and "array
class Solution {
public int[] platesBetweenCandles(String s, int[][] queries) {
int n = s.length();
int m = queries.length;
int[] res = new int[m];
int[] preSum = new int[n];
List<Integer> list = new ArrayList<>();
// Data preprocessing
for (int i = 0, sum = 0; i < n; i++) {
if (s.charAt(i) == '*') {
sum++;
}
// Record the subscript of the candle
if (s.charAt(i) == '|') {
list.add(i);
}
// Prefix and
preSum[i] = sum;
}
if (list.size() == 0) {
// No candles
return res;
}
// Traversal queries
for (int i = 0; i < m; i++) {
int a = queries[i][0], b = queries[i][1];
int c = -1, d = -1;
// Find the nearest candle to the right of a
int l = 0, r = list.size() - 1;
while (l < r) {
int mid = l + (r - l) / 2;
if (list.get(mid) < a) {
l = mid + 1;
} else {
r = mid;
}
}
if (list.get(r) >= a) {
c = list.get(r);
} else {
// non-existent
continue ;
}
// Find b the nearest candle on the left
l = 0;
r = list.size() - 1;
while (l < r) {
int mid = l + (r - l + 1) / 2;
if (list.get(mid) > b) {
r = mid - 1;
} else {
l = mid;
}
}
if (list.get(r) <= b) {
d = list.get(r);
} else {
// non-existent
continue ;
}
if (c <= d) {
res[i] = preSum[d] - preSum[c];
}
}
return res;
}
}
- Time complexity: let the length of s be n n n. The length of queries is m m m. The complexity of counting all candles and storing them in the list is O ( n ) O(n) O(n); Preprocessing prefix and array complexity is O ( n ) O(n) O(n); The number of candles to be inquired is up to two n n n) , complexity is O ( log n ) O(\log{n}) O(logn), shared m m m queries need to be processed, with a complexity of O ( m ∗ log n ) O(m * \log{n}) O(m∗logn). The overall complexity is O ( n + m log n ) O(n + m\log{n}) O(n+mlogn)
- Space complexity: O ( n ) O(n) O(n)
Method 2: prefix and
On the premise of given s, the nearest candle on the left and right of each position is uniquely determined. In addition to the preprocessing prefix and, the nearest candle subscript on the left and right of each position can also be preprocessed, so as to save two points each time.
Algorithm flow:
-
Data preprocessing:
- Prefix array: prefix and array, recording from interval [ 0 , i ] [0,i] Number of * of [0,i]
- leftCandle array: record the nearest candle to the left of position i
- rightCandle array: record the nearest candle to the right of position i
-
Traversal queries:
- For any query [ a , b ] [a,b] In terms of [a,b], use rightCandle and leftCandle respectively to O ( 1 ) O(1) O(1) time complexity find the nearest candle on the right of a and the nearest candle on the left of b, and then calculate the number of plates by using the prefix of prefix and array (through preprocessing, the time complexity of finding candles and calculating the number of plates is reduced to O ( 1 ) O(1) O(1))
class Solution {
public int[] platesBetweenCandles(String s, int[][] queries) {
int n = s.length();
// Prefix [i] stands for the number of plates in [0,i]
int[] preSum = new int[n];
for (int i = 0, sum = 0; i < n; i++) {
if (s.charAt(i) == '*') {
sum++;
}
preSum[i] = sum;
}
// leftCandle[i] indicates the nearest candle position to the left of I
// If I there is no candle on the left, leftCandle[i] = -1;
int[] leftCandle = new int[n];
for (int i = 0, l = -1; i < n; i++) {
if (s.charAt(i) == '|') {
l = i;
}
leftCandle[i] = l;
}
// rightCandle[i] indicates the nearest candle position to the right of I
// If I has no candle on the right, then rightCandle[i] = -1;
int[] rightCandle = new int[n];
for (int i = n - 1, r = -1; i >= 0; i--) {
if (s.charAt(i) == '|') {
r = i;
}
rightCandle[i] = r;
}
int[] res = new int[queries.length];
// Traversal queries
for (int i = 0; i < queries.length; i++) {
int x = rightCandle[queries[i][0]];
int y = leftCandle[queries[i][1]];
res[i] = (x == -1 || y == -1 || x >= y) ? 0 : preSum[y] - preSum[x];
}
return res;
}
}
- Time complexity: O ( n + q ) O(n + q) O(n+q), where n n n is the length of the array, q q q is the number of inquiries
- Space complexity: O ( n ) O(n) O(n), where n n n is the length of the array. need O ( n ) O(n) The space of O(n) saves the results of preprocessing