216. Combined sum III

Problem Description: Portal

Idea:

As long as you understand this question Leetcode 77 There will be a general idea.

In this question, k is the depth of the tree.
9 is the width of the tree.

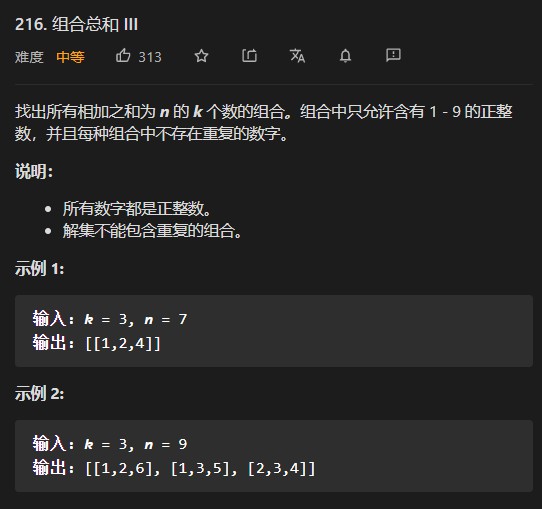
For example, if k=2 and n=4, it is to find the combination of K (number) = 2 and n (sum) = 4 in the set [1, 2, 3, 4, 5, 6, 7, 8, 9].

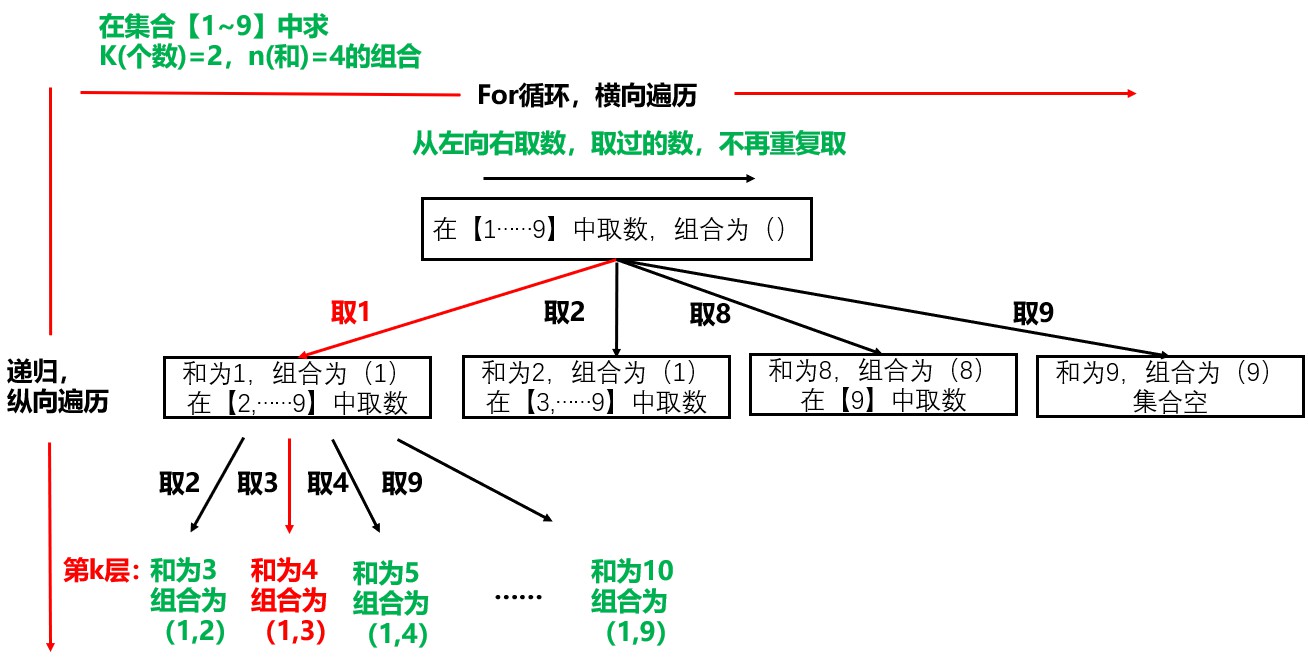
It can be seen from the figure that only the sum is 4 and the combination is (1,3).

1. Determining recursive function parameters
path stores the qualified results, and result stores the result set.
Path refers to the path from a root node to a leaf node.

vector<vector<int>> result; // Store result set 
vector<int> path; // Qualified results

The following parameters are also required:

1. targetSum (int) target sum, that is, n in the title.
2. k (int) is the set of k numbers required in the title.
3. Sum (int) is the sum of the collected elements, that is, the sum of the elements in the path.
4. startIndex (int) is the starting position of the next for loop search.

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex) 

In fact, the parameter sum can be omitted here. Each time targetsum subtracts the value of the selected element, and then judge that if targetsum is 0, it indicates that qualified results have been collected.
For ease of understanding, add a sum parameter.

In fact, it is difficult to determine the parameters of recursive functions at one time. Generally, write logic first, and then fill in what parameters are needed.

2. Determine termination conditions
K actually limits the depth of the tree, so if path Size () = k, it terminates.
If the element sum collected in the path is the same as the targetSum at this time, it is the result that collects the current result.

if (path.size() == k) {
    if (sum == targetSum) 
    	result.push_back(path);
    return; 
    // If path Size () = = K but sum= Targetsum returns directly
}

In the process of single-layer search, the set is fixed with 9 numbers [1... 9], so the for loop is fixed with I < = 9

The processing logic is that the path collects the elements selected each time, which is equivalent to the edges in the tree structure,
Sum to count the sum of elements in the path.

for (int i = startIndex; i <= 9; i++) {
    sum += i;
    path.push_back(i);
    backtracking(targetSum, k, sum, i + 1); // Note that i+1 adjusts startIndex
    sum -= i; // to flash back 
    path.pop_back(); // to flash back 
}

When self increment is required when processing logic,
Backtracking should correspond one by one,
Perform self subtraction.

3. Overall thinking

class Solution {
private:
    vector<vector<int>> result; 
    // Store result set 
    vector<int> path; 
    // Qualified results
    // targetSum: target sum, that is, n in the title. 
    // k: The set of K numbers required in the title. 
    // Sum: the sum of the collected elements, that is, the sum of the elements in the path. 
    // startIndex: the starting position of the next for loop search.
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; // If path Size () = = K but sum= Targetsum returns directly
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; // handle
            path.push_back(i); // handle
            backtracking(targetSum, k, sum, i + 1); // Note that i+1 adjusts startIndex
            sum -= i; // to flash back
            path.pop_back(); // to flash back
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // Can not add
        path.clear();   // Can not add
        backtracking(n, k, 0, 1);
        return result;
    }
};

Pruning optimization results

Prune and optimize the unqualified results.

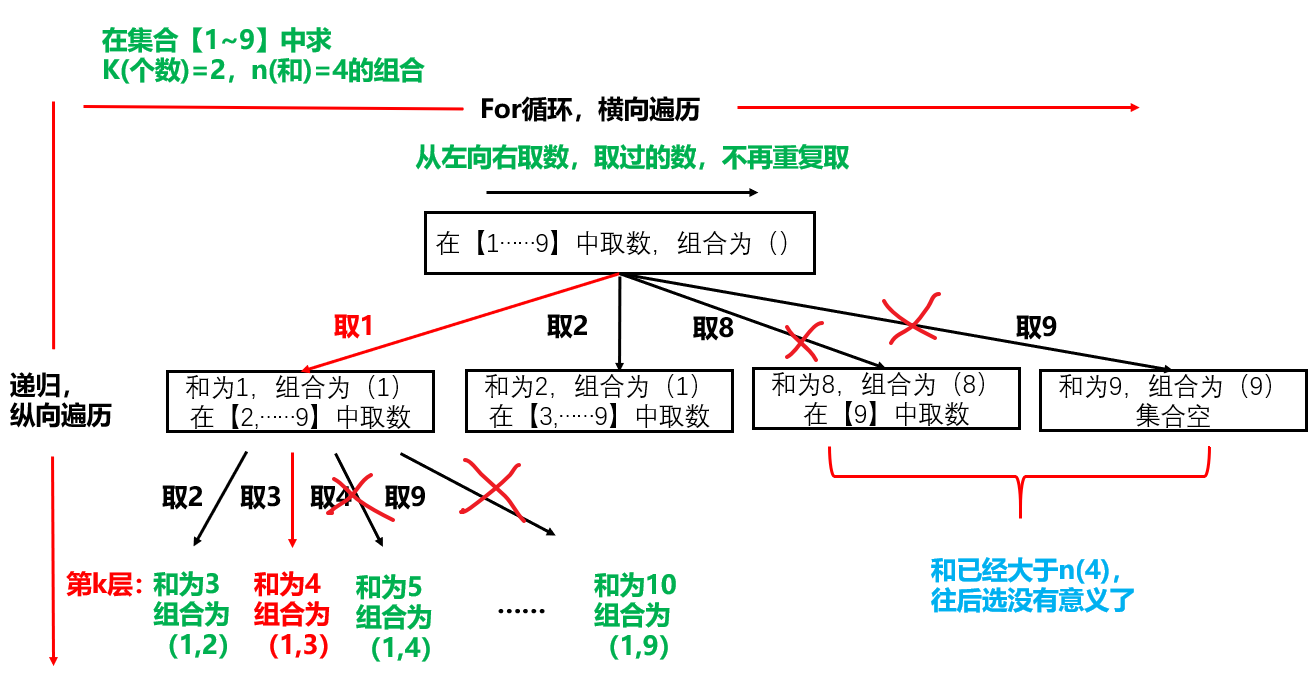
In fact, the selected elements are greater than n,
Subsequent direct pruning.
The pruning place is where the recursion terminates. The code is as follows:

if (sum > targetSum) { // Pruning operation
    return;
}

Finally, the C + + code is as follows:

class Solution {
private:
    vector<vector<int>> result; // Store result set
    vector<int> path; // Qualified results
    // targetSum: target sum, that is, n in the title.
    // k: The set of K numbers required in the title.
    // Sum: the sum of the collected elements, that is, the sum of the elements in the path.
    // startIndex: the starting position of the next for loop search.
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (sum > targetSum) { // Pruning operation
            return; // If path Size () = = K but sum= Targetsum returns directly
        }
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return;
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; // handle
            path.push_back(i); // handle
            backtracking(targetSum, k, sum, i + 1); // Note that i+1 adjusts startIndex
            sum -= i; // to flash back
            path.pop_back(); // to flash back
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // Can not add
        path.clear();   // Can not add
        backtracking(n, k, 0, 1);
        return result;
    }
};

Does it feel clear.
Today reminds me of a speech by jobs at Stanford University.

I very much agree with everything in the speech. Unfortunately, I didn't see it until I was about to graduate.
If I had seen some earlier, it might have been more helpful for me to make life choices.

I'm about to graduate and go to work. Give me a word:

Work will occupy a large part of your life
Your work is going to fill a large part of your life
Only by believing that what you do is great work can you be happy
and the only way to be truly satisfied is to do what you believe is great work
And great work comes from your love
And the only way to do great work is to love what you do
If you haven't found it yet
If you haven't found it yet
Keep looking, don't stop
Keep looking and don't settle
Search wholeheartedly
As with all matters of the heart
When you meet it, you will understand
You'll know when you find it
Like those beautiful love
And like any great relationship
With the passage of years, it becomes more mellow and beautiful
it just gets better and better as the years roll on
So keep looking and never stop!
So keep looking, don't settle