Title Requirements

Link to the original title: 23. Merge K Ascending Chain Lists

The Title requirements are as follows:

Give you an array of lists, each in ascending order.

Please merge all lists into one ascending list and return the merged list.

Examples are as follows:

Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Interpretation: The chain list array is as follows:
[
1->4->5,
1->3->4,
2->6
]
Merge them into an ordered list.
1->1->2->3->4->4->5->6

The ListNode node structure is as follows:

  public class ListNode {
      int val;
      ListNode next;
      ListNode() {}
      ListNode(int val) { this.val = val; }
      ListNode(int val, ListNode next) { this.val = val; this.next = next; }
  }

Solution: Merge

thinking

Looking at the problem description first, it is not difficult to see that the sub-problem of this problem is to merge two ordered chain lists. So, first solve the problem of merging two ordered chain lists, and then consider how to merge several ordered chain lists.

Merge two ordered chains

Merging two ordered chain lists requires an additional chain header head, because a chain table is ordered, it only needs to traverse through the two chains from the beginning and compare the values of the nodes of the two chains, insert the nodes with smaller value directly into the chain header, and proceed thereafter until one chain table has been traversed, and then connect the rest of the other chain table directly to the end of the new chain table.

The merge process is illustrated as follows:

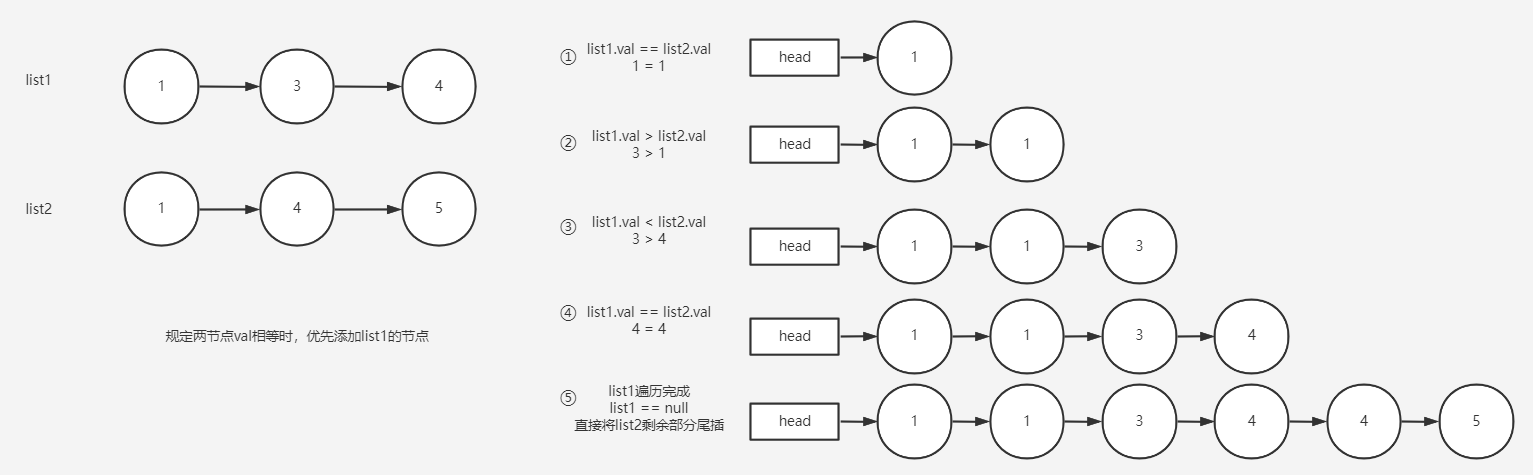
The method code for merging two linked lists is as follows:

	public ListNode mergeList(ListNode list1, ListNode list2){
        ListNode head = new ListNode();
        ListNode last = head;
        while(list1 != null && list2 != null){
            if(list1.val <= list2.val){
                last.next = list1;
                list1 = list1.next;
            }else{
                last.next = list2;
                list2 = list2.next;
            }
            last = last.next;
        }
        if(list1 != null) last.next = list1;
        if(list2 != null) last.next = list2;
        return head.next;
    }

Merging Ordered Chain Lists Directly

The easiest and simplest way to think about it is to set a new list result, which can be initially assigned to lists[0], then iterate through the lists array, merge each iterated list[i] with the result, and merge the results directly after the iteration.

Complexity analysis

Time complexity: O(k) ² N) Set the maximum length of each list in the chain list array to be your n. The length of the resultlist is n for the first merge and 2 for the second merge × N, you can infer that the length of the result at the kth merge is k × N, and a total of K merges are required. Therefore, the total time cost is O(n) × (1+k) / 2 × K).
Spatial Complexity: O(1), Direct Merge has excellent spatial complexity and requires only a constant level of additional storage space.

Merge and Merge Multiple Ordered Chain Lists

The disadvantage of direct merging is obvious in terms of time cost, that is, only two chains are merged in one cycle. If multiple chains are merged in one cycle, merge and merge, and each time adjacent chains are merged in two, a total of log k cycles are required to merge.

The merge and merge diagram is as follows:

The picture is from LeetCode, Jump Link.

Complete AC Code

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        return merge(lists, 0, lists.length - 1);
    }
	// Divide and Conquer
    public ListNode merge(ListNode[] lists, int l, int r){
        if(l == r) return lists[l];
        if(l > r) return null;
        int mid = (l + r) / 2;
        return mergeList(merge(lists, l, mid), merge(lists, mid + 1,r));
    }

	// Merge two ordered chains
    public ListNode mergeList(ListNode list1, ListNode list2){
        ListNode head = new ListNode();
        ListNode last = head;
        while(list1 != null && list2 != null){
            if(list1.val <= list2.val){
                last.next = list1;
                list1 = list1.next;
            }else{
                last.next = list2;
                list2 = list2.next;
            }
            last = last.next;
        }
        if(list1 != null) last.next = list1;
        if(list2 != null) last.next = list2;
        return head.next;
    }
}

Complexity analysis

Time complexity: O (log k) × K n) still sets the maximum length of each chain table to n, the first merge requires merging k/2 sets of chains, then the time complexity of each combination is O(2n), and the second group merges k/4 sets of chains, and the time complexity of each combination is O(4n). Therefore, the time complexity of each merge is O(k n), so the total time complexity is O(log k). × kn).
Spatial complexity: O(log k), where k is the total number of lists in the array, since recursive calls use stack space.