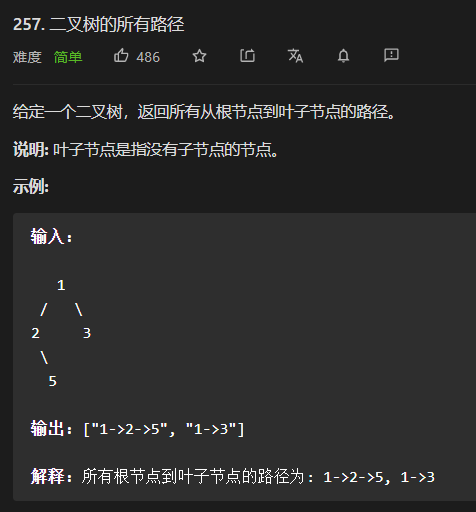
257. All paths of binary tree
Problem description
Idea:
This problem requires the path from the root node to the leaf, so it needs to be traversed in sequence, so that the parent node can point to the child node and find the corresponding path.
We need to go back to another path, so we need to go back one by one.
1. Recursion
① Recursive function parameters and return values
To pass in the root node, record the path of each path and the result of storing the result set. Here recursion does not need to return a value. The code is as follows:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
② Determine recursive termination conditions
Because this problem needs to find the leaf node, that is, when cur is not empty and its left and right children are empty, find the leaf node.
Therefore, the termination condition of this question is:
if (cur->left == NULL && cur->right == NULL) {
//Next, write the logic that handles the termination
}
Here, the path of the vector structure is used to record the path, so the path of the vector structure should be converted to string format and put this string into the result.
The reason for using vector here is that when dealing with single-layer recursive logic, it is necessary to backtrack. Vector is convenient for backtracking.
Therefore, the processing termination logic of this question is:
if (cur->left == NULL && cur->right == NULL) { // Leaf node encountered
string sPath;
for (int i = 0; i < path.size() - 1; i++) { // Convert the path recorded in the path to string format
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]); // Record the last node (leaf node)
result.push_back(sPath); // Collect a path
return;
}
③ Determine single-layer recursive logic
Because it is a preorder traversal, we need to deal with the intermediate node first. The intermediate node is the node on the path we want to record and put it into the path first.
path.push_back(cur->val);
Then there is the process of recursion and backtracking. As mentioned above, it is not judged whether cur is empty. If cur is empty, the next level of recursion will not be carried out.
Therefore, a judgment statement should be added before recursion. Whether the node to be recursed is empty is as follows
if (cur->left) {
traversal(cur->left, path, result);
}
if (cur->right) {
traversal(cur->right, path, result);
}
At this time, it's not finished. After recursion, backtracking should be done, because path can't always add nodes. It also needs to delete nodes before adding new nodes.
So how do you go back? Some students will write as follows:
if (cur->left) {
traversal(cur->left, path, result);
}
if (cur->right) {
traversal(cur->right, path, result);
}
path.pop_back();
This backtracking is a big problem. We know that backtracking and recursion correspond one-to-one. If there is a recursion, there must be a backtracking. In this way, it is equivalent to separating recursion and backtracking, one in curly braces and one outside curly braces.
It should be like this:
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back(); // to flash back
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back(); // to flash back
}
Then the overall code of this question is as follows:
class Solution {
private:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
path.push_back(cur->val);
// This is the leaf node
if (cur->left == NULL && cur->right == NULL) {
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back(); // to flash back
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back(); // to flash back
}
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
vector<int> path;
if (root == NULL)
return result;
traversal(root, path, result);
return result;
}
};
The C + + code above fully reflects backtracking.
Then the above code can be reduced to the following code:
class Solution {
private:
void traversal(TreeNode* cur, string path, vector<string>& result) {
path += to_string(cur->val); // in
if (cur->left == NULL && cur->right == NULL) {
result.push_back(path);
return;
}
if (cur->left)
traversal(cur->left, path + "->", result); // Left
if (cur->right)
traversal(cur->right, path + "->", result); // right
}
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
string path;
if (root == NULL)
return result;
traversal(root, path, result);
return result;
}
};
As mentioned above, the code has been streamlined and many things have been hidden.
Note that when defining the function, void traversal (treenode * cur, string path, vector < string > & result) defines the string path, which is copied and assigned every time. There is no need to use reference, otherwise the effect of backtracking cannot be achieved.
The logic of backtracking is hidden in traversal (cur - > left, path + "- >", result); Path + "- >" in. After each function call, the path is still not added with "- >", which is backtracking.
The second recursive code is concise, but it hides many important points in the code details.
Although the first recursive writing method has more code, it shows every logical processing completely.
2. Iteration
The iterative method of preorder traversal is used to simulate the process of traversing the path.
In addition to simulating recursion, we need a stack to store the corresponding traversal path.
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
stack<TreeNode*> treeSt;// Save traversal nodes of the tree
stack<string> pathSt; // Save nodes traversing the path
vector<string> result; // Save final path collection
if (root == NULL) return result;
treeSt.push(root);
pathSt.push(to_string(root->val));
while (!treeSt.empty()) {
TreeNode* node = treeSt.top(); treeSt.pop(); // Remove from node
string path = pathSt.top();pathSt.pop(); // Take out the path corresponding to the node
if (node->left == NULL && node->right == NULL) { // Leaf node encountered
result.push_back(path);
}
if (node->right) { // right
treeSt.push(node->right);
pathSt.push(path + "->" + to_string(node->right->val));
}
if (node->left) { // Left
treeSt.push(node->left);
pathSt.push(path + "->" + to_string(node->left->val));
}
}
return result;
}
};
In java, you can directly define a stack whose member variable is object stack = new stack < > ();
In this way, you don't need to define two stacks. You can put them in one stack.