The longest ascending subsequence of leetcode 300

Source: LeetCode
Link: https://leetcode-cn.com/problems/long-increasing-subsequence

Blogger Github: https://github.com/GDUT-Rp/LeetCode

Title:

Given an unordered array of integers, find the length of the longest ascending subsequence. c

Example 1:

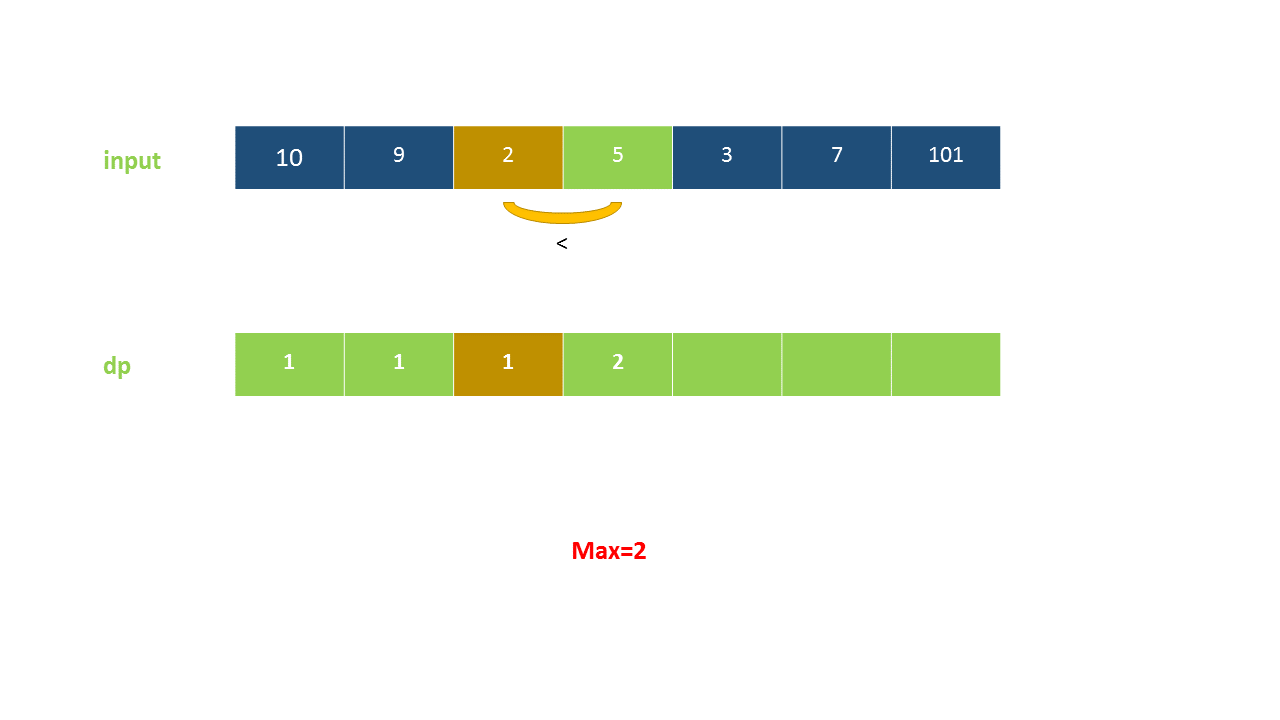
Input: [10,9,2,5,3,7101,18]
Output: 4 
Explanation: the longest ascending subsequence is [2,3,7101], and its length is 4.

Explain:

• There may be multiple combinations of the longest ascending subsequences. You only need to output the corresponding length.
• The time complexity of your algorithm should be O(n2n^2n2).

Solutions:

Method 1: recursion with memory

Intuitive thinking

In the previous method, many recursive calls must use the same parameters to make one call after another. This redundancy can be eliminated by storing the results obtained for a specific call in the two-dimensional memory array memo. memo[i][j]memo[i][j]memo[i][j] indicates the possible length of lis using nums[i]nums[i]nums[i] as the last element considered to be included / not included in lis, where nums[j]nums[j]nums[j] is currently considered to be included / not included in lis. Here, numsnumsnums represents the given array.

C++

class Solution {
public:
    int lengthOfLIS(vector<int> &nums) {
        int len = nums.size();
        
    }
};

Java

public class Solution {
    public int lengthOfLIS(int[] nums) {
        int memo[][] = new int[nums.length + 1][nums.length];
        for (int[] l : memo) {
            Arrays.fill(l, -1);
        }
        return lengthofLIS(nums, -1, 0, memo);
    }
    public int lengthofLIS(int[] nums, int previndex, int curpos, int[][] memo) {
        if (curpos == nums.length) {
            return 0;
        }
        if (memo[previndex + 1][curpos] >= 0) {
            return memo[previndex + 1][curpos];
        }
        int taken = 0;
        if (previndex < 0 || nums[curpos] > nums[previndex]) {
            taken = 1 + lengthofLIS(nums, curpos, curpos + 1, memo);
        }

        int nottaken = lengthofLIS(nums, previndex, curpos + 1, memo);
        memo[previndex + 1][curpos] = Math.max(taken, nottaken);
        return memo[previndex + 1][curpos];
    }
}

Python

class Solution:
    def nthUglyNumber(self, n: int) -> int:
        

Complexity analysis

Time complexity: O(n2)O(n^2)O(n2). The size of the recursive tree can reach n2n^2n2.
Spatial complexity: O (N2) O (N2) O (N2) O (N2), using the mememomemo array of n * nn*nn * n.

Method 2: dynamic planning

His method relies on the fact that the longest ascending subsequence in a given array may reach ithi^{th}ith
Independent of the elements that appear later in the array. Therefore, if we know that the length of lis does not exceed I th I ^ {th} ith, we can calculate the length of lis according to the elements with index j J j including (i+1)th(i+1)^{th}(i+1)th elements, where 0 ≤ j ≤ (i+1) 0 \ Leq j \ Leq (i+1) 0 ≤ j ≤ (i+1).

We use the dpdpdp array to store the required data. dp[i]dp[i]dp[i] indicates the length of the longest possible ascending subsequence considering the array elements up to I th ^ {th} ith, which must include the ith ^ {th} ith element. In order to find dp[i]dp[i]dp[i], we need to try to add the current element (nums[i])(nums[i])(nums[i]) to (i-1)th(i-1)^{th}(i-1)th (including (i-1)th {th} (i-1)th) in each possible longest ascending subsequence, so that the new sequence formed by adding the current element is also an ascending subsequence. Therefore, it is easy to determine that dp[i]dp[i]dp[i] uses:
dp[i]=max(dp[j])+1,∀0≤j<i dp[i] = \text{max}(dp[j]) + 1, \forall 0\leq j < i dp[i]=max(dp[j])+1,∀0≤j<i
Finally, the maximum of all dp[i]dp[i]dp[i] of the final result is determined.

LISlength=max(dp[i]),∀0≤i<n LIS_{length}= \text{max}(dp[i]), \forall 0\leq i < n LISlength​=max(dp[i]),∀0≤i<n

C++

class Solution {
public:
    int lengthOfLIS(vector<int> &nums) {
        int len = nums.size();
        if (len == 0) return 0;
        vector<int> dp(len, 1);
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < len; ++i) {
            int maxval = 0;
            for (int j = 0; j < i; ++j) {
                if (nums[i] > nums[j]) {
                    maxval = max(maxval, dp[j]);
                }
            }
            dp[i] = maxval + 1;
            maxans = max(maxans, dp[i]);
        }
        return maxans;
    }
};

Java

public class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        dp[0] = 1;
        int maxans = 1;
        for (int i = 1; i < dp.length; i++) {
            int maxval = 0;
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    maxval = Math.max(maxval, dp[j]);
                }
            }
            dp[i] = maxval + 1;
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}

Python

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        

Complexity analysis

• Time complexity: O(n2)O(n^2)O(n2). There are two cycles of nnn.
• Space complexity: O(n)O(n)O(n), using the matrix dpdpdp with the size of nnn.