LeetCode 84: the largest rectangle in the histogram
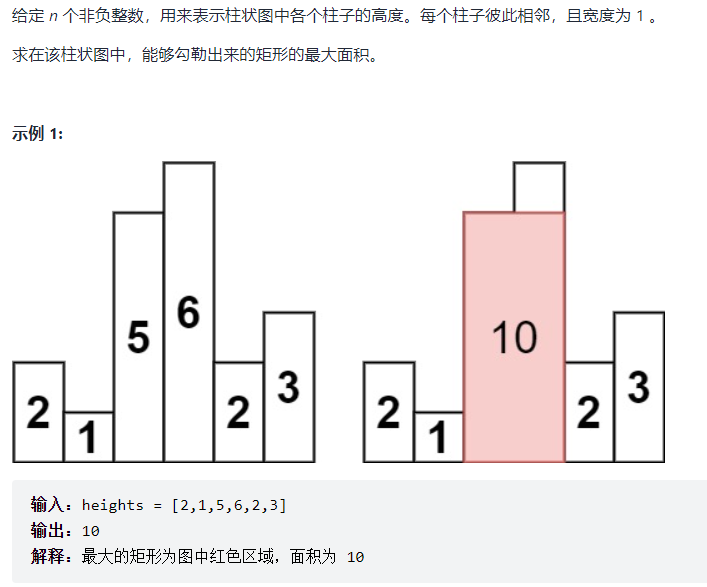

answer
These two monotonous problems need to be reflected. Why are the ideas generally correct but have not been done
Code one
The first mock exam is to imitate the double pointer in rain water.
- In the rain water, find the highest column on the left and right sides of val, and take min to get the height of the horizontal plane
- In this question, we want to find the column index that Val expands from left to right, and is greater than or equal to Val to the left / right as far as possible. This is the calculated width and the height is val
It seems that it is based on val to find wide constraints. I came up with this idea myself, but I didn't write code, because the worst-case complexity is O(n^2),
However, the complexity of the following code should be slightly higher than O(n). The complexity of the while part is not easy to analyze. When using the combination of search set records and space for time, when heights[t] > = heights[i], the heights[t] is higher than the heights[i]. The first column on the left of the heights[t] that is smaller than the column minLeftIndex[t], may be higher than the heights[i], and may be lower than the heights[i],
- If it is lower than heights[i], there are no columns lower than heights[t] in the interval from minLeftIndex[t] to heights[i], but all columns higher than heights[t] (heights[t] > = heights[i]), so minLeftIndex[i] = t;
- If it is higher than heights[i], repeat the above process

class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
vector<int> minLeftIndex(heights.size());
vector<int> minRightIndex(heights.size());
int size = heights.size();
// Record the first subscript on the left of each column that is smaller than the column
minLeftIndex[0] = -1; // Note the initialization here to prevent the following while loop
for (int i = 1; i < size; i++) {
int t = i - 1;
// This is not if, but the process of constantly looking to the left
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// Record the first subscript on the right of each column that is smaller than the column
minRightIndex[size - 1] = size; // Note the initialization here to prevent the following while loop
for (int i = size - 2; i >= 0; i--) {
int t = i + 1;
// This is not if, but the process of constantly looking to the right
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// Sum
int result = 0;
for (int i = 0; i < size; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
}
return result;
}
};
Code two
My first thought was to find the column index greater than or equal to val to the left / right as much as possible, because I wanted to expand to the left and right as much as possible.
But consider monotonically decreasing stack (decreasing from top to bottom), such as 1, 3, 5, The next element (from the top of the stack to the bottom of the stack) is the first one on the left less than the element (when entering the stack, the first number on the right of the element on the top of the stack that is larger than itself is the current element, similarly, the first number on the left of the current element that is smaller than itself is the top of the stack, and then the current element enters the stack). In fact, it is to find the first element smaller than itself for each number in a one-dimensional array. It is not appropriate to use columns greater than or equal to val.
Consider a monotonically decreasing stack, such as 1, 3 and 2. When 1 and 3 enter the stack and 2 wants to enter the stack, for 3, the first element less than 3 on the left is 1, and the first element less than 3 on the right is 2 and 3. The left and right boundaries are found.
For example, 1, 2 and 3, when 1 and 2 are stacked and 3 is stacked, for 2, the first element on the left less than 2 is 1, and the first element on the right less than 2 is unknown (because 3 can be directly stacked).
That is, the maximum rectangle of the stack element column can be calculated at present
The core is the purpose of monotone stack:
Find the first element larger / smaller than yourself on the left / right
Take the example above and write it clearly
From left to right, decrease from the top of the stack to the bottom of the stack: 1, 3, 5, 4, 2. Find the first element on the left / right that is smaller than yourself. Note that when now=4, 5 will exit the stack. The left is 3 in the stack and the right is now=4. Note that the first element on the left is 3 smaller than yourself, and the first element on the right is 4 smaller than yourself
From left to right, increase from the top of the stack to the bottom of the stack: 5, 3, 1, 2, 4. Find the first element on the left / right that is larger than yourself
// my solution
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
int now=0, left=0, right=0, mid=0, ans=0;
for(int i=0; i<heights.size(); i++){
now = heights[i];
if(st.empty()) st.push(i);
else if(now > heights[st.top()]) st.push(i);
else if(now == heights[st.top()]) {// Because it is the first element index less than val on the left
st.pop();
st.push(i);
}
else{ // Now < heights [st.top()], for example: 1, 3, 2
while(!st.empty() && now < heights[st.top()]){
mid = st.top();
st.pop();
if(st.empty()) { // heights[mid] not on the left
ans = max(ans, (i-0)*heights[mid]);
break;
}
right = i;
left = st.top();
ans = max(ans, (right-left-1)*heights[mid]);
}
st.push(i);
}
}
right = heights.size();
while(!st.empty()){
mid = st.top();
st.pop();
if(st.empty()){
ans = max(ans, (int)(heights[mid] * heights.size() ));
break;
}
left = st.top();
ans = max(ans, (right-left-1)*heights[mid]);
// right = left;
}
return ans;
}
};
Code three
Similar to code 1, it also looks for the first column smaller than the element from left to right, and uses the monotonic decreasing stack described above (decreasing from the top of the stack to the bottom of the stack)
Use the decrement stack from left to right to find the first value less than the element on the left of each element, and use the decrement stack from right to left to find the first value less than the element on the right of each element
Each element can be put on the stack and out of the stack at most once, so the complexity is O(n)
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int n = heights.size();
vector<int> left(n), right(n);
stack<int> mono_stack;
for (int i = 0; i < n; ++i) {
while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {
mono_stack.pop();
}
left[i] = (mono_stack.empty() ? -1 : mono_stack.top());
mono_stack.push(i);
}
mono_stack = stack<int>();
for (int i = n - 1; i >= 0; --i) {
while (!mono_stack.empty() && heights[mono_stack.top()] >= heights[i]) {
mono_stack.pop();
}
right[i] = (mono_stack.empty() ? n : mono_stack.top());
mono_stack.push(i);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans = max(ans, (right[i] - left[i] - 1) * heights[i]);
}
return ans;
}
};
Summary
The core problem is to find the first index on the left and right that is less than the element (note that it is not greater than or equal to). After being familiar with the monotone stack, you should naturally think of the idea of code 3 and traverse it twice from left to right and right to left
The idea of code 2 is that after traversing from left to right, the first index on the left and right of each element can be determined at the same time. (eg: from left to right, decreasing from the top of the stack to the bottom of the stack: 1, 3, 5, 4, 2),