978 · basic calculator
Implement a basic calculator to calculate a simple expression.
The expression string may contain left parenthesis' ('and right parenthesis'), plus sign' + 'or minus sign' - ', non negative integer and space'.
The expression given is always reasonable.

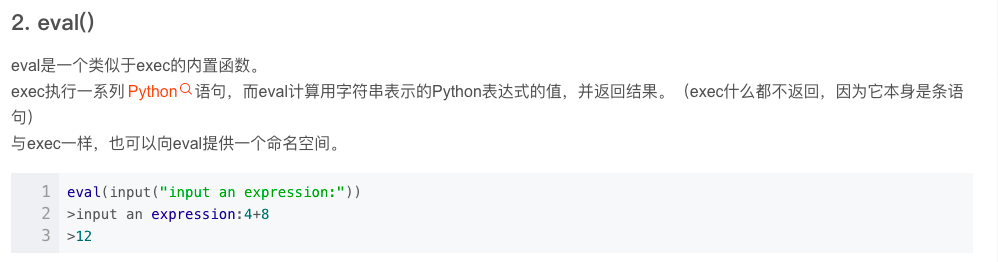
Learned the usage of eval.
An error was encountered:
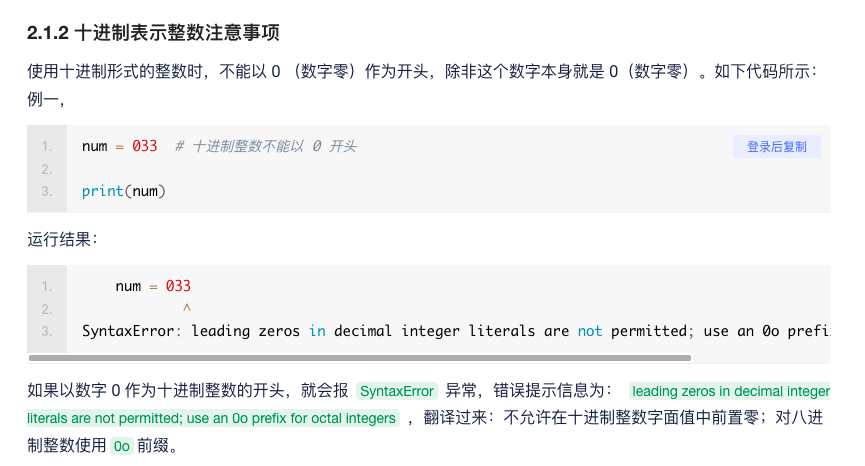
Everything else is OK. This decimal system cannot start with 0 and will not be solved. Learned a new method eval, very easy to use.
class Solution:
"""
@param s: the given expression
@return: the result of expression
"""
def calculate(self, s):
# Write your code here
stack = []
li = []
for ch in s:
if ch != ')':
stack.append(ch)
else:
while stack[-1] != '(':
li.append(stack.pop())
stack.pop()
# Calculate li
li.reverse()
stack.append(str(eval(''.join(li))))
li = []
return eval(''.join(stack))
I read an answer, which is easier to understand. Learned about the use of number and sign.
def calculate(self, s):
# Write your code here
stack = []
number = 0
for ch in s:
if ch == '(':
stack.append(ch)
elif ch.isdigit():
number = number * 10 + int(ch)
elif ch == '+' or ch == '-':
stack.append(number)
stack.append(ch)
number = 0
elif ch == ')':
stack.append(number)
strs = []
while stack and stack[-1] != '(':
strs.append(stack.pop())
strs.reverse()
result = self.helper(strs)
if stack[-1] == '(':
stack.pop()
stack.append(result)
number = 0
stack.append(number)
output = self.helper(stack)
return output
def helper(self, strs):
result = 0
sign = 1
for element in strs:
if isinstance(element, int):
result += sign * element
elif element == '+':
sign = 1
elif element == '-':
sign = -1
return result
227. Simulation of Hanoi Tower problem with stack
In the classical Hanoi Tower problem, there are three towers and N plates of different sizes, and the plates can be moved to any tower. It is required that the plates must be stacked from top to bottom in the order from small to large (for example, any plate must be stacked on a plate larger than it). At the same time, you must meet the following restrictions:
(1) Only one plate can be moved at a time.
(2) Only the plates at the top of the tower can be moved.
(3) Each plate can only be placed on a plate larger than it.
Please write a program to move the plate of the first tower to the last tower.

can't
class Tower:
"""
@param: i: An integer from 0 to 2
"""
def __init__(self, i):
# create three towers
self.disks = []
"""
@param: d: An integer
@return: nothing
"""
def add(self, d):
# Add a disk into this tower
if len(self.disks) > 0 and self.disks[-1] <= d:
print("Error placing disk %s" % d)
else:
self.disks.append(d)
"""
@param: t: a tower
@return: nothing
"""
def moveTopTo(self, t):
# Move the top disk of this tower to the top of t.
t.disks.append(self.disks.pop())
"""
@param: n: An integer
@param: destination: a tower
@param: buffer: a tower
@return: nothing
"""
def move_disks(self, n, destination, buffer):
# Move n Disks from this tower to destination by buffer tower
for i in range(n):
buffer.disks.append(self.moveTopTo(buffer))
for i in range(n):
destination.disks.append(self.moveTopTo(destination))
"""
@return: Disks
"""
def getDisks(self):
# write your code here
return self.disks
"""
Your Tower object will be instantiated and called as such:
towers = [Tower(0), Tower(1), Tower(2)]
for i in xrange(n - 1, -1, -1): towers[0].add(i)
towers[0].move_disks(n, towers[2], towers[1])
print towers[0], towers[1], towers[2]
"""
The answer is recursive:
class Tower(object):
# create three towers (i from 0 to 2)
def __init__(self, i):
self.disks = []
# Add a disk into this tower
def add(self, d):
if len(self.disks) > 0 and self.disks[-1] <= d:
print("Error placing disk %s")
else:
self.disks.append(d);
# @param {Tower} t a tower
# Move the top disk of this tower to the top of t.
def move_top_to(self, t):
# Write your code here
t.add(self.disks.pop())
# @param {int} n an integer
# @param {Tower} destination a tower
# @param {Tower} buffer a tower
# Move n Disks from this tower to destination by buffer tower
def move_disks(self, n, destination, buffer):
# Write your code here
if n > 0:
self.move_disks(n - 1, buffer, destination)
self.move_top_to(destination)
buffer.move_disks(n - 1, destination, self)
def get_disks(self):
return self.disks
"""
Your Tower object will be instantiated and called as such:
towers = [Tower(0), Tower(1), Tower(2)]
for i in xrange(n - 1, -1, -1): towers[0].add(i)
towers[0].move_disks(n, towers[2], towers[1])
print towers[0], towers[1], towers[2]
"""
In this code, I'm still a little confused about self here:
def move_disks(self, n, destination, buffer):
# Write your code here
if n > 0:
self.move_disks(n - 1, buffer, destination)
self.move_top_to(destination)
buffer.move_disks(n - 1, destination, self)
264. Number of general subarrays
Give an array of 2 or 4. If the subarray of an array (subarray is a group of adjacent elements in the array and cannot be empty) meets the following conditions, it is called "general":
- 2 and 4 are grouped consecutively (e.g. [4, 2], [2, 4], [4, 4, 2, 2], [2, 2, 4, 4], [4, 4, 2, 2, 2], etc.).
- The number of 4 in the subarray is equal to the number of 2 in the subarray.
- Subarrays with the same elements but different positions are regarded as different. For example, there are two [4,2] subarrays in the array [4,2,4,2].
You need to return an integer value, that is, the number of "general" subarrays in a given array.

No, just look at the answer:

class Solution:
"""
@param array: An given array.
@return: Return the number of "universal" subarrays.
"""
def subarrays(self, array):
size = len(array)
# Record the current number of consecutive 2 and 4
count_2 = 0
count_4 = 0
# An array of 2 or 4 consecutive numbers
queue = []
for i in range(size):
if array[i] == 4:
if i > 0 and array[i-1] == 2:
queue.append(count_2)
count_2 = 0
count_4 += 1
if array[i] == 2:
if i > 0 and array[i-1] == 4:
queue.append(count_4)
count_4 = 0
count_2 += 1
# 2 or 4 consecutive processing
if array[size-1] == 4:
queue.append(count_4)
else:
queue.append(count_2)
# Two adjacent numbers are added to the result in min
result = 0
for i in range(1, len(queue)):
result += min(queue[i], queue[i-1])
return result