1. Title
Given the root node root and a value key of a binary search tree, delete the node corresponding to the key in the binary search tree and ensure that the nature of the binary search tree remains unchanged. Returns a reference to the root node of a binary search tree that may be updated.
Generally speaking, deleting a node can be divided into two steps:
- First, find the node to be deleted;
- If found, delete it.
1.1 example
- Example 1 1 1 :
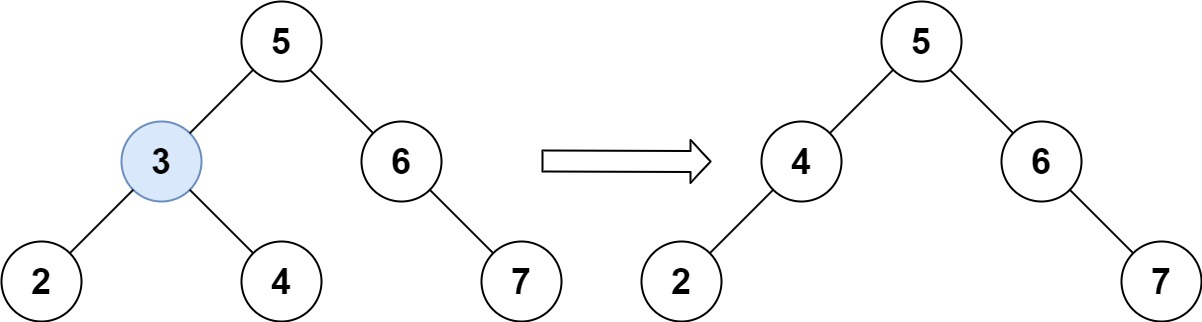
- Input: root = [5, 3, 6, 2, 4, null, 7], key = 3;
- Output: [5, 4, 6, 2, null, null, 7];
- Explanation: the given value of the node to be deleted is
3
3
3, so we found it first
3
3
3 this node, and then delete it. A correct answer is [5, 4, 6, 2, null, null, 7], as shown in the figure below. Another correct answer is [5, 2, 6, null, 4, null, 7].
- Example 2 2 2 :
- Input: root = [5, 3, 6, 2, 4, null, 7], key = 0;
- Output: [5, 3, 6, 2, 4, null, 7];
- Explanation: the binary tree does not contain a value of 0 0 Node for 0.
1.2 description
- Source: LeetCode
- Link: https://leetcode-cn.com/problems/delete-node-in-a-bst
1.3 restrictions
- Node value is unique;
- Range of nodes [ 0 , 1 0 4 ] [0, 10^4] [0,104] ;
- − 1 0 5 < = key < = 1 0 5 -10^5 <= \text{key} <= 10^5 −105<=key<=105 ;
- − 1 0 5 < = Node.val < = 1 0 5 -10^5 <= \text{Node.val} <= 10^5 −105<=Node.val<=105 ;
- Root is the root node of the legal binary search tree.
1.4 advanced
The time complexity of the algorithm is required to be O ( h ) O(h) O(h) , h h h is the height of the tree.
2. Solution I
- Author: GeeksforGeeks
2.1 analysis
When deleting a node of the binary search tree, the first step is naturally to find the target node. This step is very simple. It is easy to know in combination with the nature of the binary search tree. If the current node is node, then:
- When node.val > k, the target node is in the left subtree of node;
- When node. Val < K, the target node is in the right subtree of node;
- When node.val == k, delete the target node.
The difficulty of this problem is not to find the target node to be deleted, but how to delete the target node, because it is necessary to ensure that after deleting the target node, the result is still a binary search tree, which can be discussed in three cases:
- If the target node is a leaf node, delete the target node directly:
50 50
/ \ delete(20) / \
30 70 ---------> 30 70
/ \ / \ \ / \
20 40 60 80 40 60 80
- The target node has only one child node. Just overwrite the val of the target node with the val of the child node, and then delete the child node:
50 50
/ \ delete(30) / \
30 70 ---------> 40 70
\ / \ / \
40 60 80 60 80
- The target node has two child nodes. At this time, you need to find the successor node of the target node, then overwrite the val of the target node with the val of the successor node, and finally delete the successor node 1 You can:
50 60
/ \ delete(50) / \
40 70 ---------> 40 70
/ \ \
60 80 80
It should be noted that only when the right child node of the target node is not empty, the successor node of the target node is required. A protected method is defined here_ min_node to find the successor node of the target node, that is, the successor node is regarded as the node with the smallest val of the right child node (subtree) of the target node.
2.2 realization
from typing import Optional, List
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def inorder(self, root: TreeNode) -> List[int]:
if not isinstance(root, TreeNode):
return []
return self.inorder(root.left) + [root.val] + self.inorder(root.right)
def _min_node(self, node):
cursor = node
# loop down to find the leftmost leaf
while cursor.left is not None:
cursor = cursor.left
return cursor
def delete_node(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
if not isinstance(root, TreeNode):
return
# If the key to be deleted is smaller than the root's key then it lies in the left subtree
if key < root.val:
root.left = self.delete_node(root.left, key)
# If the key to be deleted is greater than the root's key then it lies in the right subtree
elif key > root.val:
root.right = self.delete_node(root.right, key)
# If key is the same as root's key, then this is the node to be deleted
else:
# Node with only one child or no child
if root.left is None:
child = root.right
return child
elif root.right is None:
child = root.left
return child
# Node with two children: Get the inorder successor (smallest in the right subtree)
successor = self._min_node(root.right)
# Copy the inorder successor's val attribute to this node
root.val = successor.val
# Delete the inorder successor
root.right = self.delete_node(root.right, successor.val)
return root
def main():
node7 = TreeNode(80)
node6 = TreeNode(60)
node5 = TreeNode(40)
node4 = TreeNode(20)
node3 = TreeNode(70, left=node6, right=node7)
node2 = TreeNode(30, left=node4, right=node5)
node1 = TreeNode(50, left=node2, right=node3)
root = node1
sln = Solution()
print('inorder:', sln.inorder(root)) # inorder: [20, 30, 40, 50, 60, 70, 80]
sln.delete_node(root, 20)
print('inorder:', sln.inorder(root)) # inorder: [30, 40, 50, 60, 70, 80]
sln.delete_node(root, 30)
print('inorder:', sln.inorder(root)) # inorder: [40, 50, 60, 70, 80]
sln.delete_node(root, 50)
print('inorder:', sln.inorder(root)) # inorder: [40, 60, 70, 80]
sln.delete_node(root, 90)
print('inorder:', sln.inorder(root)) # inorder: [40, 60, 70, 80]
if __name__ == '__main__':
main()
2.3 complexity
- Time complexity: O ( n ) O(n) O(n), in the worst case, the binary search tree is chain. At this time, if the leaf node is deleted, each node will be traversed;
- Space complexity: O ( n ) O(n) O(n), in the worst case, the binary search tree is chain, and the depth of recursive call is O ( n ) O(n) O(n), that is, the implicit overhead of maintaining recursion is positively correlated with depth.
Precursor nodes can also be used here. ↩︎