catalogue
Question 1: continuous subarrays and
Question 3: intersecting linked list
Question 4: goals and objectives
Question 5: weight of the last stone II
Question 6: constructing rectangles
Question 9: different paths II
Leetcode brushes questions regularly, with 10 questions in each issue. Comrades with heavy business can see the ideas I share. It is not the most efficient solution, but only for mutual improvement.
Question 1: Continuous subarrays and
The requirements of the test questions are as follows:

Answer (C language):
struct HashTable {
int key, val;
UT_hash_handle hh;
};
bool checkSubarraySum(int* nums, int numsSize, int k) {
int m = numsSize;
if (m < 2) {
return false;
}
struct HashTable* hashTable = NULL;
struct HashTable* tmp = malloc(sizeof(struct HashTable));
tmp->key = 0, tmp->val = -1;
HASH_ADD_INT(hashTable, key, tmp);
int remainder = 0;
for (int i = 0; i < m; i++) {
remainder = (remainder + nums[i]) % k;
HASH_FIND_INT(hashTable, &remainder, tmp);
if (tmp != NULL) {
int prevIndex = tmp->val;
if (i - prevIndex >= 2) {
return true;
}
} else {
tmp = malloc(sizeof(struct HashTable));
tmp->key = remainder, tmp->val = i;
HASH_ADD_INT(hashTable, key, tmp);
}
}
return false;
}The operating efficiency is as follows:

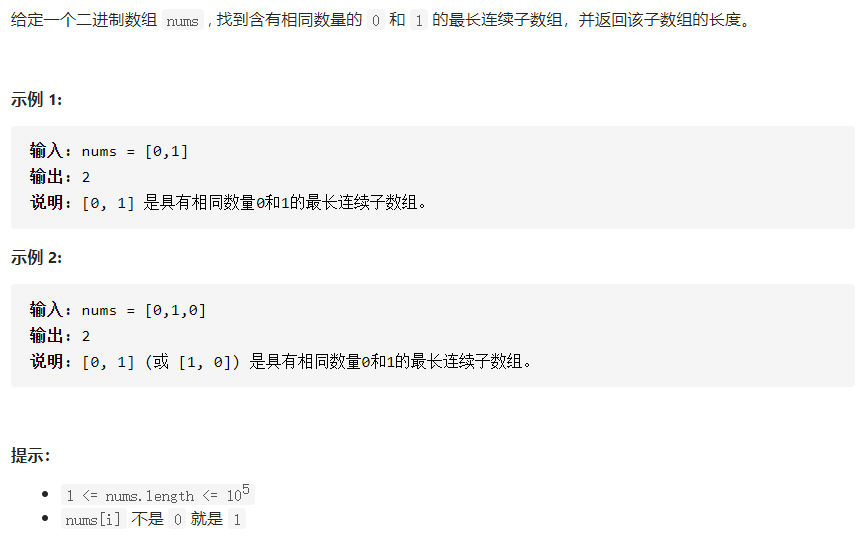
Question 2: Continuous array
The requirements of the test questions are as follows:
Answer (C language):
#include <stdio.h>
int findMaxLength(int* nums, int numsSize){
int *hash = (int *)malloc(sizeof(int) * (numsSize * 2 + 1));
for (int i = 0; i < (numsSize * 2 + 1); i++) {
hash[i] = -2;
}
int maxlen = 0;
int count = 0;
hash[numsSize] = -1;
for (int i = 0; i < numsSize; i++) {
count += nums[i] == 0 ? -1 : 1;
if (hash[count + numsSize] != -2) {
maxlen = fmax(maxlen, i - hash[count+numsSize]);
} else {
hash[count + numsSize] = i;
}
}
free(hash);
return maxlen;
}The operating efficiency is as follows:

Question 3: Intersecting linked list
The requirements of the test questions are as follows:

Answer (C language):
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
struct ListNode *p=headA, *q=headB;
while(p!=q&&(p!=NULL||q!=NULL))
{
if(p==NULL)
p=headB;
else
p=p->next;
if(q==NULL)
q=headA;
else
q=q->next;
}
return p;
}The operating efficiency is as follows:

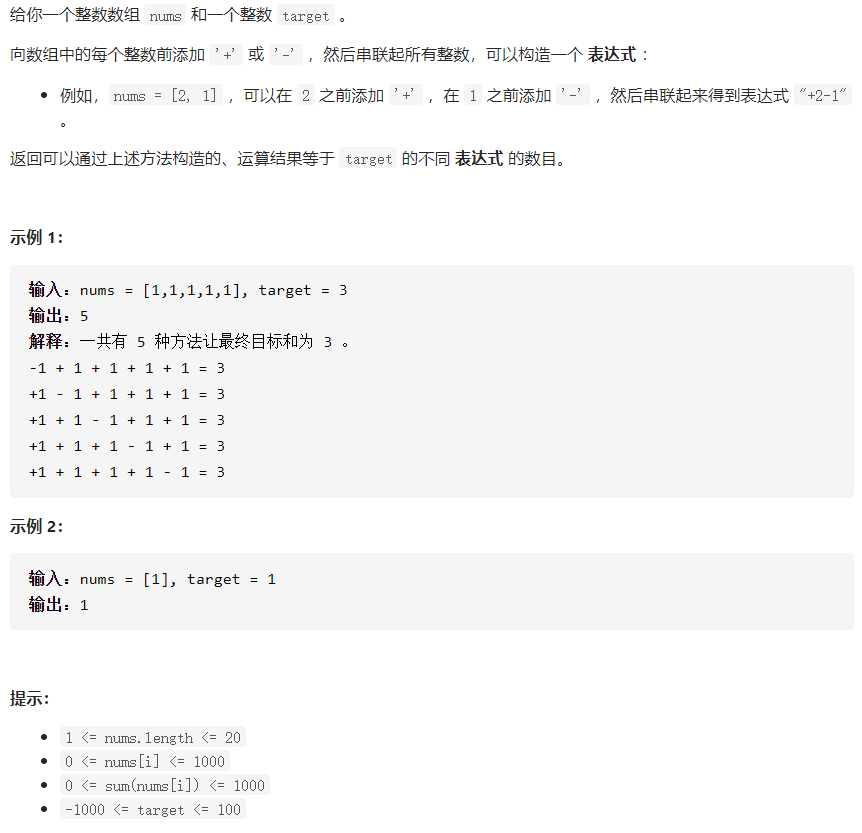
Question 4: Objectives and
The requirements of the test questions are as follows:
Answer (C language):
int findTargetSumWays(int* nums, int numsSize, int target){
int sum = 0;
for (int i = 0; i < numsSize; i++) {
sum += nums[i];
}
if ((sum + target) % 2 != 0) {
return 0;
}
int targetA = (sum + target) / 2;
int *dp = (int *)malloc(sizeof(int) * (targetA + 1));
memset(dp, 0, sizeof(int) * (targetA + 1));
dp[0] = 1;
for (int i = 0; i < numsSize; i++) {
for (int j = targetA; j >= nums[i]; j--) {
dp[j] = dp[j] + dp[j - nums[i]];
}
}
return dp[targetA];
}The operating efficiency is as follows:

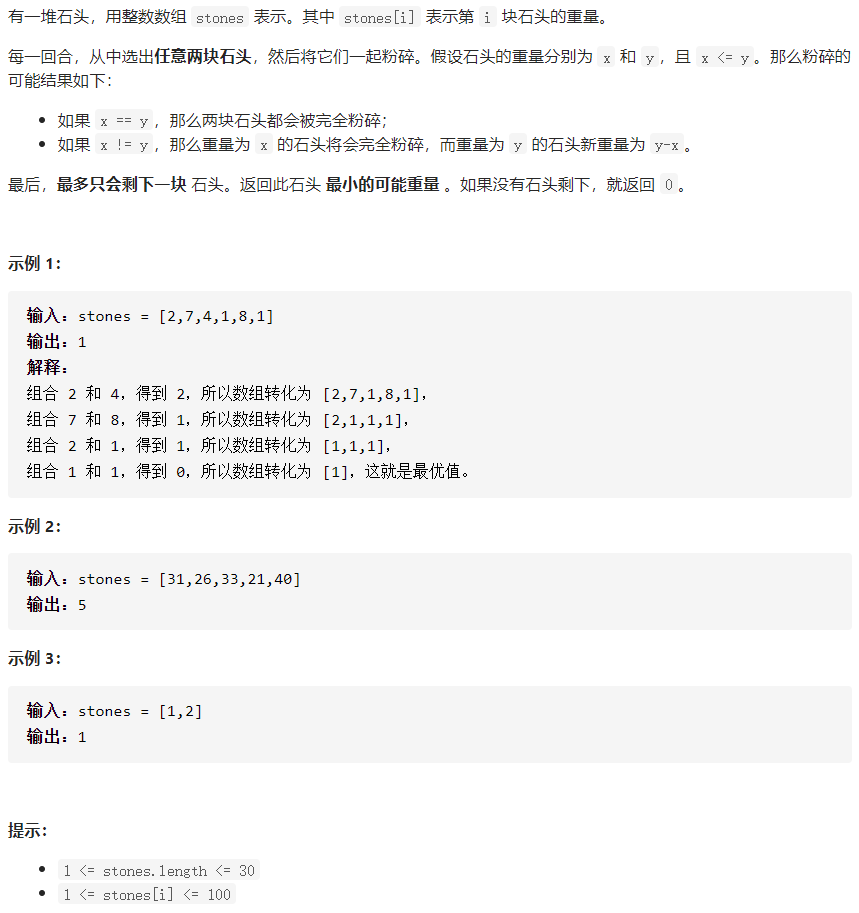
Question 5: Weight of the last stone II
The requirements of the test questions are as follows:
Answer (C language):
int lastStoneWeightII(int* stones, int stonesSize) {
int sum = 0;
for (int i = 0; i < stonesSize; i++) {
sum += stones[i];
}
int n = stonesSize, m = sum / 2;
int dp[n + 1][m + 1];
memset(dp, 0, sizeof(dp));
dp[0][0] = true;
for (int i = 0; i < n; ++i) {
for (int j = 0; j <= m; ++j) {
if (j < stones[i]) {
dp[i + 1][j] = dp[i][j];
} else {
dp[i + 1][j] = dp[i][j] || dp[i][j - stones[i]];
}
}
}
for (int j = m;; --j) {
if (dp[n][j]) {
return sum - 2 * j;
}
}
}The operating efficiency is as follows:

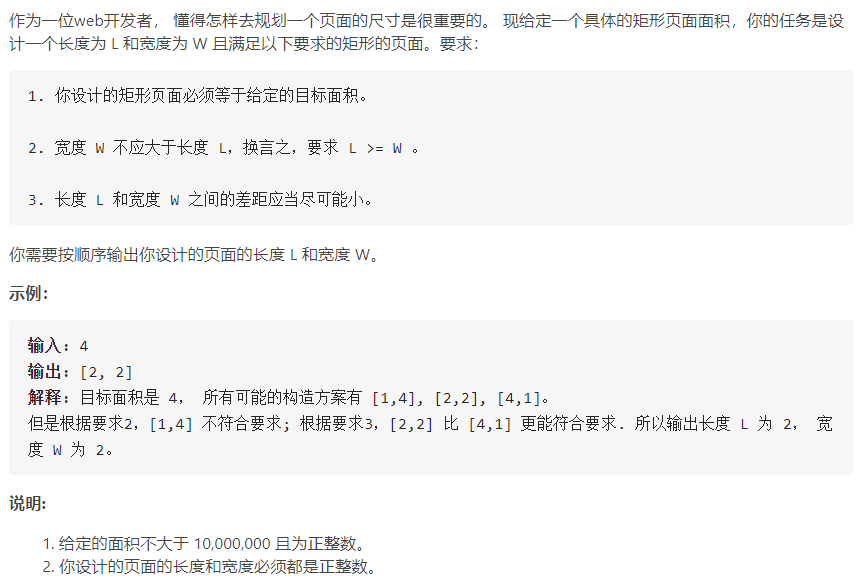
Question 6: Construct rectangle
The requirements of the test questions are as follows:
Problem solving ideas:
The main difficulty of this problem is to find two similar and multiplied by the length and width of the area, so use the square to find the middle number, and then decrease in turn to find the number that can be divided.
Answer (C language):
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* constructRectangle(int area, int* returnSize){
*returnSize=2;
int *a = (int *)malloc(sizeof(int)*2);
int b = (int)sqrt(area);
while(area % b !=0){
b--;
}
a[1]=b;
a[0]=area/b;
return a;
}The operating efficiency is as follows:

Question 7: Change II
The requirements of the test questions are as follows:

Answer (C language):
int change(int amount, int* coins, int coinsSize) {
int dp[amount + 1];
memset(dp, 0, sizeof(dp));
dp[0] = 1;
for (int i = 0; i < coinsSize; i++) {
for (int j = coins[i]; j <= amount; j++) {
dp[j] += dp[j - coins[i]];
}
}
return dp[amount];
}The operating efficiency is as follows:

Question 8: Complete square
The requirements of the test questions are as follows:

Answer (C language):
int numSquares(int n) {
int f[n + 1];
f[0] = 0;
for (int i = 1; i <= n; i++) {
int minn = INT_MAX;
for (int j = 1; j * j <= i; j++) {
minn = fmin(minn, f[i - j * j]);
}
f[i] = minn + 1;
}
return f[n];
}The operating efficiency is as follows:

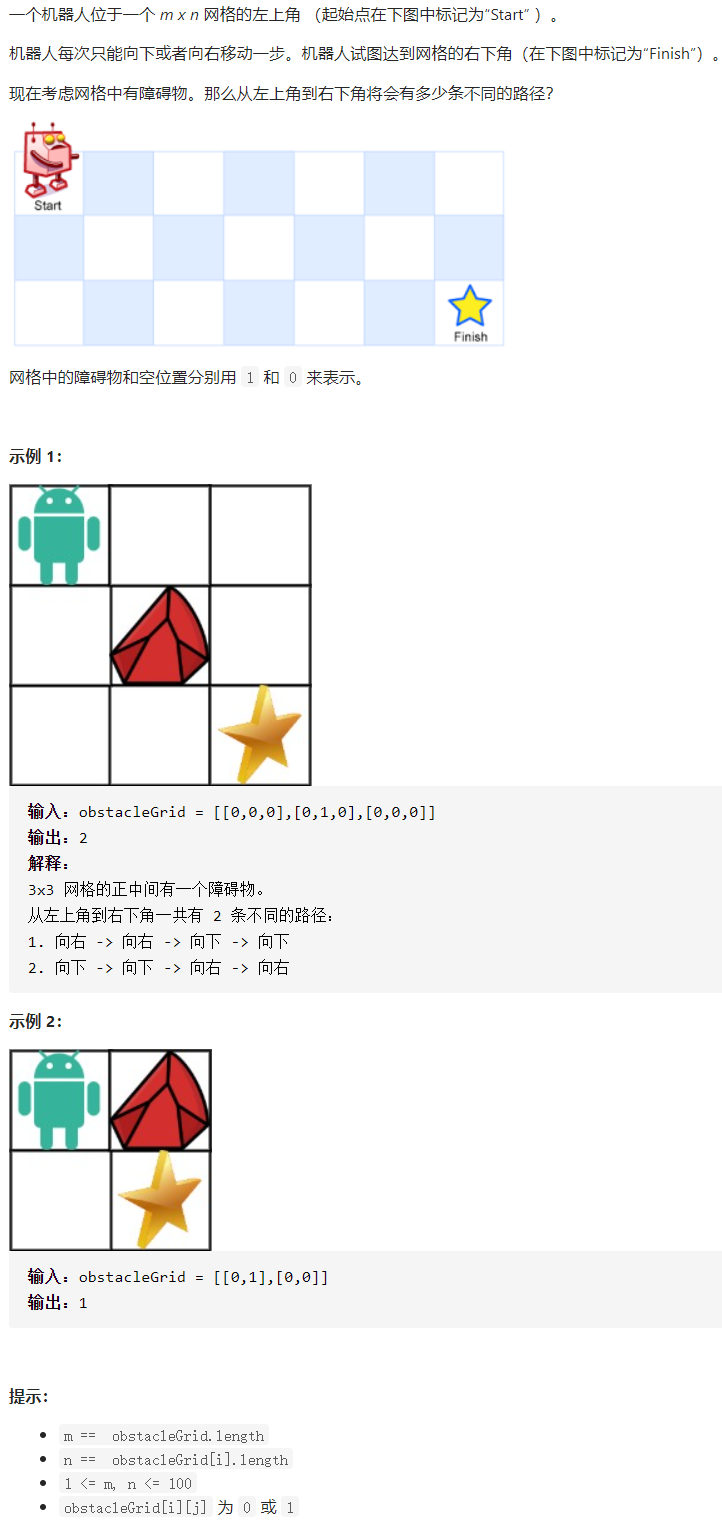
Question 9: Different paths II
The requirements of the test questions are as follows:
Answer (C language):
int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize) {
/* 1,dp Array meaning: the number of paths from (0, 0) to column j of the current row */
int dp[*obstacleGridColSize];
/* 2,State transition equation:
* if (obstacleGrid[i][j] == 1) {
* dp[j] = 0;
* } else {
* dp[j] += dp[j - 1];
* }
*/
/* 3,dp initial value
* In the first row, it is 1 before the roadblock and 0 after the roadblock
*/
if (obstacleGrid[0][0] == 1) {
dp[0] = 0;
} else {
dp[0] = 1;
}
for (int j = 1; j < *obstacleGridColSize; j++) {
if (obstacleGrid[0][j] == 1) {
dp[j] = 0;
} else {
dp[j] = dp[j - 1];
}
}
/* 4,Traversal order: traversal layer by layer from left to right */
for (int i = 1; i < obstacleGridSize; i++) {
for (int j = 0; j < *obstacleGridColSize; j++) {
if (j == 0) { /* start */
if (obstacleGrid[i][j] == 1) {
/* There are roadblocks on the current path: dp is 0 */
dp[j] = 0;
} else {
/* There are no roadblocks on the current path: skip */
continue;
}
} else { /* Non beginning */
if (obstacleGrid[i][j] == 1) {
/* There are roadblocks on the current path: dp is 0 */
dp[j] = 0;
} else {
/* There are no roadblocks on the current path: calculate the number of paths */
dp[j] += dp[j - 1];
}
}
}
}
return dp[*obstacleGridColSize - 1];
}The operating efficiency is as follows:

Question 10: Stone game
The requirements of the test questions are as follows:

Answer (C language):
bool stoneGame(int* piles, int pilesSize) {
int dp[pilesSize][pilesSize];
for (int i = 0; i < pilesSize; i++) {
dp[i][i] = piles[i];
}
for (int i = pilesSize - 2; i >= 0; i--) {
for (int j = i + 1; j < pilesSize; j++) {
dp[i][j] = fmax(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
}
}
return dp[0][pilesSize - 1] > 0;
}The operating efficiency is as follows:
