Title Description

Given an array prices, where   prices[i] is the price of a given stock on day I.

Design an algorithm to calculate the maximum profit you can make. You can complete as many transactions as possible (buying and selling a stock multiple times).

Note: you cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).

Example 1

Input: prices = [7,1,5,3,6,4]
Output: 7
Explanation: if you buy on the second day (stock price = 1) and sell on the third day (stock price = 5), this exchange can make a profit = 5-1 = 4.
     Then, buy on the 4th day (stock price = 3) and sell on the 5th day (stock price = 6). This exchange can make a profit = 6-3 = 3.

Example 2

Input: prices = [1,2,3,4,5]
Output: 4
Explanation: if you buy on the first day (stock price = 1) and sell on the fifth day (stock price = 5), this exchange can make a profit = 5-1 = 4.
     Note that you can't buy stocks on day 1 and day 2 and then sell them. Because you are involved in multiple transactions at the same time, you must sell the previous shares before buying again.

dynamic programming algorithm

Open up a two-dimensional dp array with the same length as the prices array. dp[i][0] represents the maximum profit accumulated by holding stocks on that day, and dp[i][1] represents the maximum profit of holding stocks on that day. If the length of prices is n, it is easy to know that the maximum profit can be obtained when there are no stocks on the last day. Therefore, only dp[n-1][1] is required.

The state transition equation is:

i=0:

                             

                               

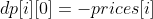
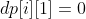
i>0:

                              
                              

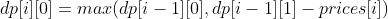
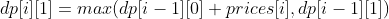
C + + code

#include<iostream>
#include<vector>
using namespace std;
class Solution {
public:
	int maxProfit(vector<int>& prices)
	{
		int** dp = new int* [prices.size()];
		for (int i = 0; i < prices.size(); i++)
		{
			dp[i] = new int[2];
			dp[i][0] = 0; dp[i][1] = 0;
		}
		dp[0][0] = -prices[0];
		dp[0][1] = 0;
		for (int i = 1; i < prices.size(); i++)
		{
			dp[i][0] = dp[i - 1][0] > dp[i - 1][1] - prices[i] ? dp[i - 1][0] : dp[i - 1][1] - prices[i];
			dp[i][1] = dp[i - 1][0] + prices[i] > dp[i - 1][1] ? dp[i - 1][0] + prices[i] : dp[i - 1][1];
		}
		return dp[prices.size() - 1][1];
	}
};
int main() {
	int n=0;
	vector<int>prices;
	while (cin >> n)
	{
		if (n == 0)break;
		prices.push_back(n);
	}
	Solution DP;
	int result = DP.maxProfit(prices);
	cout << result << endl;
}

python code

cin=input()
temp=cin.split(' ')
dp=[]
for i in range(len(temp)):
    dp.append([0,0])
dp[0][0]=-eval(temp[0])
dp[0][1]=0
for i in range(1,len(temp)):
    dp[i][0]=max(dp[i-1][0],dp[i-1][1]-eval(temp[i]))
    dp[i][1]=max(dp[i-1][0]+eval(temp[i]),dp[i-1][1])
    print(dp[i][0],end=' ')
    print(dp[i][1])
print(dp[len(temp)-1][1])

Greedy Algorithm

When the value of the interval increases continuously, the value of the right endpoint minus the value of the left endpoint is greater than the sum of the value of the right endpoint minus the value of the left endpoint of the sub interval;

When the value of the interval does not increase continuously, the value of the right endpoint minus the value of the left endpoint is less than the sum of the value of the right endpoint minus the value of the left endpoint of the continuously increasing sub interval.

Therefore, only the sum of the right end point value minus the left end point value of all continuously increasing intervals is required.

C + + code

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
class Solution {
public:
	int maxProfit(vector<int>& prices) {
		prices.push_back(-1);
		int* profit = new int[prices.size()];
		int top = 0;
		int i = 0, j = 1;
		int sum = 0;
		while (j < prices.size())
		{
			if (prices[j - 1] < prices[j])
			{
				j++;
			}
			else
			{
				if (j - 2 < 0)
				{
					i = j;
					j++;
					continue;
				}
				if (prices[j - 1] > prices[j - 2])
				{
					sum += prices[j - 1] - prices[i];
					i = j;
					j += 1;
				}
				else
				{
					i = j;
					j += 1;
				}
			}
		}
		return sum;
	}
};
int main()
{
	Solution P;
	vector<int>prices;
	int n = 0;
	while (cin >> n)
	{
		if (n == 0)break;
		prices.push_back(n);
	}
	cout<<P.maxProfit(prices);
}