101. Symmetric binary tree

Given a binary tree, check whether it is mirror symmetric.
For example, a binary tree [1,2,2,3,4,4,3] is symmetric.

    1
   / \
  2   2
 / \ / \
3  4 4  3

Method 1: recursion
Problem solving idea: recurse the left and right subtrees and judge whether they are equal.

public boolean isSymmetric(TreeNode root) {
    // Recursion and comparison of left and right subtrees of a tree.
    return recursion(root.left,root.right);
}
public boolean recursion(TreeNode leftRoot,TreeNode rightRoot){     
    if(leftRoot == null && rightRoot == null){
        return true;
    }
    if(leftRoot == null && rightRoot != null || leftRoot!= null && rightRoot == null){
        return false;
    }
    if(leftRoot.val != rightRoot.val){
        return false;
    }
    if(!recursion(leftRoot.left,rightRoot.right)){
        return false;
    }
    if(!recursion(leftRoot.right,rightRoot.left)){
        return false;
    }
    return true;
}

Method 2: hierarchy
The solution idea is to use hierarchical traversal to put the values of the left and right subtrees into the queue (mirror into), and compare whether the two adjacent values in the queue are equal. If they are not equal, they are not symmetrical binary trees.

public boolean isSymmetric(TreeNode root) {
    // queue
    Deque<TreeNode> deque = new LinkedList<>();
    deque.add(root);
    deque.add(root);
    TreeNode leftRoot,rightRoot;
    while(!deque.isEmpty()){
        leftRoot = deque.poll();
        rightRoot = deque.poll();
        if(leftRoot == null && rightRoot == null) {
            continue;
        }
        if(leftRoot == null || rightRoot == null){
            return false;
        }
        if(leftRoot.val != rightRoot.val){ 
            return false;
        }
        // Mirror insertion queue
        deque.add(leftRoot.left);
        deque.add(rightRoot.right);
        deque.add(leftRoot.right);
        deque.add(rightRoot.left);
    }
    return true;
}

102. Sequence traversal of binary tree

To give you a binary tree, please return the node values obtained by traversing in sequence. (that is, access all nodes from left to right layer by layer).
Example:
Binary tree: [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7
 Return its sequence traversal result:
[
  [3],
  [9,20],
  [15,7]
]

Problem solving idea: use the queue to store the left and right subtrees when accessing the root node. Traverse the hierarchy, put the nodes of each layer into the same array, access each layer, and add the final result set.

public List<List<Integer>> levelOrder(TreeNode root) {
    List<List<Integer>> result = new ArrayList<>();
    if(root == null){
        return result;
    }
    Deque<TreeNode> deque = new LinkedList<>();
    ArrayList<Integer> list;
    deque.add(root);
    int n;
    while(!deque.isEmpty()){
        n = deque.size();
        list = new ArrayList<>();
        for(int i = 0;i<n; i++){
            root = deque.poll();
            list.add(root.val);
            if(root.left != null){
                deque.add(root.left);
            }
            if(root.right != null){
                deque.add(root.right);
            }
        }
        result.add(list);
    }
    return result;
}

103. Zigzag sequence traversal of binary tree

Given a binary tree, return the sawtooth sequence traversal of its node value. (that is, traverse the next layer from left to right, and then from right to left, and so on, alternating between layers).
Example:
Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7
 The zigzag sequence traversal is returned as follows:
[
  [3],
  [20,9],
  [15,7]
]

Problem solving idea: use queue assistance to do hierarchical traversal. During hierarchical traversal, when storing the result set, the storage order is different according to the parity of the hierarchy. The even layer stores the elements from left to right, and the odd layer stores the elements from right to left.

public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
    List<List<Integer>> result = new ArrayList<>();
    if(root == null){
        return result;
    }
    ArrayDeque<TreeNode> deque = new ArrayDeque<>();
    LinkedList<Integer> list;
    // Even layers are false from left to right, and odd layers are true from right to left
    boolean level = false;
    deque.add(root);
    while(!deque.isEmpty()){
        int n = deque.size();
        list = new LinkedList<>();
        for(int i = 0;i < n;i++){
            root = deque.poll();
            if(level){
            	// It is stored from right to left, and the elements are stored in the first place each time. The list is a linked list, which is more efficient.
                list.add(0,root.val);
            }else{
            	// Store from left to right in sequence
                list.add(root.val);
            }
            if(root.left != null){
                deque.add(root.left);
            }
            if(root.right != null) {
                deque.add(root.right);
            }
        }
        level = !level;
        result.add(list);
    }
    return result;
}

104. Maximum depth of binary tree

Given a binary tree, find its maximum depth.
The depth of the binary tree is the number of nodes on the longest path from the root node to the farthest leaf node.
Note: leaf nodes refer to nodes without child nodes.
Example:

Given binary tree [3,9,20,null,null,15,7]，
    3
   / \
  9  20
    /  \
   15   7
 Returns its maximum depth 3.

Method 1: DFS
Problem solving idea: DFS recursion to find the maximum depth of the tree.

public int maxDepth(TreeNode root) {
    if(root == null){
        return 0;
    }
    return 1 + Math.max(maxDepth(root.left),maxDepth(root.right));
}

Method 2: BFS
Problem solving idea: BFS level traversal, the maximum level traversal is the maximum depth.

public int maxDepth(TreeNode root) {
    // BFS
    if(root == null){
        return 0;
    }
    Deque<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    int depth = 0;
    // Level traversal and record the number of layers at the same time. The number of layers is the depth.
    while(!queue.isEmpty()){
        depth++;
        int n = queue.size();
        for (int i = 0;i<n;i++){
            root = queue.poll();
            if(root.left!=null){
                queue.add(root.left);
            }
            if(root.right!=null){
                queue.add(root.right);
            }
        }
    }
    return depth;
}

105. Construct binary tree from preorder and inorder traversal sequences

Given the preorder and inorder of a tree. Construct a binary tree and return its root node.

The sequence of traversal before binary tree is:
First traverse the root node;
Then recursively traverse the left subtree;
Finally, the right subtree is traversed recursively.

The order of traversal in binary tree is:
First, recursively traverse the left subtree;
Then traverse the root node;
Finally, the right subtree is traversed recursively.

Example:

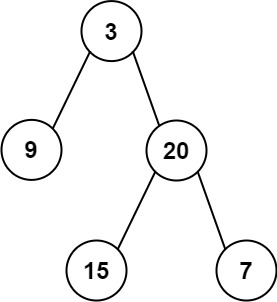
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Problem solving idea: for preorder traversal, the root node is accessed first. Only according to the root node obtained by preorder traversal, the middle order traversal is divided into left and right subtrees with the root node as the boundary. Continue to obtain the root node according to preorder traversal, and continue to divide the left and right subtrees. Repeat the above process until the left and right subtrees are empty or one node.

public TreeNode buildTree(int[] preorder, int[] inorder) {
    return recursion(preorder,inorder,0,0,inorder.length-1);
}
//pindex is the subscript pointing to the root node of the tree, inl is the left boundary of the subtree, inr is the right boundary of the subtree, and the interval range of the subtree is [inl,inr]
public TreeNode recursion(int[] preorder, int[] inorder,int pindex,int inl,int inr){     
    // When there are no elements in the interval, the subtree is empty
    if(inl > inr){
        return null;
    }
    // When there is only one element in the interval, that is, there is only one tree root node, the root node of the subtree is returned directly.
    if(inl == inr){
        return new TreeNode(preorder[pindex]);
    }
    // Create the root node of the subtree
    TreeNode root = new TreeNode(preorder[pindex]);
    // According to the root node of the subtree, the subtree is further divided into left and right subtrees. k is the subscript of the root node in inorder
    int k;
    for(k=0;k<inorder.length;k++){
        if(inorder[k] == preorder[pindex]){
            break;
        }
    }
    // The subscript of the root node of the left subtree is the subscript of the current root node plus one.
    root.left = recursion(preorder,inorder,pindex+1,inl,k-1);
    // The subscript of the root node of the right subtree is: the subscript of the current root node plus the number of elements of the left subtree + 1.
    pindex += k - inl + 1;
    root.right = recursion(preorder,inorder,pindex,k+1,inr);
    return root;
}

108. Convert an ordered array into a binary search tree

Give you an integer array nums, in which the elements have been arranged in ascending order. Please convert it into a highly balanced binary search tree.
A height balanced binary tree is a binary tree that satisfies the requirement that the absolute value of the height difference between the left and right subtrees of each node does not exceed 1.
Example:

Input: nums = [-10,-3,0,5,9]
Output:[0,-3,9,-10,null,5]

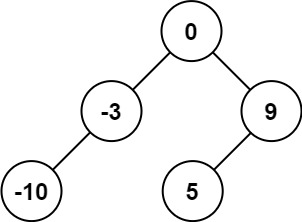
Explanation:[0,-10,5,null,-3,null,9] Will also be considered the correct answer:

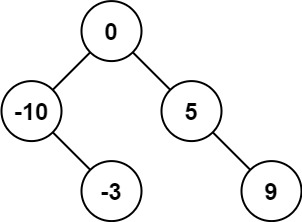
Problem solving idea: look at the whole array as a tree. The root node must be the middle value in the tree, so that the tree can be highly balanced. Only select the middle value in the tree as the root node. After selecting the middle value, divide the whole tree into left and right subtrees, continue to select the middle value as the root node of the subtree, and continue to divide the subtree until the node in the subtree is empty.

public TreeNode sortedArrayToBST(int[] nums) {
    return ArrayToBST(nums,0,nums.length-1);
}
// The left boundary of the left subtree and the right boundary of the right subtree.
public TreeNode ArrayToBST(int[] nums,int left,int right){     
    if(left > right){
        return null;
    }
    if(left == right){
        return new TreeNode(nums[left]);
    }
    int mid = left + (right-left + 1)/2;
    // Select the intermediate value as the child node.
    TreeNode root = new TreeNode(nums[mid]);
    // Partition subtree
    root.left = ArrayToBST(nums,left,mid-1);
    root.right = ArrayToBST(nums,mid+1,right);
    return root;
}

116. Populate the next right node pointer for each node

Given a perfect binary tree, all leaf nodes are in the same layer, and each parent node has two child nodes.
Definition of binary tree

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Fill in each of its next pointers so that this pointer points to its next right node. If the next right node cannot be found, set the next pointer to NULL.

Advanced:
You can only use constant level extra space.
Using recursion to solve the problem also meets the requirements. The stack space occupied by the recursive program in this problem is not considered as additional space complexity.
Example: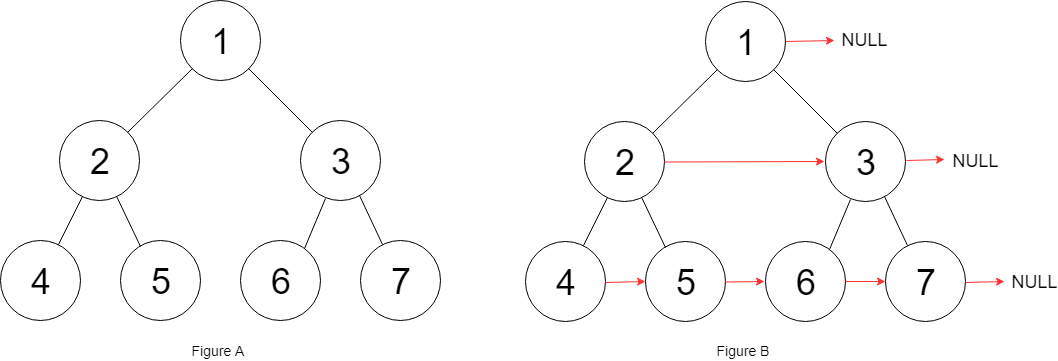

Input: root = [1,2,3,4,5,6,7]
Output:[1,#,2,3,#,4,5,6,7,#]
Explanation: the given binary tree is shown in the figure A As shown in, your function should fill each of it next Pointer to its next right node,
As shown in the figure B As shown in. The serialized output is arranged by sequence traversal, and the nodes of the same layer are composed of next Pointer connection,'#'marks the end of each layer.

Method 1: use queue hierarchy traversal and modify the next pointer

public Node connect(Node root) {
    if(root == null)
        return null;
    Deque<Node> deque = new LinkedList<>();
    Node tmp = root;
    deque.add(root);
    while(!deque.isEmpty()){
        int n = deque.size();
        for(int i = 0 ;i < n;i++) {
            root = deque.poll();
            if (i < n - 1) {
            	// Modify the next pointer to point to the next
                root.next = deque.peek();
            }
            // Full binary tree, the left is not empty, the right must not be empty
            if (root.left != null) {
                deque.add(root.left);
                deque.add(root.right);
            }
        }
    }
    return tmp;
}

Method 2: the layer is traversed from top to bottom, and the upper layer information can be used to modify this layer. When traversing each layer, make the left node point to the right node and the right node point to the left node of the next node of the parent node (root.left.next = root.right, root.right.next = root.next.left)
Recursive version

public Node connect(Node root) {
    if(root == null){
        return null;
    }
    // If there are child nodes
    if(root.left!=null){
    	// The left node points to the right node
        root.left.next = root.right;
        // If there is a next node
        if(root.next != null){
        	// The right node points to the left node of the next node
            root.right.next = root.next.left;
        }
    }
    connect(root.left);
    connect(root.right);
    return root;
}

Non recursive version

public Node connect(Node root) {
    if(root == null){
        return null;
    }
    Node tmp = root,left;
    // If the left node is not empty, it indicates that there is a next layer
    while(root.left!=null){
    	// Save left node
        left = root.left;
        root.left.next = root.right;
        // Traverse the whole layer
        while(root.next != null){
            root.right.next = root.next.left;
            root = root.next;
            root.left.next = root.right;
        }
        // Go to the next floor
        root = left;
    }
    return tmp;
}

118. Yanghui triangle

Given a nonnegative integer numRows, the first numRows of the Yang Hui triangle are generated.
In the Yang Hui triangle, each number is the sum of its upper left and upper right numbers.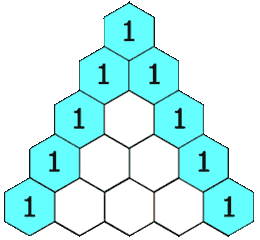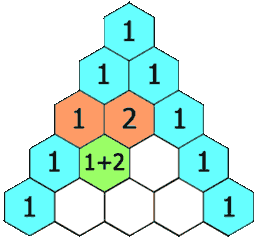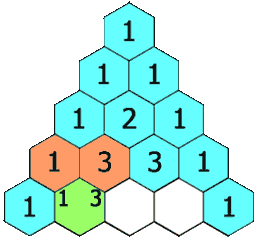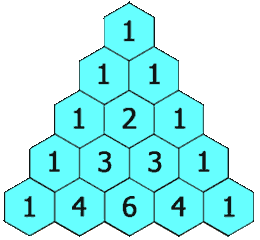
Example:

input: numRows = 5
 output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

Solution idea: according to the definition of Yang Hui triangle.

public List<List<Integer>> generate(int numRows) {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> list;
    for(int i = 0; i < numRows;i++){
        list = new ArrayList<>();
        for (int j = 0; j <= i; ++j) {
            // The first and last element is 0
            if (j == 0 || j == i) {
                list.add(1);
            } else {
                // The middle element is the sum of the element values in the previous line
                list.add(result.get(i - 1).get(j - 1) + result.get(i - 1).get(j));
            }
        }
        result.add(list);
    }
    return result;
}

121. The best time to buy and sell stocks

Given an array of prices, its ith element prices[i] represents the price of a given stock on day I.
You can only choose to buy this stock one day and sell it on a different day in the future. Design an algorithm to calculate the maximum profit you can make.
Return the maximum profit you can make from this transaction. If you can't make any profit, return 0.

Input:[7,1,5,3,6,4]
Output: 5
 Explanation: on day 2 (stock price) = 1)When buying, on day 5 (stock price) = 6)When you sell,
Maximum profit = 6 - 1 = 5 . 
Note that the profit cannot be 7 - 1 = 6, Because the selling price needs to be greater than the buying price; At the same time, you can't sell stocks before buying.

Problem solving idea: adopt dynamic programming and consider finding the maximum profit on day n. The price on day n minus the previous lowest price and the maximum profit on day n-1 shall be taken as the maximum value. Only the lowest price before day n and the maximum profit on day n-1 need to be stored.

public int maxProfit(int[] prices) {
	// The maximum profit on day 0 is 0
    int maxProfit = 0;
    // The minimum price is initialized to the maximum value
    int minPrice = Integer.MAX_VALUE;
    for(int i = 0;i < prices.length;i++){
    	// Iteration for maximum profit. It is the maximum value of the current maximum profit and the current price and the previous minimum price.
        maxProfit = Math.max(maxProfit,prices[i] - minPrice);
        if(minPrice > prices[i]){
            minPrice = prices[i];
        }
    }
    return maxProfit;
}

122. The best time to buy and sell stocks II

Give an array prices, where prices[i] is the price of a given stock on day I.
Design an algorithm to calculate the maximum profit you can make. You can complete as many transactions as possible (buying and selling a stock multiple times).
Note: you cannot participate in multiple transactions at the same time (you must sell the previous shares before buying again).
Example:

input: prices = [7,1,5,3,6,4]
output: 7
 explain: On day 2 (stock price) = 1)When buying, on day 3 (stock price) = 5)Sell at, 
The exchange is profitable = 5-1 = 4 . 
Then, on day 4 (stock price) = 3)When buying, on day 5 (stock price) = 6)Sell at, 
The exchange is profitable = 6-3 = 3 . 

Method 1: go back and consider all the possibilities.
Backtracking pruning algorithm: timeout

public int maxProfit(int[] prices) {
    // Backtracking pruning
    return maxProfit(prices,0,0,true,0);
}
public int maxProfit(int[] prices,int n,int maxProfig,boolean flag,int p) {
    if(n == prices.length){
        return maxProfig;
    }
    if(flag){
        // No stock
        // Select buy or not to return to the maximum value
        return Math.max(maxProfit(prices,n+1,maxProfig,false,n),
                maxProfit(prices,n+1,maxProfig,true,n));
    }else{
        // Existing stock
        // Choose to sell
        return Math.max(maxProfit(prices,n + 1,maxProfig,false,p),
                prices[n]>prices[p]?maxProfit(prices,n+1,maxProfig + prices[n]
                -prices[p],true,p):Integer.MIN_VALUE);
    }
}

Method 2: greed
Solution: as long as the price of the next day is higher than that of the previous day, the maximum profit will be calculated.
As shown in the figure: just add up the values of all rising curves.

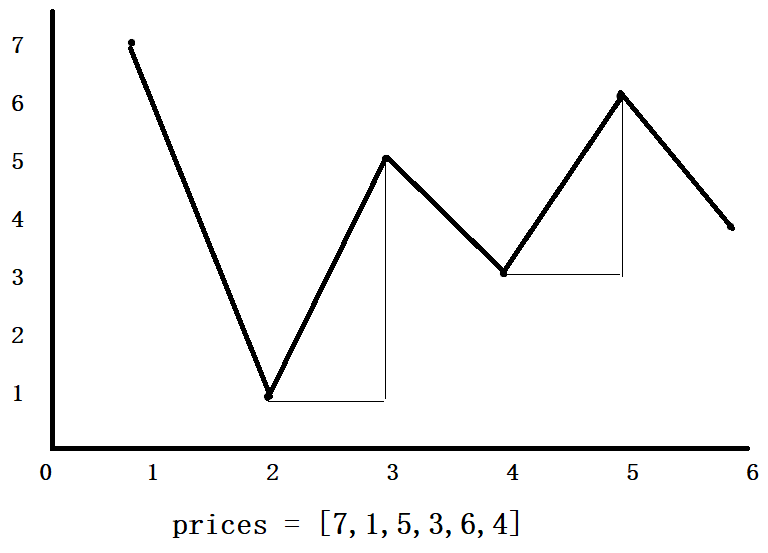
public int maxProfit(int[] prices) {
    int profit = 0;
    for(int i = 1;i < prices.length;i++){
        profit += Math.max(prices[i] - prices[i-1],0);
    }
    return profit;
}

Method 3: dynamic programming
Considering that "you can't participate in multiple transactions at the same time", you can only have one stock or no stock after the end of each transaction.
Definition status dp[i][0] indicates the maximum profit of holding no stock after trading on day I, and dp[i][1] indicates the maximum profit of holding a stock after trading on day I (I starts from 0).
State transition equation:
dp[i][0] may not have stocks the day before, or there may be stocks, but they are sold and gain the income of prices[i]. The state transition equation is:
dp[i][0] = max{ dp[i−1][0], dp[i−1][1] + prices[i] }
dp[i][1] you may or may not have stocks the day before, but you bought stocks today and spent cash. The state transition equation is:
dp[i][1] = max{ dp[i−1][1],dp[i−1][0]−prices[i] }
Consider the initial state:
dp[0][0] = 0. After the end of the transaction on day 0, the income from holding cash is 0
dp[0][1] = -prices[0] after the end of trading on day 0, the income from holding shares is - prices[0], and money is exchanged for shares.
Finally, dp[n-1][0] returned must be greater than or equal to dp[n-1][1]

Optimization: since the state transition equation is only related to the state of the previous day, only two variables need to be used. dp0 represents the maximum profit from holding cash the previous day. dp1 represents the maximum profit from holding shares the previous day.

public int maxProfit(int[] prices) {
	// Initialization status
    int dp0 = 0,dp1 = -prices[0];
    for(int i=1; i < prices.length; i++){
    	// Update status
        dp0 = Math.max(dp0,dp1 + prices[i]);
        dp1 = Math.max(dp1,dp0 - prices[i]);
    }
    return dp0;
}