49. Alphabetic word grouping

You are given an array of strings. Please group the heterographic words together. A list of results can be returned in any order.
Alphabetic words are new words that result from rearranging the letters of the source word, and the letters in all source words are usually used exactly once.
Example:

input: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
output: [["bat"],["nat","tan"],["ate","eat","tea"]]

Solution ideas: Ectopic words have the same letters but different locations, so you can use a count of the number of times the letters appear in the word. Each letter in the ectopic word must appear the same number of times.

public List<List<String>> groupAnagrams(String[] strs) {
    Map<String, List<String>> map = new HashMap<>();
    int[] counts = new int[26];
    for(int i = 0; i<strs.length; i++){
        for(int j = 0;j<strs[i].length();j++){
            counts[strs[i].charAt(j)-'a']++;
        }
        StringBuffer sb = new StringBuffer();
        for(int k = 0;k<26;k++){
            if(counts[k]!=0){
                sb.append(k+'a');
                sb.append(counts[k]);
                counts[k] = 0;
            }
        }
        String s = sb.toString();
        if(map.containsKey(s)){
            map.get(s).add(strs[i]);
        }else{
            ArrayList<String> list = new ArrayList<>();
            list.add(strs[i]);
            map.put(s,list);
        }
    }
    return new ArrayList<>(map.values());
}

50. Pow(x, n)

Implement pow(x, n), which is the n-th power function of X (that is, x n).
Example:

Input: x = 2.00000, n = 10
 Output: 1024.00000

Input: x = 2.10000, n = 3
 Output: 9.26100

Input: x = 2.00000, n = -2
 Output: 0.25000
 Interpretation: 2-2 = 1/22 = 1/4 = 0.25

Solving ideas: Only two cases of N need to be considered, when n is less than 0, the result is 1/result, when n is greater than 0, the result is result, when n is equal to 0, the result is 1, using fast power algorithm, x_x2_x 4_x 8..., on the basis of the previous result, continue to power to achieve the power required for fast approximation.

public double myPow(double x, int n) {
    double result = 1, t = x;
    long pn = 1,i = n;
    if(n < 0){
        i = -i;
    }
    while(i > 0){
        if (pn*2 < i) {
        	// Continue exponentiation each time based on the previous result
            t *= t;
            pn = pn * 2;
        } else {
        	// Add the temporary result to the final result, i-pn, and continue to calculate the remaining power
            result *= t;
            i -= pn;
            // Initialization Conditions
            t = x;
            pn = 1; 
        }
    }
    if(n<0){
        result = 1/result;
    }
    return result;
}

53. Maximum Subarray and

Give you an integer array nums, find a continuous subarray with the largest sum (the subarray contains at least one element) and return its maximum sum. The subarray is a continuous part of the array.
Example:

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
 Interpretation: Continuous subarrays [4,-1,2,1] And max, 6.

Solution ideas: Greedy algorithm, if the front and greater than 0, keep, otherwise, from the next start to find the maximum value.

public int maxSubArray(int[] nums) {
    int max = Integer.MIN_VALUE;
    int t = 0;
    for(int i = 0;i<nums.length;i++){
        if(t + nums[i] > 0){
            t += nums[i];
            max = Math.max(t,max);
        }else{
            t = 0;
            max = Math.max(nums[i],max);
        }
    }
    return max;
}

54. Spiral Matrix

Give you a matrix of m rows and n columns. Return all elements of the matrix in a clockwise spiral order.
Example:

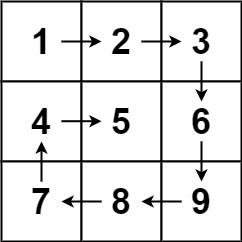
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output:[1,2,3,6,9,8,7,4,5]

Solve the problem by finding the four upper and lower boundary values. Loop through four, and record the number of elements that have been visited. When all elements have been visited, jump out.

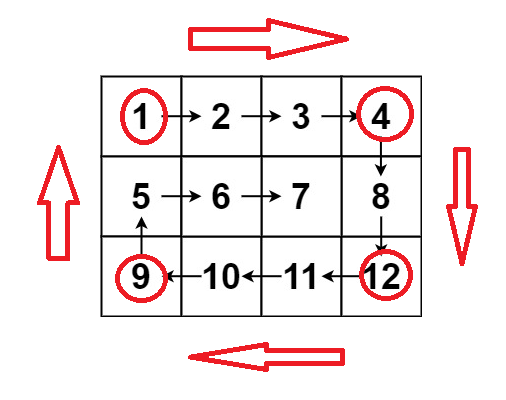
Each layer is divided into four loops.

public List<Integer> spiralOrder(int[][] matrix) {
    List<Integer> result = new ArrayList<>();
    int m = matrix.length;
    int n = matrix[0].length;
    int num = m*n;
    int left,right,top,bottom;       // Record the top, bottom, left and right boundary values, respectively.
    left = 0;
    right = n-1;
    top = 0;
    bottom = m-1;
    while(num > 0){
    	// Each layer is divided into four loops, with elements added clockwise to the result set.
        for(int i = left; i <= right && num > 0; i++){ 
            result.add(matrix[top][i]);
            num--;
        }
        for(int i = top + 1; i <= bottom && num > 0;i++){
            result.add(matrix[i][right]);
            num--;
        }
        for(int i = right - 1;i >= left && num > 0;i--){
            result.add(matrix[bottom][i]);
            num--;
        }
        for(int i = bottom - 1;i > top && num > 0;i--){
            result.add(matrix[i][left]);
            num--;
        }
        left++;
        top++;
        right--;
        bottom--;
    }
    return result;
}

55. Jump Game

Given a non-negative integer array nums, you are initially positioned at the first subscript of the array. Each element in the array represents the maximum length you can jump at that location. Determine if you can reach the last subscript.
Solution ideas: If the current value that can be skipped is greater than or equal to the length of the array, then the last subscript can be reached. If the value currently available to jump is 0, then you can't jump. Traverse through the array, each time looking for the maximum value that can be skipped, go one step forward and subtract the value that can be skipped by one.

public boolean canJump(int[] nums) {
    int max = Integer.MIN_VALUE;
    // foreach
    for(int i = 0; i < nums.length - 1; i++){
    	// For each element accessed, compare values and select the maximum value that can be skipped.
        max = Math.max(max,nums[i]);
        // If the value that can be skipped is less than or equal to 0, the end point will not be skipped.
        if(max <= 0){
            return false;
        }
        // If the value that can be skipped is greater than or equal to the value of the last subscript of the array, the end point can be skipped.
        if(max >= nums.length - 1){
            return true;
        }
        max--;
    }
    //If you jump out of the loop above, you have reached the last subscript element and return true.
    return true;
}

56. Consolidation interval

Represents a set of intervals in the array intervals, where a single interval is intervals[i] = [starti, endi]. Please merge all the overlapping intervals and return a non-overlapping interval array that exactly covers all the intervals in the input.

Example 1:
Input: intervals = [[1,3],[2,6],[8,10],[15,18]]
Output:[[1,6],[8,10],[15,18]]
Interpretation: Interval [1,3] and [2,6] overlap, Merge them into [1,6].

Example 2:
Input: intervals = [[1,4],[4,5]]
Output:[[1,5]]
Interpretation: Interval [1,4] and [4,5] They can be considered overlapping intervals.

Solving ideas: Sort the arrays in ascending order by the left endpoint. The array is then traversed and merged if the intervals are found to be coincident. When the left end point of the latter interval is less than or equal to the right end point of the previous interval, the two intervals are coincident and merged. The right end point after merging takes the maximum value of the two intervals.

public int[][] merge(int[][] intervals) {
    // Sort Arrays
    Arrays.sort(intervals, new Comparator<int[]>() {
        @Override
        public int compare(int[] o1, int[] o2) {
            return o1[0] - o2[0];
        }
    });
    int start = intervals[0][0],end = intervals[0][1];
    List<int[]> merged = new ArrayList<>();
    for(int i = 1; i < intervals.length; i++){
    	// The right end of the previous interval is at the right end of this interval, and the intervals are coincident for merging
        if(intervals[i][0] <= end){
            end = Math.max(end,intervals[i][1]);
        }else{
        	// No coincidence, add the final result.
            merged.add(new int[]{start,end});
            start = intervals[i][0];
            end = intervals[i][1];
        }
    }
    merged.add(new int[]{start,end});
    return merged.toArray(new int[merged.size()][]);
}

62. Different paths

A robot is located in the upper left corner of an m x n grid (the starting point is marked as "Start" in the image below).
The robot can only move down or right one step at a time. The robot tries to reach the lower right corner of the grid (marked Finish in the image below). How many different paths are there in total?
Example:

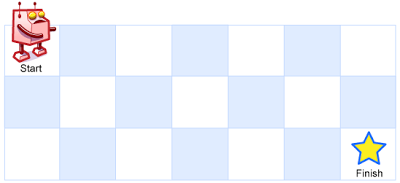
Input: m = 3, n = 7
 Output: 28

Solving ideas: Dynamic planning, using dp[i][j] to indicate how many paths there are to i,j's location. To reach i,j, you can only start at i-1, j, or i,j-1. So the value of dp[i][j] is dp[i-1][j] + dp[i][j-1]. For an m*n grid, dp[m-1][n-1] is the final answer because the array subscript starts at 0. The initial condition for dynamic programming is that there is only one path to the i,0 position, because the robot can only go down or right, as is the case for 0 and J.

public int uniquePaths(int m, int n) {     
    int[][] dp = new int[m][n];
    // Initialize Initial Value
    for(int i = 0;i < n; i++){
        dp[0][i] = 1;
    }
    for(int i = 0;i < m; i++){
        dp[i][0] = 1;
    }
    // Fill in the form
    for(int i = 1;i<m;i++){
        for(int j=1;j<n;j++){
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

66.Add one

Given a non-negative integer represented by a non-empty array of integers, add one to it.
The highest number of digits is placed at the top of the array, where each element only stores a single number.
You can assume that this integer does not start with zero except for the integer 0.
Solution ideas: Consider the array overflow problem, if the array is all 9, plus 1 after completion, you also need to expand the array by one bit to complete the carry.

public int[] plusOne(int[] digits) {
    for(int i = digits.length-1;i>= 0; i--){
        digits[i] += 1;
        if(digits[i] < 10){
            return digits;
        }else{
            digits[i] = 0;
        }
    }
    // All 9
    int[] result = new int[digits.length+1];
    result[0] = 1;
    return result;
}

69. Sqrt(x)

Give you a non-negative integer x, calculate and return the arithmetic square root of X.
Since the return type is an integer, only the integer part of the result is retained, and the decimal part is discarded.
Note: No built-in exponential functions and operators, such as pow(x, 0.5) or x ** 0.5, are allowed.
Solution ideas: Binary search, clip out the final value.

public int mySqrt(int x) {
    double L = 0;
    double R = x;
    double mid;
    while(L < R){
        mid = L + (R - L)/2;
        if((long)mid * (long)mid <= x && x <= (long)(mid + 1)*(long)(mid+1)){
            if((long)(mid+1) *(long)(mid+1) == x){
                return (int)(mid+1);
            }
            return (int)mid;
        }else if(mid*mid < x){
            L = mid;
        }else{
            R = mid;
        }
    }
    return 0;
}

70. Climb the stairs

Suppose you are climbing the stairs. You need n steps to reach the roof.
You can climb one or two steps at a time. How many different ways do you have to climb to the top?
Note: given n is a positive integer.
Solving ideas: Dynamic planning, dp[i] is the number of methods to reach step I I. To climb to step I i, you can either climb one step from step I-1 or two steps from step i-2. In this way, the number of methods to reach step I I-1 and I-2 will be converted. The transfer equation for dynamic programming is dp[i] = dp[i-1] + dp[i-2]. Initial condition i = 1, dp[1] = 1, i = 2, dp[2] = 2.
The first step in the program is only related to i-1, i-2, and the other states before it need not be stored.

public int climbStairs(int n) {
    if(n <= 2){
        return n;
    }
    int[] dp = new int[3];
    dp[0] = 1;
    dp[1] = 2;
    for(int i = 2;i < n; i++){
        dp[2] = dp[0]+dp[1];
        dp[0] = dp[1];
        dp[1] = dp[2];
    }
    return dp[2];
}