Title Source: https://leetcode-cn.com/problems/max-area-of-island/
Original solution: https://leetcode-cn.com/problems/max-area-of-island/solution/biao-zhun-javadong-tai-gui-hua-jie-fa-100-by-mark-/
Maximum area of the island
- Give you a binary matrix grid of size m x n.
- An island is a combination of some adjacent 1s (representing land). The "adjacent" here requires that two 1s must be adjacent in four horizontal or vertical directions. You can assume that the four edges of the grid are surrounded by 0 (representing water).
- The area of an island is the number of cells on the island with a value of 1.
Calculate and return the largest island area in the grid. If there are no islands, the return area is 0.
Example
For a grid, it is a choice for a grid to be [[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,, 1,1,0,0,0], [0,0,0,0,0,0,1,0,0,0,0,0]
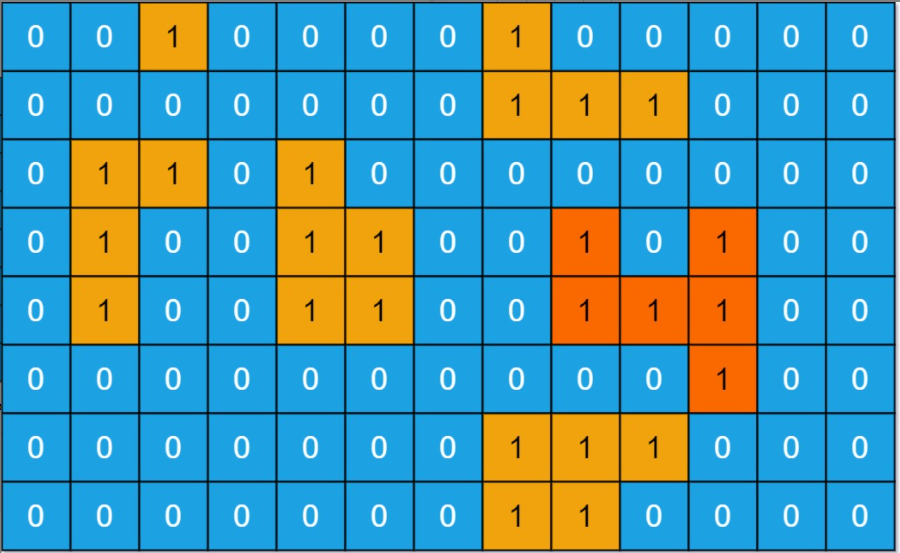
Output: 6
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0
Tips
① m == grid.length
② n == grid[i].length
③ 1 <= m, n <= 50
④ grid[i][j] is 0 or 1
According to the meaning of the topic, you can immediately interpret the meaning of the topic: obtain the area of each island and return with the maximum area. The easiest idea to think of is to use depth first search DFS to forcibly traverse all blocks of each island.
To obtain the area of each island, it is natural to traverse all blocks of the whole map. When encountering land, it will search the nearby land from the coordinates of the land and count the land area. However, if we traverse the whole map, we will naturally encounter such a situation: we visit the land area block a1, and then obtain all blocks (a1,a2,a3,a4) of the whole island a according to the time resources consumed by a1, and then continue to traverse the map and access a2, and again consume time resources to obtain the blocks of island a we have obtained.
In this case, it is not difficult for us to think of creating a hash table to store all accessed blocks. In this way, when we visit the island, we will add all blocks of the whole island to the island hash table. When accessing the land in the future, we only need to judge whether the block contains in the hash table first, so as to avoid consuming resources to obtain the block information we have obtained.
However, this problem only needs to find the maximum area of the island, and a large amount of data stored in the hash table will undoubtedly occupy unnecessary memory resources. We will consider clearing the relevant contents of the hash table after obtaining the area of the island, but this will affect our original intention of creating the hash table (if the currently accessed block has been explored, it will not be accessed). So we can process the explored islands directly on the map.
Treatment method: when encountering land, search all connected land starting from land, count the total area of the island, and turn the island into an ocean. In this way, once the island information is recorded, it will disappear from the map, and the subsequent map traversal will not scan any explored islands, which greatly reduces the consumption of memory resources.
Examples of ideas:
The first is to customize a map, which has only one island. The purpose is to show how to obtain the whole island according to one land.

① start traversing from the starting point of the map and try to encounter the first land block
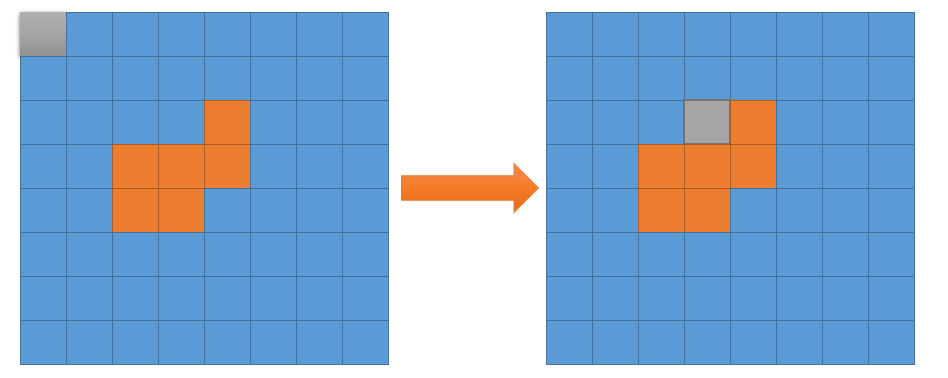
② visit the land block, set the island area as 1, try to visit the surrounding blocks, and turn yourself into an ocean at the same time
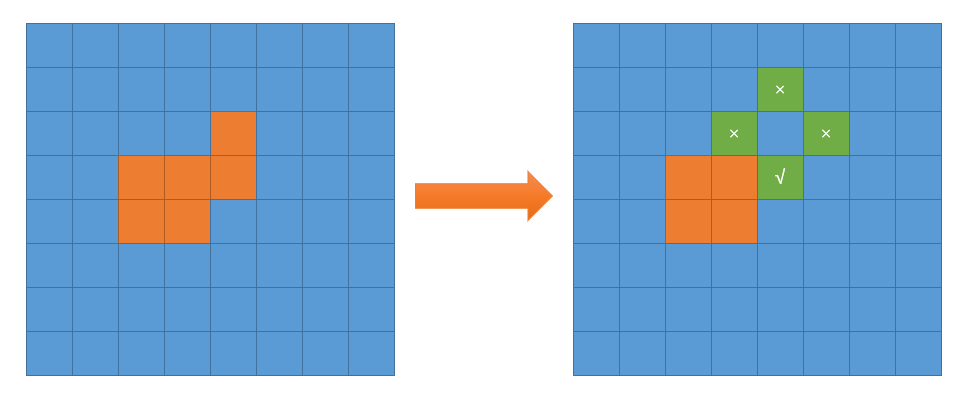
③ analogy
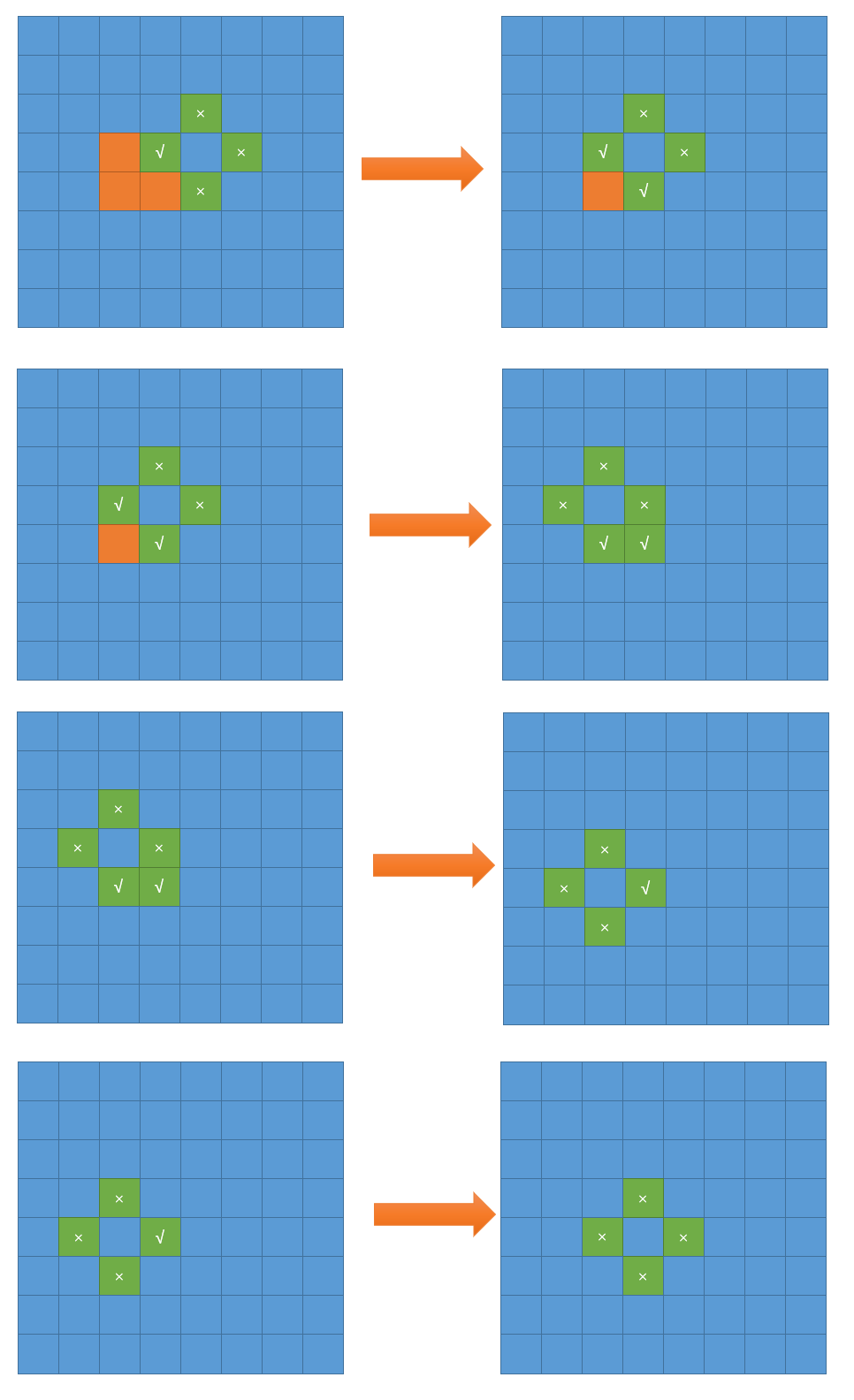
As can be seen from the figure, for each land block, recursively explore its four direction blocks. If the land continues to recursively explore, the area of the whole island can be obtained finally.
This problem can be solved by defining a max to store the maximum area.
public int maxAreaOfIsland(int[][] grid) {
int maxArea = 0;
int height = grid.length;
int width = grid[0].length;
//Determine whether each block is land
//If it's land, turn the land into an ocean after recording
for (int i = 0; i < height; i++) {
for (int j = 0; j < width; j++) {
if (grid[i][j] == 1) {
int area = dfs(i, j, grid);
if (area > maxArea)
//Replace if the new island is larger
maxArea = area;
}
}
}
return maxArea;
}
public int dfs(int i, int j, int[][] grid) {
int height = grid.length;
int width = grid[0].length;
//Conditions for executing this function
// 1. The coordinates of the block are reasonable
// 2. The block content is land
//★ although it is explicitly mentioned in the maxArea function that only land can access the function, this function will search around by itself. It is necessary to avoid executing the function in the searched marine block ★
if (i < 0 || j < 0 ||
i >= height || j >= width ||
grid[i][j] == 0) {
return 0;
}
//This step indicates that the block is land
//Block area
int area = 1;
//Turn the block into an ocean
grid[i][j]=0;
//Search down
area += dfs(i + 1, j, grid);
//Search up
area += dfs(i - 1, j, grid);
//Search right
area += dfs(i, j + 1, grid);
//Search left
area += dfs(i, j - 1, grid);
return area;
}
public class max_area_of_island {
public int maxAreaOfIsland(int[][] grid) {
int maxArea = 0;
for (int i = 0; i < grid.length; i++)
for (int j = 0; j < grid[0].length; j++)
if (grid[i][j] == 1)
maxArea = Math.max(maxArea, dfs(i, j, grid));
return maxArea;
}
public int dfs(int i, int j, int[][] grid) {
if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == 0)
return 0;
int area = 1;
grid[i][j] = 0;
area += dfs(i + 1, j, grid);
area += dfs(i - 1, j, grid);
area += dfs(i, j + 1, grid);
area += dfs(i, j - 1, grid);
return area;
}
public static void main(String[] args) {
max_area_of_island demo = new max_area_of_island();
System.out.println(demo.maxAreaOfIsland(new int[][]{
{0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0},
{0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0},
{0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0}}
));
}
}
public class max_area_of_island {
public int maxAreaOfIsland(int[][] grid) {
int maxArea = 0;
for (int i = 0; i < grid.length; i++)
for (int j = 0; j < grid[0].length; j++)
if (grid[i][j] == 1)
maxArea = Math.max(maxArea, dfs(i, j, grid));
return maxArea;
}
public int dfs(int i, int j, int[][] grid) {
if (i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == 0)
return 0;
int area = 1;
grid[i][j] = 0;
area += dfs(i + 1, j, grid);
area += dfs(i - 1, j, grid);
area += dfs(i, j + 1, grid);
area += dfs(i, j - 1, grid);
return area;
}
public static void main(String[] args) {
max_area_of_island demo = new max_area_of_island();
System.out.println(demo.maxAreaOfIsland(new int[][]{
{0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0},
{0, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0},
{0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0}}
));
}
}
Execution time: 2 ms, beating 99.73% of users in all Java submissions
Memory consumption: 38.9 MB, beating 60.41% of users in all Java submissions