leetcode lecture on algorithm interview in Dachang 18. Queue
Video Explanation (efficient learning): Click to learn
catalog:
6. Depth first & breadth first
10. Recursion & divide and conquer
- Queue features: first in first out (FIFO)
- Time complexity of queue: queue in and queue out O(1), find O(n)
- Priority queue: priorityQueue, queue out according to priority, and realize Heap(Binary,Fibonacci...)
- js does not have a queue, but it can be simulated with an array

225. Implement stack with queue (easy)
Method 1. Use two queues to implement
- Idea: it's no practical significance to investigate the familiarity of the stack and queue. Two queues can be used to realize the function of the stack, but the order of importing data from one queue into the other queue remains unchanged, so one queue is only used for backup. In the code, queue2 is the backup queue. When entering the stack, queue 1 enters the queue, When leaving the stack, if queue 1 is empty, queue 1 and queue 2 are exchanged to add all the elements of the backup queue to queue 1, and then all but the last element in queue 1 are dequeued and added to the backup queue,
- Complexity analysis: the time complexity of push is O(1) and that of pop is O(n). Spatial complexity O(n), where n is the number of elements in the stack, which is stored in two queues
The animation is too large. Click to view it
Js:
var MyStack = function() {
this.queue1 = [];
this.queue2 = [];//Backup queue
};
MyStack.prototype.push = function(x) {
this.queue1.push(x);
};
MyStack.prototype.pop = function() {
// Reduce the number of exchanges between two queues. Only when queue1 is empty, two queues are exchanged
if(!this.queue1.length) {
[this.queue1, this.queue2] = [this.queue2, this.queue1];
}
while(this.queue1.length > 1) {//When the number of elements in queue 1 is greater than 1, the elements are continuously push ed into the backup queue
this.queue2.push(this.queue1.shift());
}
return this.queue1.shift();//Finally, the last element of queue 1 is dequeued
};
MyStack.prototype.top = function() {
const x = this.pop();//Check the top of the stack, queue out, and then push in queue 1
this.queue1.push(x);
return x;
};
MyStack.prototype.empty = function() {
return !this.queue1.length && !this.queue2.length;
};
Java:
class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
public MyStack() {
queue1 = new LinkedList<>();
queue2 = new LinkedList<>();
}
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()){
queue2.offer(queue1.poll());
}
Queue<Integer> queueTemp;
queueTemp = queue1;
queue1 = queue2;
queue2 = queueTemp;
}
public int pop() {
return queue1.poll();
}
public int top() {
return queue1.peek();
}
public boolean empty() {
return queue1.isEmpty();
}
}
Method 2. Use a queue implementation
The animation is too large. Click to view it
- Idea: use a queue implementation. When entering the stack, just push it directly into the queue. When leaving the stack, all elements except the last element are added to the end of the queue.
- Complexity analysis: the time complexity of push is O(1), the time complexity of pop is O(n), and the space complexity is O(n)
js:
var MyStack = function() {
this.queue = [];
};
MyStack.prototype.push = function(x) {
this.queue.push(x);
};
MyStack.prototype.pop = function() {
let size = this.queue.length;
while(size-- > 1) {//Add all elements except the last element to the end of the queue.
this.queue.push(this.queue.shift());
}
return this.queue.shift();
};
MyStack.prototype.top = function() {
const x = this.pop();//First out of the stack, then in the queue
this.queue.push(x);
return x;
};
MyStack.prototype.empty = function() {
return !this.queue.length;
};
java:
class MyStack {
Deque<Integer> queue1;
public MyStack() {
queue1 = new ArrayDeque<>();
}
public void push(int x) {
queue1.addLast(x);
}
public int pop() {
int size = queue1.size();
size--;
while (size-- > 0) {
queue1.addLast(queue1.peekFirst());
queue1.pollFirst();
}
int res = queue1.pollFirst();
return res;
}
public int top() {
return queue1.peekLast();
}
public boolean empty() {
return queue1.isEmpty();
}
}
703. The K-th largest element in the data stream (easy)
Method 1: violence ranking
- Idea: when there are new elements in the data stream, re sort the array in ascending order. The last k element is the largest k element
- Complexity analysis: time complexity O(c*zlogz), z is the longest length of the data stream, C is the number of added elements, and the sorting complexity is O(zlogz). If you add C sorting, you need to sort c times.
Method 2: heap
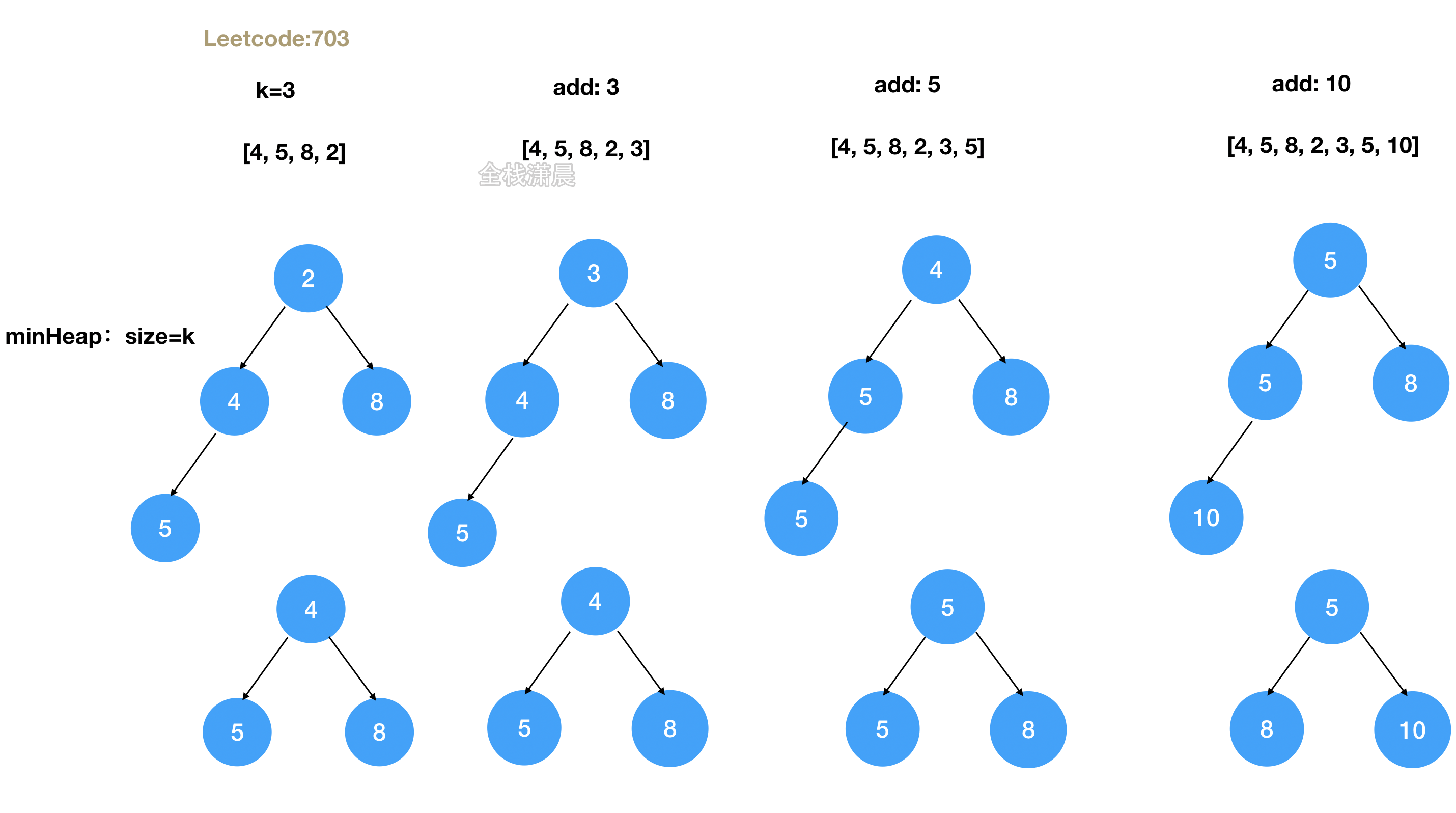
- The idea is to store the first k elements with a size, which is K's small top stack. The top is the smallest element. In the process of cyclic array, elements are added continuously and the positions of elements in the heap are adjusted. If the priority queue size is larger than k, we need to pop-up the queue header elements to ensure that the priority queue size is K. Finally, the top of the heap is the position of the k-th element
- Complexity analysis: time complexity O(nlogk), n is the size of the initial array, K is the size of the heap, the complexity of the initial heap and single insertion into the heap are O(logk), and each number of the array must be inserted into the heap once, so it is O(nlogk). Space complexity: O(k), that is, the size of the heap
js:
var KthLargest = function (k, nums) {
this.k = k;
this.heap = new Heap();
for (const x of nums) {//Add the number in the array to the small top heap
this.add(x);//Add small top pile
}
};
KthLargest.prototype.add = function (val) {
this.heap.offer(val);//Add heap
if (this.heap.size() > this.k) {//If the size exceeds the size of the small top heap, delete the smallest element from the small top heap
this.heap.poll();//Delete the smallest element
}
return this.heap.peek();//Return to the top of the heap
};
class Heap {
constructor(comparator = (a, b) => a - b, data = []) {
this.data = data;
this.comparator = comparator;//comparator
this.heapify();//Heap
}
heapify() {
if (this.size() < 2) return;
for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
this.bubbleDown(i);//bubbleDown operation
}
}
peek() {
if (this.size() === 0) return null;
return this.data[0];//View the top of the heap
}
offer(value) {
this.data.push(value);//Add array
this.bubbleUp(this.size() - 1);//Adjust the position of the added elements in the small top heap
}
poll() {
if (this.size() === 0) {
return null;
}
const result = this.data[0];
const last = this.data.pop();
if (this.size() !== 0) {
this.data[0] = last;//Swap the first and last elements
this.bubbleDown(0);//bubbleDown operation
}
return result;
}
bubbleUp(index) {
while (index > 0) {
const parentIndex = (index - 1) >> 1;//Location of parent node
//If the current element is smaller than the element of the parent node, the positions of the current node and the parent node are exchanged
if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
this.swap(index, parentIndex);//Swap the location of yourself and the parent node
index = parentIndex;//Continuously take up the parent node for comparison
} else {
break;//If the current element is larger than the element of the parent node, it does not need to be processed
}
}
}
bubbleDown(index) {
const lastIndex = this.size() - 1;//Location of the last node
while (true) {
const leftIndex = index * 2 + 1;//Location of left node
const rightIndex = index * 2 + 2;//Location of the right node
let findIndex = index;//Location of the bubbleDown node
//Find the node with small value in the left and right nodes
if (
leftIndex <= lastIndex &&
this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
) {
findIndex = leftIndex;
}
if (
rightIndex <= lastIndex &&
this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
) {
findIndex = rightIndex;
}
if (index !== findIndex) {
this.swap(index, findIndex);//Swap the current element and the small value in the left and right nodes
index = findIndex;
} else {
break;
}
}
}
swap(index1, index2) {//Swap the positions of the two elements in the heap
[this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
}
size() {
return this.data.length;
}
}
java:
class KthLargest {
PriorityQueue<Integer> pq;
int k;
public KthLargest(int k, int[] nums) {
this.k = k;
pq = new PriorityQueue<Integer>();
for (int x : nums) {
add(x);
}
}
public int add(int val) {
pq.offer(val);
if (pq.size() > k) {
pq.poll();
}
return pq.peek();
}
}
23. Merge K ascending linked lists (hard)
Methods 1. Divide and treat

- Idea: merge from bottom to top. Merge 2 linked lists for the first time and 4 linked lists for the second time... Merge two ordered linked lists each time until all the divided and ruled linked lists are merged
- Complexity: time complexity O(n * logk). N is the number of nodes in each linked list and the number of k linked lists. For each merging, the number of linked lists is less than half, and the complexity is O(logk). Merging two linked lists into one order. The complexity of the linked list is O(2n), so the time complexity is O(n * logk). The space complexity is O(logk), that is, the recursive space complexity
js:
//Merge from top to bottom, divide first and combine
var mergeKLists = function (lists) {
// When it is an empty array
if (!lists.length) {
return null;
}
// Merge two sort linked lists
const merge = (head1, head2) => {
let dummy = new ListNode(0);
let cur = dummy;
// New linked list, the new value is small, who will take it first
while (head1 && head2) {
if (head1.val < head2.val) {
cur.next = head1;
head1 = head1.next;
} else {
cur.next = head2;
head2 = head2.next;
}
cur = cur.next;
}
// If there is anything left behind, connect the rest
cur.next = head1 == null ? head2 : head1;
return dummy.next;
};
const mergeLists = (lists, start, end) => {
if (start + 1 == end) {
return lists[start];
}
// The K sorting linked lists entered can be divided into two parts, the first k/2 linked list and the last k/2 linked list
// If the first k/2 linked lists and the last k/2 linked lists are merged into two sorted linked lists, and then the two sorted linked lists are merged, all linked lists are merged
let mid = (start + end) >> 1;
let head1 = mergeLists(lists, start, mid);
let head2 = mergeLists(lists, mid, end);
return merge(head1, head2);
};
return mergeLists(lists, 0, lists.length);
};
//Bottom up consolidation
var mergeKLists = function (lists) {
if (lists.length <= 1) return lists[0] || null;//When there is only one merged node, this node is returned
const newLists = [];
//Merge from bottom to top, merge the linked list with size 2 for the first time, and merge the linked list with size 4 for the second time
for (let i = 0; i < lists.length; i += 2) {
newLists.push(merge(lists[i], lists[i + 1] || null));
}
return mergeKLists(newLists);
};
const merge = (list_1, list_2) => {//Merge two ordered linked lists
const dummyNode = new ListNode(0);
let p = dummyNode;
while (list_1 && list_2) {
if (list_1.val < list_2.val) {//Add small nodes first
p.next = list_1;
list_1 = list_1.next;
} else {
p.next = list_2;
list_2 = list_2.next;
}
p = p.next;
}
p.next = list_1 ? list_1 : list_2;//Nodes remaining after traversal
return dummyNode.next;
};
java:
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return mergeLists(lists, 0, lists.length - 1);
}
public ListNode mergeLists(ListNode[] lists, int start, int end) {
if (start == end) {
return lists[start];
}
if (start > end) {
return null;
}
int mid = (start + end) >> 1;
return merge(mergeLists(lists, start, mid), mergeLists(lists, mid + 1, end));
}
public ListNode merge(ListNode head1, ListNode head2) {
if (head1 == null || head2 == null) {
return head1 != null ? head1 : head2;
}
ListNode dummyNode = new ListNode(0);
ListNode cur = dummyNode;
while (head1 != null && head2 != null) {
if (head1.val < head2.val) {
cur.next = head1;
head1 = head1.next;
} else {
cur.next = head2;
head2 = head2.next;
}
cur = cur.next;
}
cur.next = (head1 != null ? head1 : head2);
return dummyNode.next;
}
}
Method 2. Priority queue
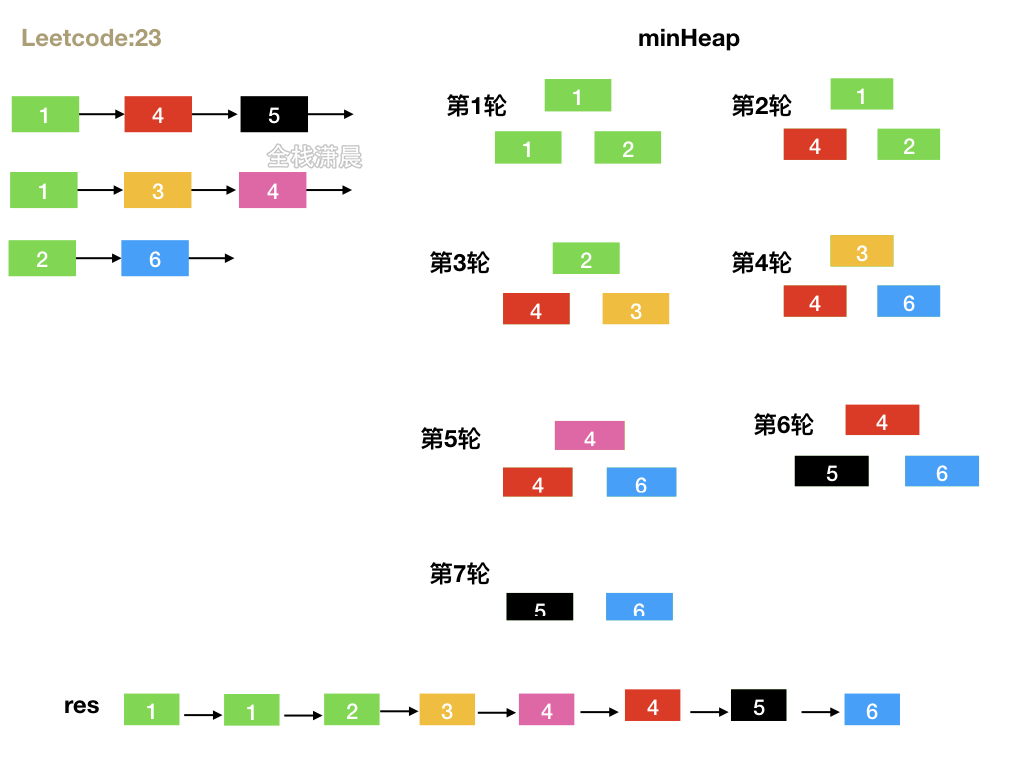
- Idea: create a new small top heap. The size of the small top heap is k. continue to add it to the small top heap from the head node of each linked list, then take out the top value of the heap, that is, the minimum value, and then continue to insert the minimum value into the small top heap in the next node of the linked list
- Complexity: the time complexity is O(kn*logk), the size of the priority queue is k, and each insertion and deletion is O(logk). There are a total of k * n nodes, and each node is inserted and deleted once, so the total complexity is O(kn*logk). The spatial complexity is O(k), that is, the size of the priority queue
js:
class Heap { constructor(comparator = (a, b) => a - b, data = []) { this.data = data; this.comparator = comparator;//Comparator this.heapify()// Heap} heapify() {if (this. Size() < 2) return; for (let I = math. Floor (this. Size() / 2) - 1; I > = 0; I --) {this. Bubbledown (I); / / bubbledown operation}} peek() {if (this. Size() = = 0) return null; return this. Data [0]; / / view the heap top} offer (value) {this. Data. Push (value) ; / / add the array this.bubbleUp(this.size() - 1); / / adjust the position of the added element in the small top heap} poll() {if (this. Size() = = 0) {return null;} const result = this. Data [0]; const last = this. Data. Pop(); if (this. Size()! = = 0) {this. Data [0] =Last; / / exchange the first and last element this.bubbleDown(0);//bubbleDown operation} return result;} bubbleup (index) {while (index > 0) {const parentindex = (index - 1) >>1; / / the location of the parent node / / if the current element is smaller than the element of the parent node, exchange the location of the current node and the parent node if (this. Comparator (this. Data [index], this. Data [parentindex]) < 0) {this. Swap (index, parentindex) ; / / exchange the position between yourself and the parent node. index = parentIndex; / / constantly take the parent node for comparison} else {break; / / if the current element is larger than the element of the parent node, you don't need to process}}} bubbledown (index) {const lastindex = this. Size() - 1; / / the position of the last node while (true) {const leftindex = index * 2 + 1; / / the location of the left node const rightIndex = index * 2 + 2; / / the location of the right node let FindIndex = index; / / the location of the bubbledown node / / find the node with a small value in the left and right nodes if (leftindex < = lastindex & & this. Comparator (this. Data [leftIndex], this.data[findIndex]) < 0 ) { findIndex = leftIndex; } if ( rightIndex <= lastIndex && this.comparator(this.data[rightIndex], this.data[findIndex]) < 0 ) { findIndex = rightIndex; } if (index !== findIndex) {this. Swap (index, FindIndex); / / exchange the current element and the index with small value in the left and right nodes = FindIndex;} else {break;}}} swap (index1, index2) {/ / exchange the positions of the two elements in the heap [this. Data [index1], this. Data [index2]] = [this. Data [index2], this. Data [index1]] ;} size() {return this. Data. Length;}} var mergeklists = function (lists) {const res = new listnode (0); let P = res; const H = new heap (comparator = (a, b) = > a.val - b.val); lists.foreach (L = > {/ / insert the first node of each linked list if (L) h.offer (L);}) while (h.size()) {/ / const n = h.poll () ; / / get the minimum value p.next = n; / / add the minimum value to P's next, p = p.next; / / move the P node if(n.next) h.offer(n.next); / / insert the next node of the minimum node} return res.next;};
java:
class Solution {
class Status implements Comparable<Status> {
int val;
ListNode ptr;
Status(int val, ListNode ptr) {
this.val = val;
this.ptr = ptr;
}
public int compareTo(Status status2) {
return this.val - status2.val;
}
}
PriorityQueue<Status> h = new PriorityQueue<Status>();
public ListNode mergeKLists(ListNode[] lists) {
for (ListNode node: lists) {
if (node != null) {
h.offer(new Status(node.val, node));
}
}
ListNode res = new ListNode(0);
ListNode p = res;
while (!h.isEmpty()) {
Status n = h.poll();
p.next = n.ptr;
p = p.next;
if (n.ptr.next != null) {
h.offer(new Status(n.ptr.next.val, n.ptr.next));
}
}
return res.next;
}
}
347. Top K high frequency elements (medium)
Method 1: priority queue

- Idea: loop the array and add the small top heap. When the size of the heap exceeds K, it will be out of the heap. After the loop is completed, all elements in the heap are the first k digits
- Complexity: time complexity O(nlogk), n cycles, and each heap operation is O(logk). Space complexity O(k),
js:
class Heap {
constructor(comparator = (a, b) => a - b, data = []) {
this.data = data;
this.comparator = comparator;//comparator
this.heapify();//Heap
}
heapify() {
if (this.size() < 2) return;
for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
this.bubbleDown(i);//bubbleDown operation
}
}
peek() {
if (this.size() === 0) return null;
return this.data[0];//View the top of the heap
}
offer(value) {
this.data.push(value);//Add array
this.bubbleUp(this.size() - 1);//Adjust the position of the added elements in the small top heap
}
poll() {
if (this.size() === 0) {
return null;
}
const result = this.data[0];
const last = this.data.pop();
if (this.size() !== 0) {
this.data[0] = last;//Swap the first and last elements
this.bubbleDown(0);//bubbleDown operation
}
return result;
}
bubbleUp(index) {
while (index > 0) {
const parentIndex = (index - 1) >> 1;//Location of parent node
//If the current element is smaller than the element of the parent node, the positions of the current node and the parent node are exchanged
if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
this.swap(index, parentIndex);//Swap the location of yourself and the parent node
index = parentIndex;//Continuously take up the parent node for comparison
} else {
break;//If the current element is larger than the element of the parent node, it does not need to be processed
}
}
}
bubbleDown(index) {
const lastIndex = this.size() - 1;//Location of the last node
while (true) {
const leftIndex = index * 2 + 1;//Location of left node
const rightIndex = index * 2 + 2;//Location of the right node
let findIndex = index;//Location of the bubbleDown node
//Find the node with small value in the left and right nodes
if (
leftIndex <= lastIndex &&
this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
) {
findIndex = leftIndex;
}
if (
rightIndex <= lastIndex &&
this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
) {
findIndex = rightIndex;
}
if (index !== findIndex) {
this.swap(index, findIndex);//Swap the current element and the small value in the left and right nodes
index = findIndex;
} else {
break;
}
}
}
swap(index1, index2) {//Swap the positions of the two elements in the heap
[this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
}
size() {
return this.data.length;
}
}
var topKFrequent = function (nums, k) {
const map = new Map();
for (const num of nums) {//Statistical frequency
map.set(num, (map.get(num) || 0) + 1);
}
//Create small top heap
const priorityQueue = new Heap((a, b) => a[1] - b[1]);
//entry is an array with a length of 2. key is stored at position 0 and value is stored at position 1
for (const entry of map.entries()) {
priorityQueue.offer(entry);//Add heap
if (priorityQueue.size() > k) {//When the size of the heap exceeds k, it is out of the heap
priorityQueue.poll();
}
}
const ret = [];
for (let i = priorityQueue.size() - 1; i >= 0; i--) {//Take out the first k large number
ret[i] = priorityQueue.poll()[0];
}
return ret;
};
java:
class Solution {
public int[] topKFrequent(int[] nums, int k) {
int[] ret = new int[k];
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
map.put(num, map.getOrDefault(num, 0) + 1);
}
Set<Map.Entry<Integer, Integer>> entries = map.entrySet();
PriorityQueue<Map.Entry<Integer, Integer>> priorityQueue = new PriorityQueue<>((o1, o2) -> o1.getValue() - o2.getValue());
for (Map.Entry<Integer, Integer> entry : entries) {
priorityQueue.offer(entry);
if (priorityQueue.size() > k) {
priorityQueue.poll();
}
}
for (int i = k - 1; i >= 0; i--) {
ret[i] = priorityQueue.poll().getKey();
}
return ret;
}
}
692. Top K high frequency words(medium)
Method 1: sort
js:
var topKFrequent = function (words, k) {
const map = {};
words.forEach(v => map[v] = (map[v] || 0) + 1);
const keys = Object.keys(map).sort((a, b) => map[b] - map[a] || a.localeCompare(b))
return keys.slice(0, k);
};
Method 2: heap
js:
class Heap {
constructor(comparator = (a, b) => a - b, data = []) {
this.data = data;
this.comparator = comparator;//comparator
this.heapify();//Heap
}
heapify() {
if (this.size() < 2) return;
for (let i = Math.floor(this.size()/2)-1; i >= 0; i--) {
this.bubbleDown(i);//bubbleDown operation
}
}
peek() {
if (this.size() === 0) return null;
return this.data[0];//View the top of the heap
}
offer(value) {
this.data.push(value);//Add array
this.bubbleUp(this.size() - 1);//Adjust the position of the added elements in the small top heap
}
poll() {
if (this.size() === 0) {
return null;
}
const result = this.data[0];
const last = this.data.pop();
if (this.size() !== 0) {
this.data[0] = last;//Swap the first and last elements
this.bubbleDown(0);//bubbleDown operation
}
return result;
}
bubbleUp(index) {
while (index > 0) {
const parentIndex = (index - 1) >> 1;//Location of parent node
//If the current element is smaller than the element of the parent node, the positions of the current node and the parent node are exchanged
if (this.comparator(this.data[index], this.data[parentIndex]) < 0) {
this.swap(index, parentIndex);//Swap the location of yourself and the parent node
index = parentIndex;//Continuously take up the parent node for comparison
} else {
break;//If the current element is larger than the element of the parent node, it does not need to be processed
}
}
}
bubbleDown(index) {
const lastIndex = this.size() - 1;//Location of the last node
while (true) {
const leftIndex = index * 2 + 1;//Location of left node
const rightIndex = index * 2 + 2;//Location of the right node
let findIndex = index;//Location of the bubbleDown node
//Find the node with small value in the left and right nodes
if (
leftIndex <= lastIndex &&
this.comparator(this.data[leftIndex], this.data[findIndex]) < 0
) {
findIndex = leftIndex;
}
if (
rightIndex <= lastIndex &&
this.comparator(this.data[rightIndex], this.data[findIndex]) < 0
) {
findIndex = rightIndex;
}
if (index !== findIndex) {
this.swap(index, findIndex);//Swap the current element and the small value in the left and right nodes
index = findIndex;
} else {
break;
}
}
}
swap(index1, index2) {//Swap the positions of the two elements in the heap
[this.data[index1], this.data[index2]] = [this.data[index2], this.data[index1]];
}
size() {
return this.data.length;
}
}
var topKFrequent = function (nums, k) {
const map = new Map();
for (const num of nums) {//Statistical frequency
map.set(num, (map.get(num) || 0) + 1);
}
//Create small top heap
const priorityQueue = new Heap((a, b) => {
return a[1] === b[1] ? b[0].localeCompare(a[0]) : a[1] - b[1]
});
//entry is an array with a length of 2. key is stored at position 0 and value is stored at position 1
for (const entry of map.entries()) {
priorityQueue.offer(entry);//Add heap
if (priorityQueue.size() > k) {//When the size of the heap exceeds k, it is out of the heap
priorityQueue.poll();
}
}
const ret = [];
for (let i = priorityQueue.size() - 1; i >= 0; i--) {//Take out the first k large number
ret[i] = priorityQueue.poll()[0];
}
return ret;
};
933. Number of recent requests (easy)
- Idea: add the request to the queue. If the request time of the queue header element is beyond [t-3000,t], it will continue to leave the queue
- Complexity: time complexity O(q), q is the number of ping s. Space complexity O(w), w is the maximum number of elements in the queue
js:
var RecentCounter = function() {
this.queue = []
};
RecentCounter.prototype.ping = function(t) {
this.queue.push(t);//New request to join the team
const time = t-3000;//Calculate the time before 3000ms
while(this.queue[0] < time){//If the time requested by the queue head element is outside [t-3000,t], it will continue to leave the queue
this.queue.shift();
}
return this.queue.length;//In the [t-3000,t] interval, the remaining elements in the queue are the number of requests that meet the requirements
};
java:
class RecentCounter {
Queue<Integer> q;
public RecentCounter() {
q = new LinkedList();
}
public int ping(int t) {
q.add(t);
while (q.peek() < t - 3000)
q.poll();
return q.size();
}
}
622. Design cyclic queue (medium)
- Complexity: time complexity O(1), space complexity O(k)
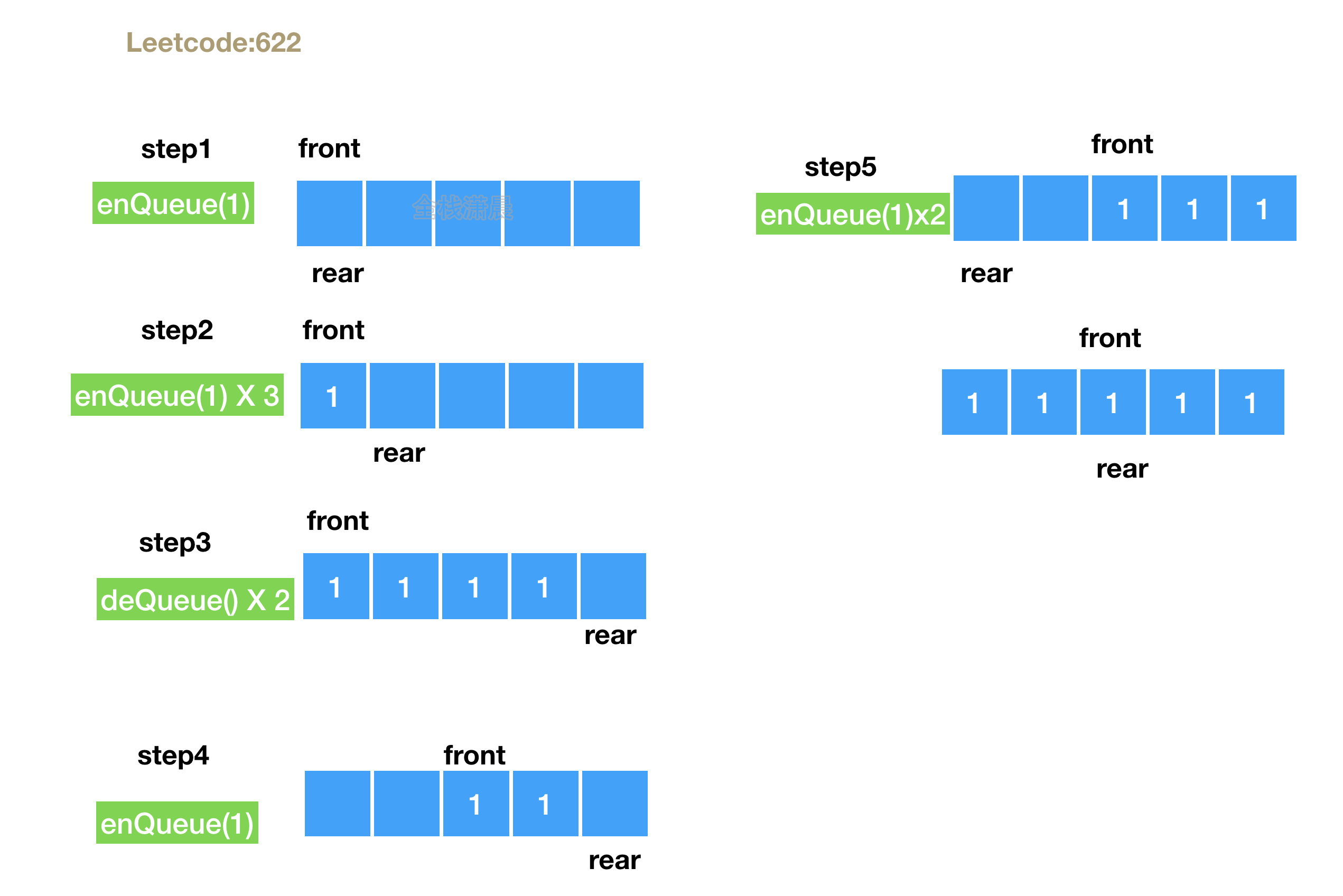
js:
var MyCircularQueue = function(k) {
this.front = 0
this.rear = 0
this.max = k
this.list = Array(k)
};
MyCircularQueue.prototype.enQueue = function(value) {
if(this.isFull()) {
return false
} else {
this.list[this.rear] = value
this.rear = (this.rear + 1) % this.max
return true
}
};
MyCircularQueue.prototype.deQueue = function() {
let v = this.list[this.front]
this.list[this.front] = undefined
if(v !== undefined ) {
this.front = (this.front + 1) % this.max
return true
} else {
return false
}
};
MyCircularQueue.prototype.Front = function() {
if(this.list[this.front] === undefined) {
return -1
} else {
return this.list[this.front]
}
};
MyCircularQueue.prototype.Rear = function() {
let rear = this.rear - 1
if(this.list[rear < 0 ? this.max - 1 : rear] === undefined) {
return -1
} else {
return this.list[rear < 0 ? this.max - 1 : rear]
}
};
MyCircularQueue.prototype.isEmpty = function() {
return this.front === this.rear && !this.list[this.front]
};
MyCircularQueue.prototype.isFull = function() {
return (this.front === this.rear) && !!this.list[this.front]
};