70. Hierarchical traversal of binary tree II
Give a binary tree and return its node values to traverse from bottom to top (traverse from the layer where the leaf node is located to the layer where the root node is located, and then traverse from left to right layer by layer)


bfs can do bugfree.
from typing import (
List,
)
from lintcode import (
TreeNode,
)
"""
Definition of TreeNode:
class TreeNode:
def __init__(self, val):
self.val = val
self.left, self.right = None, None
"""
from collections import deque
class Solution:
"""
@param root: A tree
@return: buttom-up level order a list of lists of integer
"""
def level_order_bottom(self, root: TreeNode) -> List[List[int]]:
# write your code here
if not root:
return []
que = deque([root])
tmp = []
while que:
li = []
for _ in range(len(que)):
node = que.popleft()
li.append(node.val)
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
tmp.append(li)
return tmp[::-1]
1807 Fibonacci sequence is simple
describe
Find the nth number in Fibonacci sequence.
The so-called Fibonacci sequence refers to:
The first two numbers are 0 and 1.
The i-th number is the sum of the i-1 st number and the i-2 nd number.
The first 10 numbers of Fibonacci series are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ...

Recursive version:
def fibonacci(self, n: int) -> int:
# write your code here
if n == 1 or n == 2:
return n - 1
return self.fibonacci(n - 1) + self.fibonacci(n - 2)
Non recursive version:
def fibonacci(self, n: int) -> int:
# write your code here
a, b = 0, 1
for _ in range(2, n):
a, b = b, a + b
return b
242. Convert binary tree into linked list according to hierarchy
For a binary tree, design an algorithm to establish a linked list for the nodes of each layer. In other words, if a binary tree has d layers, you need to create D linked lists.

"""
Definition of TreeNode:
class TreeNode:
def __init__(self, val):
this.val = val
this.left, this.right = None, None
Definition for singly-linked list.
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
"""
from collections import deque
class Solution:
# @param {TreeNode} root the root of binary tree
# @return {ListNode[]} a lists of linked list
def binaryTreeToLists(self, root):
# Write your code here
if not root: return []
que = deque([root])
res = []
while que:
dummy = ListNode(-1)
head = dummy
for _ in range(len(que)):
node = que.popleft()
head.next = ListNode(node.val)
head = head.next
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
res.append(dummy.next)
return res
95. Verify binary lookup tree
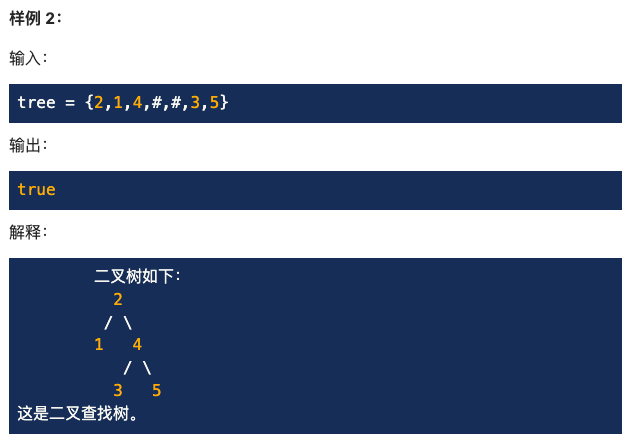
Given a binary tree, judge whether it is a legal binary search tree (BST)
A BST is defined as:
The value in the left subtree of a node must be strictly less than the value of the node.
The value in the right subtree of a node must be strictly greater than the value of the node.
The left and right subtrees must also be binary search trees.
The tree of a node is also a binary lookup tree.

Didn't write it out, didn't guarantee that the values on the left are smaller than those on the compartment.
from lintcode import (
TreeNode,
)
"""
Definition of TreeNode:
class TreeNode:
def __init__(self, val):
self.val = val
self.left, self.right = None, None
"""
class Solution:
"""
@param root: The root of binary tree.
@return: True if the binary tree is BST, or false
"""
def is_valid_b_s_t(self, root: TreeNode) -> bool:
# write your code here
if not root:
return True
elif not root.left and not root.right:
return True
bool1, bool2 = True, True
if root.left:
if root.left.val >= root.val:
return False
bool1 = self.is_valid_b_s_t(root.left)
if root.right:
if root.right.val <= root.val:
return False
bool2 = self.is_valid_b_s_t(root.right)
return bool1 and bool2
Remember how to do it before. It's the method told by the teacher. Traverse them to see if they are in ascending order.
def isValidBST(self, root):
# write your code here
res = []
self.BST_traverse(root, res)
for i in range(1, len(res)):
if res[i] <= res[i - 1]:
return False
return True
def BST_traverse(self, root, res):
if not root: return
self.BST_traverse(root.left, res)
res.append(root.val)
self.BST_traverse(root.right, res)
155. Minimum depth of binary tree
Given a binary tree, find its minimum depth.
The minimum depth of the binary tree is the number of nodes on the shortest path from the root node to the nearest leaf node.


BFS version:
from lintcode import (
TreeNode,
)
"""
Definition of TreeNode:
class TreeNode:
def __init__(self, val):
self.val = val
self.left, self.right = None, None
"""
from collections import deque
class Solution:
"""
@param root: The root of binary tree
@return: An integer
"""
def min_depth(self, root: TreeNode) -> int:
# write your code here
if not root:
return 0
que = deque([root])
depth = 1
while que:
for _ in range(len(que)):
node = que.popleft()
if not node.left and not node.right:
return depth
if node.left:
que.append(node.left)
if node.right:
que.append(node.right)
depth += 1
DFS version:
from lintcode import (
TreeNode,
)
"""
Definition of TreeNode:
class TreeNode:
def __init__(self, val):
self.val = val
self.left, self.right = None, None
"""
class Solution:
"""
@param root: The root of binary tree
@return: An integer
"""
def min_depth(self, root: TreeNode) -> int:
# write your code here
if not root:
return 0
depth = 1
dep = self.dfs(root, depth)
return dep
def dfs(self, root, depth):
if not root.left and not root.right:
return depth
left_dep, right_dep = float('inf'), float('inf')
if root.left:
left_dep = self.dfs(root.left, depth + 1)
if root.right:
right_dep = self.dfs(root.right, depth + 1)
return min(left_dep, right_dep)
The following is the official answer. I feel I can't think of it
def minDepth(self, root):
if root is None:
return 0
leftDepth = self.minDepth(root.left)
rightDepth = self.minDepth(root.right)
# When the left or right subtree is empty, the minimum depth depends on another subtree
if leftDepth == 0 or rightDepth == 0:
return leftDepth + rightDepth + 1
return min(leftDepth, rightDepth) + 1