502. IPO
Given k,w,profits Array and capital Array. k Indicates the maximum number of tasks that can be completed. w Is the initial capital. profits Is the benefit of each task. capital This is the initial funding required to start this task. After completing one task at a time, add the income to the capital. Ask how much capital can be achieved at most.
Greedy. Use priority queue. Select the tasks that can be started each time to get the most benefit.
class Solution {
public:
struct pc{
int profits;
int capital;
pc(int u,int v):profits(u),capital(v){}
bool operator < (const Solution::pc &b) const {
return profits < b.profits;
}
};
struct cmp{
bool operator()(struct pc &a,struct pc &b)const {
if(a.capital != b.capital) return a.capital < b.capital;
return a.profits > b.profits;
}
};
int findMaximizedCapital(int k, int W, vector<int>& Profits, vector<int>& Capital) {
vector<pc> v;
for(int i = 0;i < Profits.size(); ++i){
v.push_back(pc(Profits[i],Capital[i]));
}
sort(v.begin(),v.end(),cmp());
priority_queue<pc> Q;
int pos = 0;
while(pos < v.size() && v[pos].capital <= W){
Q.push(v[pos++]);
}
while(!Q.empty() && k--){
pc u = Q.top(); Q.pop();
W += u.profits;
while(pos < v.size() && v[pos].capital <= W){
Q.push(v[pos++]);
}
}
return W;
}
};514. Freedom Trail
Given a cipher ring, there are some lowercase letters on the ring. The door can only be opened by turning the ring and then pressing the button to enter the correct password. The password is a string. The characters on the ring are given as a string, arranged clockwise. It can rotate counterclockwise and clockwise, turning one grid meter one step. Press the button to enter the character at position 0 and count one step. Ask at least how many steps you can enter the password.
Dynamic programming. set up dp[i][j]express key from i At the end, the character on the ring is now at j At least steps are required to enter the password. Then turn to key[i]Character position k,be dp[i][j] = min{dp[i + 1][k]} + 1. and k Just enumerate the left and right sums closest to the current position key[i]Equal position is enough(Because it is lowercase, this can be in O(32 * ring.length())The time is calculated in advance. Then, because dp[i]Only dp[i + 1]So you can scroll the array and reduce the space complexity to O(Ring.size() + Key.size())
class Solution {
public:
int findRotateSteps(string ring, string key) {
int n = ring.size();
int m = key.size();
if(m == 0) return 0;
vector<vector<int> > left(n,vector<int>(26)),right(n,vector<int>(26));
vector<int> leftpos(26,-1),rightpos(26,-1);
for(int i = 0;i < n; ++i){
leftpos[ring[i] - 'a'] = i;
rightpos[ring[n - i - 1] - 'a'] = n - i - 1;
}
for(int i = 0;i < n; ++i){
leftpos[ring[i] - 'a'] = i;
rightpos[ring[n - i - 1] - 'a'] = n - i - 1;
for(int j = 0;j < 26; ++j){
left[i][j] = leftpos[j];
right[n - i - 1][j] = rightpos[j];
}
}
vector<vector<int> > dp(2,vector<int>(n,0));
for(int i = m - 1;i >= 0; --i){
int c = key[i] - 'a';
for(int j = 0;j < n; ++j){
int L = left[j][c];
int R = right[j][c];
dp[i & 1][j] = min((j - L + n) % n + dp[1 - i & 1][L],(R - j + n) % n + dp[1 - i & 1][R]) + 1;
}
}
return dp[0][0];
}
};517. Super Washing Machines
Given N Pile coins(May be empty),You can choose at any time m Pile, take one from each pile and put it in the next pile. Ask at least how many times you can make all piles of coins the same.
Solution: dp[i]Indicates the first 0 to i How many times can the stack put the excess coins to the right at least, and all but the last one reach the target value. dp[i + 1] = dp[i] + L +R,among L and R Respectively from i+1 The number of coins taken by the pile to the left and right.
class Solution {
public:
int findMinMoves(vector<int>& machines) {
int n = machines.size();
if(n <= 1) return 0;
int tot = 0,ans = 0;
for(int i = 0;i < n; ++i) tot += machines[i];
if(tot % n) return -1;
int ave = tot / n;
machines.push_back(ave);
tot = 0;
tot = machines[0] - ave;
for(int i = 0;i < n; ++i){
if(tot >= 0)
ans = max(tot,ans);
else{
ans = max(ans,max(0,machines[i + 1] + tot - ave) - tot);
}
tot += machines[i + 1] - ave;
machines[i + 1] += tot;
}
return ans;
}
};546. Remove Boxes
Given a sequence of integers, each number represents a color. Several consecutive segments of the same color can be taken away at a time(Count Reg k),get k*k Score. Ask how to get the maximum score when the sequence is taken.
Dynamic programming. Because continuous ones must be taken together, they should be merged first. set up dp[i][j][k]Indicates the slave location i To position j,What's left in front k Gehe i The same color location, then either i Merge with the previous one, take it away, or stay together, and merge with the next one. The answer is dp[0][n - 1][0].
//vector will overrun memory
class Solution {
public:
void merge(vector<int>& boxes,int n,vector<int>&color,vector<int>&length){
boxes.push_back(-1);
int curLength = 0;
for(int i = 0;i < n; ++i){
++curLength;
if(boxes[i] == boxes[i + 1]) continue;
length.push_back(curLength);
color.push_back(boxes[i]);
curLength = 0;
}
}
int removeBoxes(vector<int>& boxes) {
int n = boxes.size();
if(n <= 1) return n;
vector<int> color,length;
merge(boxes,n,color,length);
n = color.size();
if(n == 1) return length[0] * length[0];
//vector<vector<vector<int>>> dp(n,vector<vector<int>>(n,vector<int>(boxes.size(),0)));
int dp[100][100][100] = {0};
return dfs(dp,color,length,0,n - 1,0);
}
int dfs(int dp[100][100][100],const vector<int>& color,vector<int>&length,int i,int j,int k){
if(i > j) return 0;
if(i == j) return (k + length[i]) * (k + length[i]);
int &res = dp[i][j][k];
if(res) return res;
res = dfs(dp,color,length,i + 1,j,0) + (k + length[i]) * (k + length[i]);
for(int p = i + 1;p <= j; ++p){
if(color[p] != color[i]) continue;
res = max(res, dfs(dp, color,length, i + 1, p - 1, 0) + dfs(dp, color,length, p, j, k + length[i]));
}
return res;
}
};
552. Student Attendance Record II
Given three characters(A,P,L)Give a number n,Ask length n How many strings are composed of these three characters. The restriction is one of them. There can only be one(A),There is also a maximum of two consecutive( L),There is no limit to the remaining one(P).
Solution: dp[i][j][k]Indicates that the length is i,A Whether it has occurred, and the end is continuous L The number of is k Number of strings. Then transfer. because dp[i]Only dp[i - 1]Therefore, a scrolling array can be used.
class Solution {
public:
const long long MOD = 1E9 + 7;
int checkRecord(int n) {
long long dp[2][2][3] = {0LL};
dp[0][0][0] = 1LL;
for(int i = 1;i <= n; ++i){
for(int k = 0;k < 3; ++k){
if(k > 0){
dp[i&1][0][k] = dp[1 - i&1][0][k - 1];
dp[i&1][1][k] = dp[1 - i&1][1][k - 1];
}
else{
dp[i&1][0][k] = dp[1 - i&1][0][0] + dp[1 - i&1][0][1] + dp[1 - i&1][0][2];
dp[i&1][1][k] = dp[1 - i&1][1][0] + dp[1 - i&1][1][1] + dp[1 - i&1][1][2] +
dp[i&1][0][k];
}
dp[i&1][0][k] %= MOD;
dp[i&1][1][k] %= MOD;
}
}
return (dp[n&1][0][0] + dp[n&1][0][1] + dp[n&1][0][2] + dp[n&1][1][0] + dp[n&1][1][1] + dp[n&1][1][2]) % MOD;
}
};564. Find the Closest Palindrome
Given a numeric string, determine the palindrome string closest to it. If two are as close, output the smaller one.
If the first half of the palindrome of the string is not the smallest, then take the first half of the palindrome of the string itself. If it is a palindrome string, subtract 1 from the first half and add 1 to construct a palindrome string. Recently, it must be one of these two. Obviously, then there is the problem of details.
class Solution {
public:
bool g(string a,string b){ //a > b? true: false;
if(a == "inf") return true;
if(b == "inf") return false;
if(a.length() > b.length()) return true;
if(a.length() < b.length()) return false;
for(int i = 0;i < a.length(); ++i){
if(a[i] > b[i]) return true;
if(a[i] < b[i]) return false;
}
return false;
}
string dis(string a,string b){
if(a == b) return "inf";
if(g(a,b)) swap(a,b);
a = string(b.length() - a.length(),'0') + a;
char tmp = 0;
string s = "";
int i = 0;
for(int i = a.length() - 1;i >= 0; --i){
char t = b[i] - a[i] - tmp;
if(t < 0) tmp = 1, t += 10;
else tmp = 0;
s = char('0' + t) + s;
}
int pos = 0 ;
while(pos < s.length() && s[pos] == '0') ++pos;
s = s.substr(pos);
return s == string("0") ? "inf":s;
}
string minor(string s){
int mid = (s.length() + 1) / 2;
for(int i = mid; i < s.length() ; ++i)
s[i] = s[s.length() - 1 - i];
return s;
}
string nearestPalindromic(string s) {
int pos = 0;
while(pos < s.length() - 1 && s[pos] == '0') ++pos;
s = s.substr(pos);
int n = s.size();
if(n <= 1){
cout<<"true"<<endl;
if(s == "") return "0";
if(s == "0") return "1";
cout<<"noew"<<(s[0] - 1)<<endl;
return string("") + char(s[0] - 1);
}
string s1 = minor(s);
string diff1 = dis(s,s1);
int mid = (s.length() - 1) / 2;
string s2 = s;
while(mid >= 0 && s2[mid] == '0'){
s2[mid] = '9';
--mid;
}
if(mid == 0 && *(s2.begin()) == '1'){
s2.erase(s2.begin());
s2[(s2.length() - 1) / 2] = '9'; //this is because it's the closer one
}
else
s2[mid] = s2[mid] - 1;
s2 = minor(s2);
string diff2 = dis(s,s2);
mid = (s.length() - 1) / 2;
string s3 = s;
while(mid >= 0 && s3[mid] == '9'){
s3[mid] = '0';
--mid;
}
if(mid < 0)
s3 = "1" + s3;
else
s3[mid] = s3[mid] + 1;
s3 = minor(s3);
string diff3 = dis(s,s3);
if(!g(diff2,diff1) && !g(diff2,diff3)) return s2;
if(!g(diff1,diff2) && !g(diff1,diff3)) return s1;
return s3;
}
};587. Erect the Fence
The convex hull is a whole point, which may be repeated or degenerated into a straight line. Start from the far left and output counterclockwise.
Solution: Graham scanning
/**
* Definition for a point.
* struct Point {
* int x;
* int y;
* Point() : x(0), y(0) {}
* Point(int a, int b) : x(a), y(b) {}
* };
*/
Point operator-(Point &a, Point &b) {
int x = a.x - b.x;
int y = a.y - b.y;
return Point(x,y);
}
class Solution {
public:
struct cmp{
bool operator()(const Point &a, const Point &b){
if(a.x == b.x) return a.y < b.y;
return a.x < b.x;
}
};
bool eq(const Point &a, const Point &b){
return a.x == b.x && a.y == b.y;
}
int cross(Point &a,Point &b){
return a.x * b.y - a.y * b.x;
}
vector<int> convexHull(vector<Point>& points){
int n = points.size();
vector<int> S(n,0);
int end = 0;
for(int i = 1;i < n; ++i){
if(end == 0){
S[++end] = i;
continue;
}
int top = S[end];
int pre = S[end - 1];
Point v1 = points[i] - points[pre];
Point v2 = points[top] - points[pre];
if(cross(v1,v2) > 0){
--end;
--i;
}else{
S[++end] = i;
}
}
vector<int> down(S.begin(),S.begin() + end + 1);
if(down.size() == points.size()) return down;
S[0] = n - 1; end = 0;
for(int i = n - 2;i >= 0; --i){
if(end == 0){
S[++end] = i;
continue;
}
int top = S[end];
int pre = S[end - 1];
Point v1 = points[i] - points[pre];
Point v2 = points[top] - points[pre];
if(cross(v1,v2) > 0){
--end;
++i;
}else{
S[++end] = i;
}
}
vector<int>up(S.begin() + 1,S.begin() + end);
down.insert(down.end(),up.begin(),up.end());
return down;
}
/*
int gcd(int a,int b){
return b == 0 ? a : gcd(b, a % b);
}
bool inaLine(vector<Point>& points){
int pos = 1;
while(pos < points.size() && points[pos].x == points[0].x && points[pos].y == points[0].y) ++pos;
if(pos == points.size()) return true;
Point tmp = points[pos] - points[0];
int x = tmp.x,y = tmp.y;
int d = gcd(x,y);
x /= d; y /= d;
for(int i = 1;i < points.size(); ++i){
int px = points[i].x - points[0].x, py = points[i].y - points[0].y;
if(px == 0 && py == 0) continue;
d = gcd(px,py);
px /= d; py /= d;
if(x != px || y != py) return false;
}
return true;
}
*/
vector<Point> outerTrees(vector<Point>& points) {
if(points.size() <= 1) return points;
sort(points.begin(),points.end(),cmp()); //left to right ,down to up
//if(inaLine(points)) return points;
vector<int> convex = convexHull(points);
vector<Point> ans;
for(auto pos:convex) ans.push_back(points[pos]);
return ans;
}
};600. Non-negative Integers without Consecutive Ones
Give a number n,Ask how many nonnegative numbers are smaller than it and the binary has no continuous 1.
Note that the binary length is k Is a nonnegative number without a continuous 1 Fibonacci Count. Then, for a n,We calculate the numbers with the same prefix and add them up. If it is, add it. Another approach is dynamic programming. dp[i][j]Before representation i position,The last one is j And not greater than num Number of prefixes.
class Solution {
public:
int findIntegers(int num) {
int fib[31];
fib[0] = 1;
fib[1] = 2;
for (int i = 2; i < 32; ++i)
fib[i] = fib[i - 1] + fib[i - 2];
int ans = 0, k = 30, pre_bit = 0;
for(int k = 30;k >= 0; --k) {
if (num & (1 << k)) {
ans += fib[k];
if (pre_bit) return ans;
pre_bit = 1;
}else
pre_bit = 0;
}
return ans + 1;
}
};
Dynamic programming solution, compressed space:
public class Solution {
public int findIntegers(int num) {
//one:all bit before cur is less than num and no continues 1 and cur bit is at one;
//zero:all bit before cur is less than num and no continues 1 and cur bit is at zero;
int one=0,zero=0,temp;
boolean isNum=true;
for(int i=31;i>=0;i--){
temp=zero;
zero+=one;
one=temp;
if(isNum&&((num>>i)&1)==1){
zero+=1;
}
if(((num>>i)&1)==1&&((num>>i+1)&1)==1){
isNum=false;
}
}
return one+zero+(isNum?1:0);
}
}629. K Inverse Pairs Array
Given n,k. Question by 1 ~n The reverse order pair in the sequence is k How many situations are there
Dynamic programming. set up dp[i][j]Yes, there is 1 in front~i + 1 Sequence of,Reverse order pair j How many are there. that dp[i][j]
Can be i + 1 Recursion at the location. dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1] + ... dp[i - 1][max(0,j - i)]
And each pre calculation, so the time complexity is O(nk)
class Solution {
public:
const int MOD = 1E9 + 7;
int getsum(int i,int j, vector<int> &sum)const {
int pre = max(j - i,0) - 1;
if(pre < 0) return sum[j];
else return sum[j] - sum[pre];
}
int kInversePairs(int n, int k) {
if(k == 0) return 1;
vector<int> dp(k + 1,0);
vector<int> sum(k + 1,1);
dp[0] = 1;
for(int i= 0;i < n; ++i){
for(int j = 1;j <= k; ++j){
dp[j] = (getsum(i,j,sum) % MOD + MOD) % MOD;
}
for(int j = 1;j <= k; ++j) sum[j] = (sum[j - 1] + dp[j]) % MOD;
}
return dp[k];
}
};630. Course Schedule III
Give some courses to(The required time, the latest end time) is given. Courses cannot overlap. Ask how many courses can be arranged at most.
Greedy. First, sort the courses according to the latest end time from small to large. Then arrange one by one. If you can arrange it, put it in. If you can't arrange, remove the front(Including yourself)One that takes the most time. This must be the best. Because for the former i If this is the best way to do things, then for the second i+1 One, this is certainly the best, otherwise it will lead to contradiction.
class Solution {
public:
struct cmp{
bool operator ()(vector<int> &a, vector<int>&b){
return a[1] < b[1];
}
};
struct cmp2{
bool operator ()(pair<int,int> &a,pair<int,int> &b){
return a.first < b.first;
}
};
int scheduleCourse(vector<vector<int>>& courses) {
sort(courses.begin(),courses.end(),cmp());
priority_queue<pair<int,int> ,vector<pair<int,int>>, cmp2>Q;
int endTime = 0;
for(int i = 0;i < courses.size(); ++i){
Q.push(make_pair(courses[i][0],courses[i][1]));
endTime += courses[i][0];
if(endTime > courses[i][1]){
endTime -= Q.top().first;
Q.pop();
}
}
return Q.size();
}
};632. Smallest Range
Given k individual list,each list Is an orderly int Array. Find a minimum interval so that this k Each of the arrays has at least one number in this interval.
Solution: first merge into one pair array(Value and to which it belongs list). Then double pointer traversal.
class Solution {
public:
static bool cmp(pair<int,int> &a,pair<int,int> &b){
return a.first > b.first;
}
vector<int> smallestRange(vector<vector<int>>& nums) {
vector<pair<int,int>> numpair;
int k = nums.size();
for(int i = 0;i < k; ++i){
vector<pair<int,int>> tmp;
for(auto &num:nums[i]){
tmp.push_back(make_pair(num,i));
}
numpair.resize(numpair.size() + tmp.size());
merge(numpair.rbegin() + tmp.size(),numpair.rend(),tmp.rbegin(),tmp.rend(),numpair.rbegin(),cmp);
}
vector<int> counts(k);
int visn = 0;
int a = -1,b = -1,minimumS = INT_MAX;
int pre = 0;
for(int i = 0;i < numpair.size() ; ++i){
if(++counts[numpair[i].second] == 1) ++visn;
if(visn == k){
while(counts[numpair[pre].second] > 1){
--counts[numpair[pre].second];
++pre;
}
if(numpair[i].first - numpair[pre].first < minimumS){
minimumS = numpair[i].first - numpair[pre].first;
a = numpair[pre].first;
b = numpair[i].first;
}
}
}
return vector<int>{a,b};
}
};639. Decode Ways II
Meaning: characters A-Z It can be encoded into 1 to 26. Given a string of codes, ask how many cases can be decoded. Where coding;*;Can represent 1-9 Any character in.
Dynamic programming. dp[i]Indicates the front of the encoding string i Number of types that can be decoded. Then, the status is transferred according to the category of the current character and the previous character.
class Solution {
public:
long long M = 1000000007;
int numDecodings(string s) {
int n = s.size();
if(n == 0) return 1;
vector<long long> dp(n + 1,0);
dp[0] = 1;
dp[1] = s[0] == '*'? 9 : s[0] != '0';
if(dp[1] == 0) return 0;
for(int i = 2; i <= n; ++i){
if(s[i - 2] == '1'){
if(s[i - 1] == '0') dp[i] = dp[i - 2];
else if(s[i - 1] == '*') dp[i] = 9 * dp[i - 2] + dp[i - 1] * 9;
else dp[i] = dp[i - 2] + dp[i - 1];
}else if(s[i - 2] == '2'){
if(s[i - 1] == '0') dp[i] = dp[i - 2];
else if(s[i - 1] == '*') dp[i] = 6 * dp[i - 2] + dp[i - 1] * 9;
else if(s[i - 1] <= '6' && s[i - 1] >='1') dp[i] = dp[i - 2] + dp[i - 1];
else dp[i] = dp[i - 1];
}else if(s[i - 2] == '*'){
if(s[i - 1] == '0') dp[i] = 2 * dp[i - 2];
else if(s[i - 1] == '*') dp[i] = 15 * dp[i - 2] + dp[i - 1] * 9;
else if(s[i - 1] <= '6' && s[i - 1] >= '1') dp[i] = 2 * dp[i - 2] + dp[i - 1];
else dp[i] = dp[i - 2] + dp[i - 1];
}else if(s[i - 2] > '2'){ //s[i - 2] greater than 2
if(s[i - 1] == '0') dp[i] = 0;
else if(s[i - 1] == '*')
dp[i] = 9 * dp[i - 1];
else
dp[i] = dp[i - 1];
}else{ //0
if(s[i - 1] == '0') dp[i] = 0;
else dp[i] = s[i - 1] == '*'? 9 * dp[i - 1] : dp[i - 1];
}
dp[i] = dp[i] % M;
}
return dp[n];
}
};644. Maximum Average Subarray II
Given an array and a number k. Question length must be at least k What is the maximum average value of consecutive segments of.
A simple way is to divide the answer into two parts, and then check.
(nums[i]+nums[i+1]+...+nums[j])/(j-i+1)>=x
=>nums[i]+nums[i+1]+...+nums[j]>=x*(j-i+1)
=>(nums[i]-x)+(nums[i+1]-x)+...+(nums[j]-x)>=0
Equivalent to checking whether there is a continuous segment with a length of at least k And the sum is nonnegative. That is, the largest k The sub segment sum is solved by monotone queue dynamic programming.
The complexity of the algorithm is O(nlogn). But this is not optimal. It can be achieved by using the method of computational geometry O(n).
First, calculate the prefix and P[i]. then i reach j The average value of is(P[j] - P[i - 1]) / (j - i + 1).
We see it as two points(i - 1,P[i - 1]),(j,P[j]),Obviously, the average is the slope of the line segment at their two points.
next. We maintain a lower convex hull from left to right, and each time we find the lower tangent of the convex hull. See the following diagram for details:
http://www.csie.ntnu.edu.tw/~u91029/MaximumSubarray.html
An enhanced version of this problem is to add the upper limit width. That is, add an operation to the monotonous queue
class Solution {
public:
/*
bool check(vector<int>& nums, int k,double sum){
double cur = 0,pre = 0;
for(int i = 0;i < nums.size(); ++i){
cur += nums[i] - sum;
if(i >= k) pre += nums[i - k] - sum;
if(pre < 0) cur -= pre, pre = 0;
if(i >= k - 1 && cur >= 0) return true;
}
return cur >= 0;
}
double binarySearchSolution(vector<int>& nums, int k){
double eps = 1e-6;
double left = INT_MIN,right = INT_MAX,mid;
while(right - left > eps){
mid = (left + right) / 2;
if(check(nums,k,mid)) left = mid;
else right = mid;
}
return right;
}
*/
double slope(int x,int y, vector<int> &presum){ // the slope of the x,y
return double(presum[y + 1] - presum[x]) / (y + 1 - x);
}
double convexHullSolution(vector<int>& nums, int k){
deque<int> Q;
vector<int> presum(nums.size() + 1);
presum[0] = 0;
double ans = INT_MIN;
for(int i = 0;i < nums.size(); ++i) presum[i + 1] = presum[i] + nums[i];
for(int i = k - 1;i < nums.size(); ++i){
while(Q.size() > 1 && slope(*(Q.end() - 2),Q.back() - 1,presum) >= slope(*(Q.end() - 2),i - k,presum)) Q.pop_back(); //update the convex
Q.push_back(i - k + 1);
while(Q.size() > 1 && slope(Q.front(),Q.at(1) - 1,presum) <= slope(Q.front(),i,presum)) Q.pop_front();
ans = max(ans,slope(Q.front(),i,presum));
}
return ans;
}
double findMaxAverage(vector<int>& nums, int k) {
//return binarySearchSolution(nums,k);
return convexHullSolution(nums,k);
}
};668. Kth Smallest Number in Multiplication Table
Given a multiplication table of m *n, find the number with the largest k in it
Answer: half answer mid, and then judge how many pairs are less than or equal to mid. This is known by enumerating the first multiplier. Assuming that the multiplier is i, the number less than or equal to mid is min(n, mid / i). (using double pointers may be faster, because division is time-consuming, while + + Operation -- operation is fast)
class Solution {
public:
int findKthNumber(int m, int n, int k) {
int left = 1, right = n * m;
while(left <= right){
int mid = (left + right) >> 1;
int num = (mid / n) * n;
for(int i = mid / n + 1; i <= min(m, mid); ++i){
num += mid / i;
}
if(num < k){
left = mid + 1;
}else{
right = mid - 1;
}
}
return right + 1;
}
};719. Find K-th Smallest Pair Distance
Given an array of positive integers, there is a distance (difference) between each two numbers. What is the smallest k?
Two point answer bound. Then judge the number of pairs whose distance is less than or equal to bound. If it is greater than k, it can be smaller. If it is less than or equal to K, the answer should be larger.
How to calculate the number of pairs less than or equal to bound? We calculate them one by one, sort them first, and then enumerate the small numbers, Num [i], so we only need to know how many pairs less than or equal to num [i] + bound from i + 1 to the end.
This can be obtained by two points, as long as you know that the number at the top of the row is greater than num [i] + bound.
But there is a better way. Note that num [i] is increasing. If we know num [i] + bound < = num [J], then there must be num [i + 1] + bound < = num [J]. So every time we just need to look back from the result of the previous one.
class Solution {
bool check_less_than_k(vector<int> &nums,const int bound, int k){
for(int i = 0, prev_idx = 1; i < nums.size() - 1; ++i){
while(prev_idx < nums.size() && nums[prev_idx] - nums[i] <= bound) ++prev_idx;
//prev_idx = upper_bound(nums.begin() + prev_idx, nums.end(), nums[i] + bound) - nums.begin();
k -= prev_idx - i - 1;
}
return k > 0;
}
public:
int smallestDistancePair(vector<int>& nums, int k) {
sort(nums.begin(), nums.end());
int left = 0, right = *nums.rbegin() - *nums.begin();
while(left <= right){
int mid = (right + left) >> 1;
if(check_less_than_k(nums, mid, k)){
left = mid + 1;
}else{
right = mid - 1;
}
}
return right + 1;
}
};780. Reaching Points
Given sx,sy,tx,ty. Each transformation can make sx = sx + sy or sy = sx + sy. Can I change from point (sx,sy) to point (tx,ty)
We don't change from sx,sy to tx,ty. Conversely, it's equivalent to every time tx = tx - ty or ty = ty - tx. That is, the big number minus the small one. Isn't this more phase subtraction. Simulation process plus a little optimization
class Solution {
public:
//Modified subtraction
bool reachingPoints(int sx, int sy, int tx, int ty) {
//This sentence makes TX > ty. And the result remains the same
tx += ty;
while(tx >= sx && ty >= sy) {
//Let's assume ty > TX
swap(tx, ty);
swap(sx, sy);
//The subtraction is 0. At this time, if the four are equal, it is true, otherwise it is false
//ty == sy, then ty cannot be reduced any more. So the answer is tx == sx
if(tx == ty || ty == sy) return (tx == sx && ty == sy);
//ty can only be subtracted from tx until it is equal to or less than
if(tx == sx) return (ty - sy) % tx == 0;
//Go here to explain tx > SX. tx also needs to be reduced, so ty must always reduce tx until it is less than tx, that is, modulus
ty %= tx;
}
return false;
}
};803. Bricks Falling When Hit
Given an n*m grid, position 1 means there is a brick, and 0 means there is no brick. A brick will not fall if and only if it is directly connected with the top or there are bricks that will not fall in four directions (that is, there is a path to the top in four directions). Given an array hits, it means that one position is broken each time. If there is a brick, the brick disappears. So some bricks will fall. How many bricks do you drop at a time?
Solution: it's difficult to do it directly. There's no idea. The reverse is much simpler. Consider how many bricks will be connected to the top each time you add bricks from back to front. We can do this with and search sets. Note that bricks can be added only when the bricks are broken at time I, so -- grid[i][j] is used in the code. In this way, 1 is added back every time. When it is 1, it indicates that it is currently broken.
class Solution {
int find_pa(int x, vector<int> &pa){
return x == pa[x]? x : pa[x] = find_pa(pa[x], pa);
}
public:
vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {
int n = grid.size(), m = grid[0].size();
vector<int> pa(n * m);
vector<int> nums(n * m, 1);
for(int i = 0;i < n * m; ++i) pa[i] = i;
//Delete point
for(int i = 0;i < hits.size(); ++i){
--grid[hits[i][0]][hits[i][1]];
}
int dir_x[] = {1, 0, -1, 0};
int dir_y[] = {0, 1, 0, -1};
//Initialize and query set
for(int i = 0;i < n; ++i){
for(int j = 0;j < m; ++j){
if(grid[i][j] != 1) continue;
int pa1 = find_pa(i * m + j, pa);
for(int d = 0;d < 4; ++d){
int x = i + dir_x[d];
int y = j + dir_y[d];
if(x < 0 || x >= n || y < 0 || y >= m || grid[x][y] != 1) continue;
int pa2 = find_pa(x * m + y, pa);
if(pa1 > pa2) swap(pa1, pa2);
pa[pa2] = pa1;
if(pa1 != pa2) nums[pa1] += nums[pa2];
}
}
}
//Add points, merge
vector<int> ans;
for(int i = hits.size() - 1; i >= 0; --i){
int x = hits[i][0], y = hits[i][1];
if(++grid[x][y] != 1){
ans.push_back(0);
continue;
}
int pa1 = x * m + y;
int drop_num = 0;
for(int d = 0;d < 4; ++d){
int n_x = x + dir_x[d];
int n_y = y + dir_y[d];
if(n_x < 0 || n_x >= n || n_y < 0 || n_y >= m || grid[n_x][n_y] != 1) continue;
int pa2 = find_pa(n_x * m + n_y, pa);
if(pa1 != pa2){
if(pa2 >= m)
drop_num += nums[pa2];
if(pa1 > pa2) swap(pa1, pa2);
pa[pa2] = pa1;
nums[pa1] += nums[pa2];
}
}
if(pa1 >= m) drop_num = 0;
ans.push_back(drop_num);
}
return vector<int>(ans.rbegin(), ans.rend());
}
};
805. Split Array With Same Average
Given an array A, the maximum length is 30. The number is between 0 and 10000. Divide A into two arrays B and C. Ask if you can make the average of B and C the same
Solution:
Suppose the lengths of a, B and C are len respectively_ a,len_ b,len_ c. Sum and sum respectively_ a,sum_ b,sum_ c
Then there is len first_ a = len_ b + len_ c, sum_ a = sum_ b + sum_ c
We want sum_b / len_b = sum_c / len_c has sum_b * len_c = sum_c * len_b
Will len_ c,sum_ Replace c with sum_a,sum_b,len_a,len_b get
sum_b * (len_a - len_b) = (sum_a - sum_b) * len_b. Sum obtained by simplification_ b = sum_ a * len_ b / len_ a
So we can enumerate len_b. For each len_b. We got sum_b.
The problem is, take len in A_ Can sum of B numbers get sum_b.
This can be obtained through dynamic programming. Let dp[i][s] indicate whether the sum s can be obtained by taking the number of I in A.
Suppose B is the shorter array, then len_ b <= len_ a / 2,sum_ b = sum_ a * len_ b / len_ a <= sum_ a / 2 <= 150000
dp array can also use bitset, but bool can also be used.
class Solution {
bool dp[16][150001] = {0};
public:
bool splitArraySameAverage(vector<int>& A) {
int sum_a = 0;
size_t len_a = A.size();
for(size_t i = 0;i < len_a; ++i) sum_a += A[i];
dp[0][0] = true;
for(size_t i = 0;i < len_a; ++i){
for(int k = (len_a >> 1) - 1;k >= 0; --k){
for(int s = (sum_a >> 1) - A[i]; s >= 0; --s){
if(!dp[k][s]) continue;
dp[k + 1][s + A[i]] = true;
}
}
}
for(size_t len_b = 1; len_b <= len_a >> 1; ++len_b){
if(sum_a * len_b % len_a) continue;
int sum_b = sum_a * len_b / len_a;
if(dp[len_b][sum_b]) return true;
}
return false;
}
};
862. Shortest Subarray with Sum at Least K
Given an array (there may be negative numbers), there are too many summations K>0 Shortest sub segment length of
Problem solution: it is easy to think of the dichotomy length, assuming that the length is t,Then all numbers are subtracted K/t,then check Is there a length greater than or equal to t And the sum is greater than or equal to 0. That is, the problem turns into the biggest problem k Subparagraphs and. The asymptotic time complexity is O(nlogn)
Another solution is to use monotone queue. First, we find a prefix sum pre_sum,Then we are asking pre_sum[i] - pre_sum[j] >= K in i - j least. For a k>j,If pre_sum[k] <= pre_sum[j]So obviously pre_sum[j]stay k It won't be used again because of the location k Obviously than j OK. So we maintain a monotonic queue. For the current location i,We're going to look in the monotonous queue pre_sum[i] >= pre_sum[j] + K The largest i,This can be obtained by two points.
But we note that if there is pre_sum[i] >= pre_sum[j] + K,So if there is k > i,pre_sum[k] >= pre_sum[j] + K, that k This position is not i OK. therefore j And you don't have to stay in the queue.
So the time complexity is O(n)
class Solution {
public:
int shortestSubarray(vector<int>& A, int K) {
deque<pair<int,int> > Q;
Q.emplace_back(0, -1);
int pre_sum = 0, res = INT_MAX;
for(int i = 0; i < A.size(); ++ i){
pre_sum += A[i];
while(!Q.empty() && pre_sum - Q.front().first >= K){
res = min(res, i - Q.front().second);
Q.pop_front();
}
while(!Q.empty() && Q.back().first >= pre_sum)
Q.pop_back();
Q.emplace_back(pre_sum, i);
}
return res == INT_MAX ? -1 : res;
}
};864. Shortest Path to Get All Keys
Give a two-dimensional matrix. Each position has one character@ Is the starting position and # is the point where the wall indicates that it cannot pass through It's an empty grid. " A '-' f 'is the key and the corresponding lock is' a' - 'f'. To pass the lock, you must first get the corresponding key (case correspondence). Ask at least how many steps you can take to get all the keys.
Solution: there are many solutions, because there are few keys. BFS is the best. You can add a status to the ordinary BFS, indicating that you can get the key. You can further compress the state, but it's not necessary because the number is very small.
class Solution {
bool is_lock(char c){
return 'A' <= c && c <= 'F';
}
bool is_key(char c){
return 'a' <= c && c <= 'f';
}
struct state{
int r;
int c;
int k;
int step;
state(){};
state(int row, int col, int key, int s):r(row),c(col),k(key),step(s){}
};
int get_keys_num(vector<string>& grid){
int key_num = 0;
for(int i = 0;i < grid.size(); ++i)
for(int j = 0;j < grid[i].length(); ++j){
if(is_key(grid[i][j])) ++key_num;
}
return key_num;
}
pair<int,int> get_start(vector<string>& grid){
for(int i = 0;i < grid.size(); ++i)
for(int j = 0;j < grid[i].length(); ++j){
if(grid[i][j] == '@') return pair<int,int>(i, j);
}
return pair<int,int>(-1,-1);
}
public:
int shortestPathAllKeys(vector<string>& grid) {
int row = grid.size();
int col = grid[0].length();
int ans = INT_MAX;
bool vis[row][col][64];
queue<state> Q;
int key_num = get_keys_num(grid);
memset(vis, 0, sizeof(vis));
pair<int,int> start = get_start(grid);
Q.push(state(start.first, start.second, 0, 0));
int four_dir_r[] = {1, -1, 0, 0};
int four_dir_c[] = {0, 0, 1, -1};
while(!Q.empty()){
state cur = Q.front(); Q.pop();
if(__builtin_popcount(cur.k) == key_num) return cur.step;
int cur_r = cur.r;
int cur_c = cur.c;
int next_step = cur.step + 1;
int cur_k = cur.k;
if(vis[cur_r][cur_c][cur_k]) continue;
vis[cur_r][cur_c][cur_k] = true;
for(int i = 0;i < 4; ++i){
state next_state;
int next_r = cur_r + four_dir_r[i];
int next_c = cur_c + four_dir_c[i];
next_state.r = next_r;
next_state.c = next_c;
next_state.step = next_step;
next_state.k = cur_k;
if(next_r < 0 || next_c < 0 || next_r >= row || next_c >= col) continue;
if(grid[next_r][next_c] == '#') continue;
if(grid[next_r][next_c] == '.' || grid[next_r][next_c] == '@'){
Q.push(next_state);
}else if(is_key(grid[next_r][next_c])){
next_state.k = cur_k | (1 << (grid[next_r][next_c] - 'a'));
Q.push(next_state);
}else if(is_lock(grid[next_r][next_c])){
//return (grid[next_r][next_c] - 'A');
if(cur_k & (1 << (grid[next_r][next_c] - 'A')))
Q.push(next_state);
}
}
}
return -1;
}
};
871. Minimum Number of Refueling Stops
Meaning: start driving from position 0, go in one direction, and start with startFuel gasoline. During this period, there are some gas stations at some locations. Stations [i] [0] and stations [i] [1] respectively represent the location and fuel volume of the ith gas station. Cars can hold as much gasoline as they want. Ask at least how many times you can add oil to reach your destination. The destination is target.
Dynamic programming: add the destination to the back of the gas station. dp[i][j] refers to the maximum amount of oil remaining after J times of refueling at the i-th gas station. If it is less than 0, it means it is unreachable. The answer is the smallest J of DP [n] [J] > = 0. Without such a j, the answer is - 1
class Solution {
public:
int minRefuelStops(int target, int startFuel, vector<vector<int>>& stations) {
long long dp[502][502] = {0};
memset(dp, -1, sizeof(dp));
dp[0][0] = startFuel;
vector<int> v;
v.push_back(target); v.push_back(1);
stations.push_back(v);
for(int i = stations.size() - 1; i > 0; --i) stations[i][0] -= stations[i - 1][0];
for(int i = 1; i <= stations.size(); ++i){
//if(i < stations.size()) stations[i][0] -= stations[i - 1][0];
for(int j = 0;j <= i; ++j){
if(dp[i - 1][j] >= stations[i - 1][0])
dp[i][j] = dp[i - 1][j];
if(j > 0 && dp[i - 1][j - 1] >= stations[i - 1][0])
dp[i][j] = max(dp[i][j], stations[i - 1][1] + dp[i - 1][j - 1]);
dp[i][j] -= stations[i - 1][0];
}
}
for(int i = 0;i <= stations.size(); ++i)
if(dp[stations.size()][i] >= 0) return i;
return -1;
}
};878. Nth Magical Number
Given two positive integers a and b (< = 40000), a number is called a magic number if it can be divided by a or b. Given an n (< = 1e9), find the nth magic number.
Each lcm(a,b) is a circular section. In each lcm(a,b), the number of magic numbers is num1 = a /lcm(a,b) + b/lcm(a,b) - 1. We only need to calculate how many LCMS (a, b) n contains, and the number is n / num1. The remaining number n% num1 is in an lcm(a,b), which can be obtained by dichotomy
class Solution {
public:
const long long MOD = 1e9 + 7;
long long gcd(long long a, long long b){
if(!b) return a;
return gcd(b, a%b);
}
long long lcm(long long a, long long b){
return a / gcd(a,b) * b;
}
int nthMagicalNumber(int n, int a, int b) {
long long ab_lcm = lcm(a, b);
long long num_per_lcm = ab_lcm / a + ab_lcm / b - 1;
long long num_lcm = n / num_per_lcm;
long long num_rm = n % num_per_lcm;
//cout << ab_lcm<<num_lcm<<num_rm<<endl;
long long left = 0, right = ab_lcm - 1;
while(left <= right){
long long mid = (right - left) / 2 + left;
if(mid / a + mid / b < num_rm)
left = mid + 1;
else
right = mid - 1;
}
//cout << right <<endl;
return (num_lcm * (ab_lcm % MOD) + right + 1) % MOD;
}
};879. Profitable Schemes
Given a backpack, capacity G, and some items, the occupied space is group[i], and the value is profit[i]. What are the number of options to put some of these items into the backpack with a value of no less than P?
Solution: typical knapsack problem. Dynamic programming. dp[i][j] refers to the number of schemes whose capacity is used up and the profit is j, and dp[i][P] refers to the number of schemes whose profit is greater than or equal to P. Initialization dp[0][0] = 1. We first calculate the number of various value schemes of the first k items. Then, from these schemes, add the k+1 item to get the scheme number of various values of the first k+1 item.
class Solution {
public:
int profitableSchemes(int G, int P, vector<int>& group, vector<int>& profit) {
const long long MOD = 1e9 + 7;
//dp[i][j] refers to the number of schemes that use I individuals to make a profit of j dp[i][P] number of schemes with profit at least p
long long dp[101][102];
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for(int k = 0; k < group.size(); ++k){
for(int i = G - group[k]; i >= 0; --i){
for(int j = 0; j <= P; ++j){
if(!dp[i][j]) continue;
dp[i][j] %= MOD;
dp[i + group[k]][min(P, j + profit[k])] += dp[i][j];
}
}
}
long long ans = 0;
for(int i = 0;i <= G; ++i) ans += dp[i][P];
ans %= MOD;
return int(ans);
}
};
891. Sum of Subsequence Widths
Given an array with a length of 1 to 20000, each number is also 1 to 20000. For a subsequence, its width is the difference between the largest and smallest numbers in the subsequence. Ask the width and sum of all subsequences. Answer module 1e9+7
Solution: we only need to find out how many subsequences of each number A[i] take it as the minimum value and how many subsequences take it as the maximum value. Let's sort the array first. If an element A[i] is taken as the minimum value, the other elements must be behind it (all larger than him), so the sequence number of it as the minimum value is 2 ^ {the number larger than him}, that is, the sequence formed by taking or not taking each number.
class Solution {
public:
int sumSubseqWidths(vector<int>& A) {
sort(A.begin(), A.end());
const long long MOD = 1e9 + 7;
long long left = 0, right = 0;
vector<long long> two_pow(A.size() + 1,0);
two_pow[0] = 1;
for(int i = 1;i < two_pow.size(); ++i){
two_pow[i] = (two_pow[i - 1] << 1) % MOD;
}
for(int i = 0;i < A.size(); ++i){
left += A[i] * two_pow[A.size() - i - 1];
right += A[i] * two_pow[i];
left %= MOD;
right %= MOD;
}
return ((right - left) % MOD + MOD) % MOD;
}
};
895. Maximum Frequency Stack
Realize a data structure. Put data in the push. pop returns the number with the highest frequency. If there is one with the same frequency, output the last one.
Solution: using multiple stacks. Each stack stores the number of each frequency. Then use a map to store the frequency of the number.
class FreqStack {
stack<int> S[10001];
map<int, int> freq;
int max_freq;
public:
FreqStack() {
max_freq = 0;
}
void push(int x) {
int x_freq = ++freq[x];
S[x_freq].push(x);
max_freq = max(max_freq, x_freq);
}
int pop() {
int x = S[max_freq].top();
S[max_freq].pop();
if(S[max_freq].empty()) --max_freq;
--freq[x];
return x;
}
};
/**
* Your FreqStack object will be instantiated and called as such:
* FreqStack* obj = new FreqStack();
* obj->push(x);
* int param_2 = obj->pop();
*/903. Valid Permutations for DI Sequence
Question meaning: given a string S, the length is n, and contains two characters, D and I("decreasing" and "increasing"). A legal arrangement from 0 to n is that the relationship between the number a of position I and the number B of position i+1 is a > b (if S [i] = ='d '), a < B (if S [i] = = ='I'). Find the number of legal permutations
Solution: dynamic programming, dp[i][j] represents the arrangement of i+1 numbers from 0 to I, and the last number is the legal arrangement number of j (corresponding to the prefix I characters of S). The answer is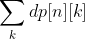
The last number is j, preceded by the remaining i numbers divided by J from 0 to i. We ask for their legal ranking. Note that for numbers greater than j, we subtract one to get the arrangement from 0 to i - 1, which corresponds to the arrangement from 0 to i minus J one by one, and its legitimacy is also consistent. Therefore, the legal arrangement of 0 to i can be obtained from the legal arrangement of 0 to i-1. So just enumerate the first character of J and construct the transfer equation
If s [i] = ='d '
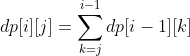
If S[i] == 'I'
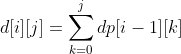
Every time we find dp[i][j], there is a summation operation. We can get it by summing the prefix in advance. In this way, the time complexity is O(n^2)
In addition, the use of space can be further reduced by scrolling the array
class Solution {
public:
int numPermsDISequence(string S) {
int n = S.length();
const long long MOD = 1e9 + 7;
vector<vector<long long> > dp(n + 1, vector<long long>(n + 1, 0));
dp[0][0] = 1;
for(int i = 1;i <= n; ++i){
for(int j = 0;j <= i ; ++j){
if(S[i - 1] == 'D'){
for(int k = j; k < i; ++k)
dp[i][j] += dp[i - 1][k];
}else{//S[i - 1] == 'I'
for(int k = 0; k < j; ++k)
dp[i][j] += dp[i - 1][k];
}
dp[i][j] %= MOD;
}
}
long long ans = 0;
for(int i = 0;i <= n; ++i) ans += dp[n][i];
return ans % MOD;
}
};
----------------------------------------
class Solution {
public:
int numPermsDISequence(string S) {
int n = S.length();
const long long MOD = 1e9 + 7;
vector<vector<long long> > dp(2, vector<long long>(n + 1, 0));
vector<vector<long long> > sum(2, vector<long long>(n + 2, 0));
dp[0][0] = 1;
sum[0][0] = 0;
sum[0][1] = 1;
for(int i = 1;i <= n; ++i){
for(int j = 0;j <= i ; ++j){
if(S[i - 1] == 'D'){
dp[i&1][j] = sum[1 - i&1][i] - sum[1 - i&1][j];
}else{//S[i - 1] == 'I'
dp[i&1][j] = sum[1 - i&1][j];
}
dp[i&1][j] %= MOD;
sum[i&1][j + 1] = dp[i&1][j] + sum[i&1][j];
}
}
return sum[n&1][n + 1] % MOD;
}
};906. Super Palindromes
Question meaning: give two numbers L,R (1 < = L,R < = 1e18 in the form of string). Ask how many numbers in the interval [L,R] are super palindromes.
Super palindrome refers to a number. First, it is a palindrome string. In addition, it is the square of a palindrome number.
If the super palindrome number is a^2, then a and a^2 are palindrome strings, a < = 1e9. We can enumerate half of a to get all palindromes.
Another solution is to print the table directly, because this condition is very harsh and the number satisfied will not be many. It is found that there are 71 with 0
Tabulation procedure
#include<bits/stdc++.h>
using namespace std;
bool is_palindrome(long long n){
long long m = 0;
long long tmp = n;
while(tmp){
m = m * 10 + tmp % 10 ;
tmp /= 10;
}
return m == n;
}
int main()
{
freopen("output.txt", "w", stdout);
vector<long long> a;
a.push_back(0);
a.push_back(1);
for(long long i = 2; i < 1e9; ++i){
if(i % 10 > 3 || i % 10 == 0) continue;
if(is_palindrome(i) && is_palindrome(i * i))
a.push_back(i * i);
}
cout<<'{';
for(int i = 0;i < a.size() - 1; ++i) cout<<a[i]<<',';
cout<<a[a.size() - 1]<<"};";
cout<<a.size()<<endl;
return 0;
}
-------------------------------------------—
class Solution {
public:
int superpalindromesInRange(string L, string R) {
long long super_palindrome[] ={0,1,4,9,121,484,10201,12321,14641,40804,44944,1002001,1234321,4008004,100020001,102030201,104060401,121242121,123454321,125686521,400080004,404090404,10000200001,10221412201,12102420121,12345654321,40000800004,1000002000001,1002003002001,1004006004001,1020304030201,1022325232201,1024348434201,1210024200121,1212225222121,1214428244121,1232346432321,1234567654321,4000008000004,4004009004004,100000020000001,100220141022001,102012040210201,102234363432201,121000242000121,121242363242121,123212464212321,123456787654321,400000080000004,10000000200000001,10002000300020001,10004000600040001,10020210401202001,10022212521222001,10024214841242001,10201020402010201,10203040504030201,10205060806050201,10221432623412201,10223454745432201,12100002420000121,12102202520220121,12104402820440121,12122232623222121,12124434743442121,12321024642012321,12323244744232321,12343456865434321,12345678987654321,40000000800000004,40004000900040004};
int len = 71;
long long l = stoll(L.c_str());
long long r = stoll(R.c_str());
return upper_bound(super_palindrome, super_palindrome + len ,r) - lower_bound(super_palindrome, super_palindrome + len, l);
}
};920 Number of Music Playlists
Given three numbers n, l, K < = 100. Fill the array with length L with numbers from 1 to N, each number appears at least once, and the continuous sub segments with length k cannot be repeated. Number of schemes for filling
Dynamic programming. Set the length of K [i] [DP] as the number of non contiguous sub segments of the array. The transfer equation is readily available, see code.
class Solution {
public:
static const int maxn = 101;
long long dp[maxn][maxn];
//long long C[maxn][maxn];
long long MOD = 1e9 + 7;
int numMusicPlaylists(int N, int L, int K) {
memset(dp, 0, sizeof(dp));
//dp[i][j] length I uses j characters. There are no duplicate schemes in each K
dp[0][0] = 1;
for(int i = 1;i <= L; ++i){
for(int j = 1; j <= min(i, N); ++j){
dp[i][j] = (dp[i - 1][j] * max(j - K, 0) + dp[i - 1][j - 1] * max(0, N - j + 1)) % MOD;
}
}
return dp[L][N];
}
};952. Largest Component Size by Common Factor
Given n numbers, it means n nodes. If two node values are not coprime, there is an edge between the nodes. How many points are there in the maximum connected component. You can find the prime factor for each number first. If two numbers have a common factor, the smallest one must be a prime factor. We treat each prime as a bucket and place a factor as its number. When there is a number with factor A and factor b, the numbers of the two buckets are merged (they are the same connected component). This process is completed with and query set.
class Solution {
// //Euler sieve
// vector<int> get_primer_euler(int maxn){
// vector<int> prime(maxn, 1);
// int prime_num = 0;
// for(size_t i = 2;i < maxn; ++i){
// if(prime[i])
// prime[prime_num++]=i;
// for(size_t j = 0;j < prime_num and prime[j] * i < maxn; ++j){
// prime[prime[j] * i] = false;
// If (I% prime [J] = = 0) / / ensure that each composite number will only be screened out by its minimum prime factor, so each number will only be marked once
// break;
// }
// }
// //cout<<prime_num<<endl;
// prime.resize(prime_num);
// return prime;
// }
int find_pa(int x, unordered_map<int, int> &pa){
if(pa.count(x) == 0) return pa[x] = x;
return x == pa[x]? x : pa[x] = find_pa(pa[x], pa);
}
public:
int largestComponentSize(vector<int>& A) {
//int n = 100001;
unordered_map<int,int> nums;
unordered_map<int, int> pa;
int ans = 1;
//Prime factor
for(int i = 0;i < A.size(); ++i){
if(A[i] == 1) continue;
int prev_fa = -1, cur_fa;
for(int j = 2;j <= sqrt(A[i]); ++j){
if(A[i] % j) continue;
while(A[i] % j == 0) A[i] /= j;
cur_fa = find_pa(j, pa);
if(prev_fa == -1) {
++nums[prev_fa = cur_fa];
continue;
}
if(cur_fa == prev_fa) continue;
pa[cur_fa] = prev_fa;
nums[prev_fa] += nums[cur_fa];
}
if(A[i] > 1) {
cur_fa = find_pa(A[i], pa);
if(prev_fa == -1) {
++nums[prev_fa = cur_fa];
}
if(cur_fa != prev_fa){
pa[cur_fa] = prev_fa;
nums[prev_fa] += nums[cur_fa];
}
}
ans = max(ans, nums[prev_fa]);
}
return ans;
}
};There are two others who don't know which one
After traversing the tree, give it a fork. Non recursive required
Solution: Morris traversal Post order traversal. The code is copied.
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
void reverseNodes(TreeNode* start, TreeNode* end) {
if (start == end) return;
TreeNode* x = start;
TreeNode* y = start -> right;
TreeNode* z;
while (x != end) {
z = y -> right;
y -> right = x;
x = y;
y = z;
}
}
void print(TreeNode* start, TreeNode* end, vector<int>& nodes) {
reverseNodes(start, end);
TreeNode* node = end;
while (true) {
nodes.push_back(node -> val);
if (node == start) break;
node = node -> right;
}
reverseNodes(end, start);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int> nodes;
TreeNode* dump = new TreeNode(0);
dump -> left = root;
TreeNode* cur = dump;
while (cur) {
if (cur -> left) {
TreeNode* pre = cur -> left;
while (pre -> right && pre -> right != cur)
pre = pre -> right;
if (!(pre -> right)) {
pre -> right = cur;
cur = cur -> left;
}else {
print(cur -> left, pre, nodes);
pre -> right = NULL;
cur = cur -> right;
}
}
else cur = cur -> right;
}
return nodes;
}
};
Like 24, it's just k Continuous node
Solution: almost
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* l1, *l2, *tmp = new ListNode(0), *p, *nextP;
tmp->next = head;
head = tmp;
while(tmp){
p = tmp->next;
bool flag = false;
for(int i = 0; i < k; ++i){
if(!p){flag = true;break;}
p = p->next;
}
if(flag) break;
l1 = tmp->next;
nextP = l1;
for(int i = 0;i < k; ++i){
l2 = l1->next;
l1->next = p;
p = l1;
l1 = l2;
}
tmp->next = p;
tmp = nextP;
}
tmp = head->next;
delete head;
return tmp;
}
};