Leetcode problem solving - Mathematics
204. Count prime
Count the number of all prime numbers less than non negative integer n. (the definition of prime is very simple. If a number can only be divided by 1 and itself, then the number is prime.)
Input: n = 10 Output: 4 Explanation: there are four prime numbers less than 10, They are two, 3, 5, 7 .
Solution idea: if enumeration method is adopted, the idea is as follows:
int countPrimes(int n) {
int count = 0;
for (int i = 2; i < n; i++)
if (isPrim(i)) count++;
return count;
}
// Judge whether integer n is prime
boolean isPrime(int n) {
for (int i = 2; i < n; i++)
if (n % i == 0)
// There are other divisible factors
return false;
return true;
}
In this way, the time complexity O(n^2) is a big problem.
Next, we introduce a common algorithm, which was proposed by the Greek mathematician eradosse, which is called eradosse sieve method, or Elsevier sieve for short.
First, i does not need to traverse to N, but only to sqrt(n). Why? Let's take an example and assume n = 12.
12 = 2 × 6 12 = 3 × 4 12 = sqrt(12) × sqrt(12) 12 = 4 × 3 12 = 6 × 2
As you can see, the last two products are the first two. Conversely, the dividing point of inversion is sqrt(n). In other words, if no divisible factor is found in the interval [2,sqrt(n)], it can be directly concluded that n is a prime number, because no divisible factor will be found in the interval [sqrt(n),n].
In addition, we consider the fact that if x is a prime number, then the multiple of x greater than x 2x,3x,... Must not be a prime number, so we can start here.
Let isPrime[i] indicate whether the number I is a prime number. Traverse each number from small to large. If the number is a prime number, mark all its multiples as false (except the prime number itself), so that we can know the number of prime numbers at the end of the run.
Of course, we can continue to optimize here. For a prime number x, if we mark it from 2x as mentioned above, it is actually redundant, because 2x,3x,... These numbers must be marked by multiples of other numbers before X. for example, when i = 4, the algorithm will mark 4 × 2 = 8,4 × 3 = 12 and so on, but 8 and 12 have been replaced by 2 of i = 2 and i = 3 × 4 and 3 × 4 marked. We can optimize it a little bit and let j traverse from the square of i
int countPrimes(int n) {
boolean[] isPrim = new boolean[n];
Arrays.fill(isPrim, true);
for (int i = 2; i * i < n; i++)
if (isPrim[i])
for (int j = i * i; j < n; j += i)
isPrim[j] = false;
int count = 0;
for (int i = 2; i < n; i++)
if (isPrim[i]) count++;
return count;
}
Maximum common divisor and minimum common multiple
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
The least common multiple is the product of two numbers divided by the greatest common divisor.
int lcm(int a, int b) {
return a * b / gcd(a, b);
}
Binary conversion
504. Hex number (simple)
Given an integer, convert it to 7-ARY and output it as a string.
input: 100 output: "202"
input: -7 output: "-10"
Note: the input range is [- 1e7, 1e7]. Pay extra attention to the handling of negative numbers!
class Solution {
public String convertToBase7(int num) {
if(num == 0) return "0";
StringBuilder sb = new StringBuilder();
//Flag bit to determine whether num is a negative number
boolean isNegative = num < 0;
if(isNegative) num = - num;
while(num > 0){
sb.append(num % 7);
num /= 7;
}
//Recall the process of binary conversion. Connect the remainder of division 7 upside down to get the converted number
String res = sb.reverse().toString();
return isNegative ? '-'+res : res;//Note here that if it is a negative number, add a minus sign in front of it
}
}
Static string toString (int num, int radius) in Java can convert an integer into a string represented by radix.
public String convertToBase7(int num) {
return Integer.toString(num, 7);
}
405. Converting numbers to hexadecimal numbers (simple)
Given an integer, write an algorithm to convert this number into hexadecimal number. For negative integers, we usually use Complement operation method.
be careful:
- All letters (a-f) in hexadecimal must be lowercase.
- Hexadecimal strings cannot contain extra leading zeros. If the number to be converted is 0, it is represented by a single character '0'; For other cases, the first character in the hexadecimal string will not be the 0 character.
- The given number is guaranteed to be in the range of 32-bit signed integers.
- You cannot use any method provided by the library to convert or format numbers directly to hexadecimal.
input:26 output:"1a"
input:-1 output:"ffffffff"
[note] the core idea is to use bit operation. Every four bits correspond to one hexadecimal digit.
- Use 0xf(00... 01111b) to obtain the lower 4 bits of num.
- Because the form of complement is considered, the sign bit cannot have special meaning. You need to use unsigned shift right > >, and fill in 0 on the left
- After all conversion, num == 0, so judge whether the final conversion is 0 or not
- Splice strings directly using StringBuilder
class Solution {
public String toHex(int num) {
char[] map = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f'};
if (num == 0) return "0";
StringBuilder sb = new StringBuilder();
//Move the highest bit to the right without sign and supplement 0. After all conversion, num == 0. Therefore, judge whether the conversion is completed by judging whether it is finally 0.
while(num != 0){
sb.append(map[num & 0xf]);
num >>>= 4;
}
return sb.reverse().toString();
}
}
168. Excel table column name - 26 base (simple)
Given a positive integer, return its corresponding column name in the Excel table.
1 -> A 2 -> B 3 -> C ... 26 -> Z 27 -> AA 28 -> AB ...
input: 28 output: "AB"
input: 701 output: "ZY"
Solution idea: the key to this problem lies in the processing of 0, because the 26 base range is [0, 25], but [A, Z] in the problem corresponds to [1, 26], so it is necessary to perform - 1 operation on n. In this way, we can convert n to hexadecimal, and then get each bit + 'A' and convert it into characters for string splicing, which is consistent with the idea of the first two questions.
class Solution {
public String convertToTitle(int columnNumber) {
if(columnNumber <= 0) return "";
StringBuilder sb = new StringBuilder();
while(columnNumber > 0){
columnNumber--;//This step is the key!!
sb.append((char)(columnNumber % 26 + 'A'));
columnNumber /= 26;
}
return sb.reverse().toString();
}
}
171. Excel table column serial number (simple)
Given the column name in an Excel table, return its corresponding column sequence number. (opposite to the previous question)
A -> 1 B -> 2 C -> 3 ... Z -> 26 AA -> 27 AB -> 28 ...
input: "AB" output: 28
class Solution {
public int titleToNumber(String columnTitle) {
int ans = 0;
char[] c = columnTitle.toCharArray();
for(int i = 0; i < c.length; i++){
//Note the plus one here
ans = ans*26 + (c[i] - 'A' + 1);
}
return ans;
}
}
Factorial
172. How many zeros are there in the tail of statistical factorial (simple)
Given an integer n, return n! The number of zeros in the mantissa of the result.
input: 3 output: 0 explain: 3! = 6, There is no zero in the mantissa.
input: 5 output: 1 explain: 5! = 120, 1 zero in mantissa.
First, the result of multiplying two numbers has 0 at the end. It must be because there are factors 2 and 5 in the two numbers, because 10 = 2 x 5. In other words, the problem turns into: n! How many factors 2 and 5 can be decomposed at most?
For example, n = 25, then 25! How many 2 and 5 can be decomposed at most? This mainly depends on how many factors 5 can be decomposed, because each even number can be decomposed into factor 2, which must be much more than factor 5.
25! 5 can provide one, 10 can provide one, 15 can provide one, 20 can provide one, 25 can provide two. There are 6 factors 5 in total, so 25! There are six zeros at the end of the result.
Now, the question turns into: n! How many factors 5 can be decomposed at most?
The difficulty is that numbers like 25 and 50125 can provide more than one factor 5. How can they not be missed?
In this way, let's assume n = 125 and calculate 125! There are several zeros at the end of the result:
First, 125 / 5 = 25. This step is to calculate how many multiples of 5, such as 5, 15, 20 and 25, they must provide a factor 5.
But are these enough? As I said just now, the multiples of 25, such as 25, 50 and 75, can provide two factors 5, so let's calculate 125! There are 125 / 25 = 5 multiples of 25, each of which can provide an additional factor of 5.
Is that enough? We found that 125 = 5 x 5 x 5. The multiples of 125, such as 125250, can provide three factors 5, so we have to calculate 125 again! There is 125 / 125 = a multiple of 125, which can also provide an additional factor of 5.
That should be enough, 125! Up to 25 + 5 + 1 = 31 factor 5 can be decomposed, that is, there are 31 zeros at the end of the factorial result.
Conclusion: * * for a number n, it contains 5 numbers: N/5 + N/5^2 + N/5^3 +..., * * where N/5 represents that the multiple of 5 in the number not greater than n contributes a 5, and N/5^2 represents that the multiple of 5 ^ 2 in the number not greater than n contributes another 5.
class Solution {
public int trailingZeroes(int n) {
int count = 0;
while(n > 0) {
count += n / 5;
n /= 5;
}
return count;
}
}
If the statistics is N! The position of the lowest 1 in the binary representation of as long as the number of 2 is counted. The number of 2 is N/2 + N/2^2 + N/2^3 +
793. K zeros after factorial function (difficult)
f(x) is x! At the end is the number of 0. (recall that X! = 1 * 2 * 3 *... * x, and 0! = 1)
For example, f(3) = 0, because 3= There is no 0 at the end of 6; And f(11) = 2, because 11= There are 2 zeros at the end of 39916800. Given K, find out how many nonnegative integers x can satisfy f(x) = K.
Input: K = 0 Output: 5 Explanation: 0!, 1!, 2!, 3!, and 4! All accord with K = 0 Conditions.
Input: K = 5 Output: 0 Explanation: there is no such match x!,accord with K = 5 Conditions.
An intuitive solution to violence is exhaustive, because with the increase of X, X! It must be incremental, trailingZeroes(x!) The pseudo code logic is as follows:
int res = 0;
for (int x = 0; x < +inf; x++) {
if (trailingZeroes(x) < K) {
continue;
}
if (trailingZeroes(x) > K) {
break;
}
if (trailingZeroes(x) == K) {
res++;
}
}
return res;
As the binary search algorithm mentioned earlier, for this monotonous function, you can use binary search to reduce the dimension by traversing the for loop. In fact, you are asking how many x satisfy trailingZeroes(x) == K. as soon as you subtract the maximum and minimum values, you can calculate how many x satisfy the conditions.
I analyzed the last question, X! How many zeros there are at the end depends on X! How many factors can be decomposed at most 5. Obviously, every time x + 5, the factorial will be multiplied by at least one more 5, and there will be at least one more 0 at the end, so if the above X has a solution, it is 5, and if there is no solution, it is 0
The key point is to determine the upper and lower bounds of the binary search interval. We can take 0 as the lower bound of X; For the upper bound, because x will have at least one more 0 at the end every + 5, when there are K zeros at the end, X is at most 5*K, so the upper boundary can take 5*K+1.
Note that to avoid integer overflow, all data types need to be changed to long:
class Solution {
public int preimageSizeFZF(long k) {//Note that the k here is changed to long
long left = 0, right = 5 * k + 1;
while(left < right){
long mid = left + (right - left)/2;
if(count(mid) < k){
left = mid + 1;
}else if(count(mid) > k){
right = mid;
}else{
return 5;//If k has a solution, it must be equal to 5;
}
}
return 0;//No solution is 0
}
//Solve n! Number of last 0
private int count(long n){
int sum = 0;
while(n > 0){
sum += n / 5;
n /= 5;
}
return sum;
}
}
String addition and subtraction
67. Binary summation (simple)
Give you two binary strings and return their sum (expressed in binary). The input is a non empty string and contains only the numbers 1 and 0
input: a = "11", b = "1" output: "100"
input: a = "1010", b = "1011" output: "10101"
Problem solving ideas: first adopt the simplest ideas to realize:
class Solution {
public String addBinary(String a, String b) {
int i = a.length() - 1, j = b.length() - 1;
StringBuilder sb = new StringBuilder();
int carry = 0;
while(i >= 0 && j >= 0){
int sum = a.charAt(i) - '0' + b.charAt(j) - '0';
sb.append((carry + sum) % 2);
carry = (sum + carry) / 2;
i--;
j--;
}
while(i >= 0){
int ai = a.charAt(i) - '0';
sb.append((ai + carry) % 2);
carry = (ai + carry) / 2;
i--;
}
while(j >= 0){
int bi = b.charAt(j) - '0';
sb.append((bi + carry) % 2);
carry = (bi+ carry) / 2;
j--;
}
if(carry == 1) sb.append(1);
return sb.reverse().toString();
}
}
Simplified version:
class Solution {
public String addBinary(String a, String b) {
StringBuilder ans = new StringBuilder(); //answer
int i = a.length() - 1, j = b.length() - 1; //Traverse from the end (bits)
int carry = 0; //carry
while(i >= 0 || j >= 0 || carry != 0) { //If two numbers are not traversed, or there is carry
if(i >= 0) carry += a.charAt(i--) - '0'; //If a has a number
if(j >= 0) carry += b.charAt(j--) - '0'; //If b still has a number
ans.append(carry % 2); //Add the sum of the current bit and take the module
carry /= 2; //carry
}
return ans.reverse().toString(); //Since the first bit is after the calculation, it should be reversed
}
}
415. String addition (simple)
Given two non negative integers num1 and num2 in string form, calculate their sum.
Solution idea: the idea is the same as that of the previous question, but this question is decimal addition. Just change the division and remainder operation of 2 to 10!
class Solution {
public String addStrings(String num1, String num2) {
int i = num1.length() - 1, j = num2.length() - 1;
StringBuilder sb = new StringBuilder();
int carry = 0;
while(carry != 0 || i >= 0 || j >= 0){
if(i >= 0) carry += num1.charAt(i--) - '0';
if(j >= 0) carry += num2.charAt(j--) - '0';
sb.append(carry % 10);
carry /= 10;
}
return sb.reverse().toString();
}
}
43. String multiplication (medium)
Given two nonnegative integers num1 and num2 in string form, return the product of num1 and num2, and their product is also expressed in string form.
input: num1 = "2", num2 = "3" output: "6"
input: num1 = "123", num2 = "456" output: "56088"
If one of num1 and num2 is 0, you can directly return 0 as the result.
If num1 and num2 are not 0, the product can be calculated by simulating "vertical multiplication". Traverse the multiplier from right to left, multiply each bit of the multiplier by the multiplied number to obtain the corresponding result, and then accumulate the results obtained each time. In this problem, the multiplicand is num1 and the multiplier is num2.
It should be noted that except for the lowest bit of num2, the operation result of each other bit needs to be supplemented with 0.
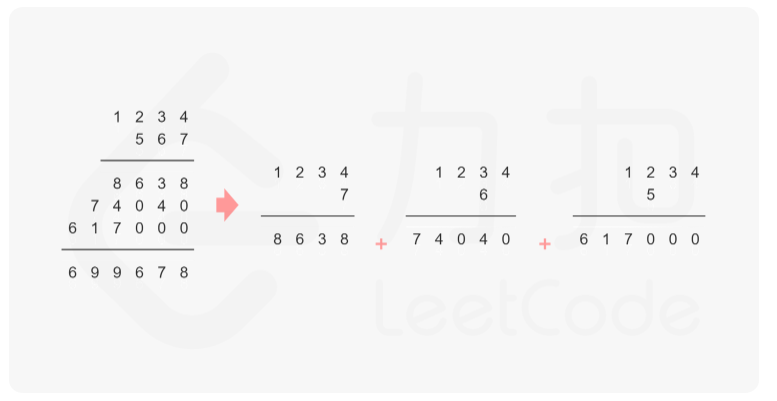
To accumulate the results obtained each time, you can use 415. String addition "Approach.
class Solution {
public String multiply(String num1, String num2) {
if(num1.equals("0") || num2.equals("0")){
return "0";
}
String ans = "";
// num2 multiplies num1 bit by bit
for(int i = num2.length() - 1; i >= 0; i--){
// Save the result of multiplying the i-th digit of num2 by num1
StringBuilder subSum = new StringBuilder();
// First, according to the corresponding position of i, fill 0 of the corresponding number in the result
for (int k = num2.length() - 1; k > i; k--) {
subSum.append(0);
}
// The process of multiplying the i-th digit of num2 by num1
int carry = 0;
for(int j = num1.length() - 1; j >= 0 || carry != 0; j--){
int a = j >= 0 ? num1.charAt(j) - '0' : 0;
int b = num2.charAt(i) - '0';
subSum.append((a * b + carry) % 10);
carry = (a * b + carry)/10;
}
// Sum the current result with the newly calculated result as the new result
ans = addStrings(ans, subSum.reverse().toString());
}
return ans;
}
// Add two string numbers and return the sum in string form
public String addStrings(String num1, String num2) {
int i = num1.length() - 1, j = num2.length() - 1;
StringBuilder sb = new StringBuilder();
int carry = 0;
while(carry != 0 || i >= 0 || j >= 0){
if(i >= 0) carry += num1.charAt(i--) - '0';
if(j >= 0) carry += num2.charAt(j--) - '0';
sb.append(carry % 10);
carry /= 10;
}
return sb.reverse().toString();
}
}
Encounter problem
453. Minimum number of moves to make array elements equal (simple)
Given a non empty integer array of length N, each operation will increase n - 1 elements by 1. Find the minimum number of operations to make all elements of the array equal.
Input:[1,2,3] Output: 3 Explanation: only 3 operations are required (note that each operation will increase the value of two elements): [1,2,3] => [2,3,3] => [3,4,3] => [4,4,4]
Solution idea: each operation mentioned in the title will increase n - 1 elements by 1. It can be imagined that this is actually reducing one element at a time. Then, in order to make each element equal, it must be reduced to the value of the smallest element in the end. Therefore, we only need to calculate the number of times each element is reduced to the value of the smallest element, and then sum it up is the final answer
public int minMoves(int[] nums) {
int min = nums[0];
for(int num : nums){
if(num < min){
min = num;
}
}
int move = 0;
for(int num : nums){
move += num - min;
}
return move;
}
462. Minimum number of moves to make array elements equal II (medium)
Given a non empty integer array, find the minimum number of moves required to make all array elements equal, where each move can add or subtract 1 from the selected element. You can assume that the length of the array is up to 10000.
input:[1,2,3] output:2 Note: only two actions are necessary (remember that only one element can be increased or decreased by 1 in each step): [1,2,3] => [2,2,3] => [2,2,2]
Solution: This is a classic mathematical problem. When x is the median of N numbers, the distance can be minimized. Specifically, if n is an odd number, X must be the unique median of the N numbers; If n is an even number, the middle two numbers are p and Q, and the median is (p + q) / 2, then x can be any number in the interval [p, q].
Therefore, we only need to find the median of this N number and calculate the sum of distances. We can sort the array directly, so we can get the median directly.
class Solution {
public int minMoves2(int[] nums) {
Arrays.sort(nums);
int mid = nums.length/2;
int move = 0;
for(int num : nums){
move += Math.abs(num - nums[mid]);
}
return move;
}
}
Majority voting question
169. Most elements (simple)
Given an array of size n, find most of its elements. Most elements refer to elements that appear more than ⌊ n/2 ⌋ in the array.
You can assume that the array is non empty and that there are always many elements in a given array.
Input:[3,2,3] Output: 3
Input:[2,2,1,1,1,2,2] Output: 2
Problem solving ideas:
Method 1: hash table: traverse the entire array and use HashMap to store each element and the number of occurrences. (where key is the value and value is the number of occurrences); Then traverse each Entry in the HashMap to find the value > num The key of length / 2 is enough.
class Solution {
public int majorityElement(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
for(int num : nums){
map.put(num, map.getOrDefault(num, 0) + 1);
if(map.get(num) > nums.length/2){
return num;
}
}
return -1;
}
}
Method 2: sorting: since there are elements with occurrences > ⌊ n/2 ⌋ in the array, the same elements are always adjacent in the array after sorting. That is, there is a long string of continuous subarrays composed of the same elements with a len gt h of > ⌊ n/2 ⌋. Then the element with subscript n/2 (subscript starts from 0) must be mode. Time complexity: O(nlog*n)*
class Solution {
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length / 2];
}
}
The following figure explains why this strategy is effective. In the following figure, the first example is the case where n is an odd number, and the second example is the case where n is an even number.
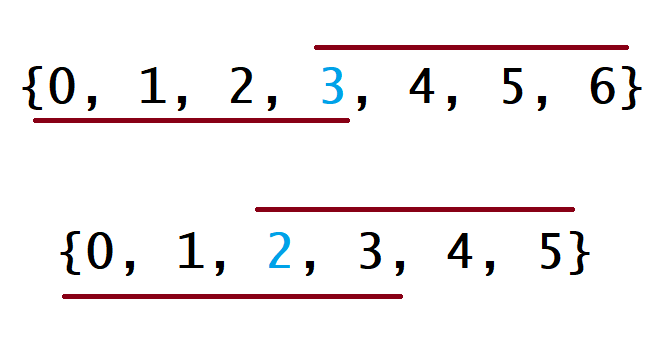
Method 3: Boyer Moore voting algorithm
The essence of Boyer Moore algorithm is very similar to divide and conquer. We first give the detailed steps of Boyer Moore algorithm:
We maintain a candidate mode candidate and its number of occurrences count. Initially, candidate can be any value, such as num [0], and count is 0;
We traverse all elements in the array nums. For each element x, before judging x, if the value of count is 0, we first assign the value of X to candidate (change candidate), and then we judge X:
-
If x is equal to candidate, the value of counter count increases by 1;
-
If x is not equal to candidate, the value of counter count decreases by 1.
After traversal, candidate is the mode of the whole array.
Why does this work?
The voting method is to encounter the same number of votes + 1, and encounter different numbers of votes - 1. And the number of "most elements" is > ⌊ n/2 ⌋, and the sum of the number of other elements is < = ⌊ n/2 ⌋. Therefore, the resu lt of the sum of the number of "most elements" - the number of other elements must be > = 1. This is equivalent to each "majority element" and other elements offsetting each other, and at least one "majority element" must remain in the end.
class Solution {
public int majorityElement(int[] nums) {
int candidate = nums[0], count = 0;
for(int num : nums){
if(count == 0) candidate = num;//If count is 0, replace the candidate
if(num == candidate){
count++;
}else{
count--;
}
}
return candidate;
}
}
229. Find mode ll (medium)
Given an integer array of size n, find out all elements that appear more than ⌊ n/3 ⌋ times.
**Advanced: * * try to design an algorithm with time complexity O(n) and space complexity O(1) to solve this problem.
Input:[3,2,3] Output:[3]
Input:[1,1,1,3,3,2,2,2] Output:[1,2]
Solution idea: the voting algorithm of question 169 is similar to that of question 169, but question 169 is to find a mode. As long as there is only one candidate, it is guaranteed that there must be a mode. Just vote directly, but this question does not guarantee that there must be more than n/3 of an element.
First of all, we have to make it clear that the maximum number of n/k modes is only k-1. Why? Suppose there are k modes, n/k * k=n, these k elements are modes, and they have to be different. How is it possible. So for this question, there can only be 3-1 = 2 more than n/3. We can choose two candidates a and B first. There are three ways to traverse the array:
- Candidate 1: > n / 3
- Candidate 2: > n / 3
- Others: < n / 3
Three steps to write code
1. If you vote for A (the current element is equal to A), the number of votes of A is + +;
2. If you vote for B (the current element is equal to b), the number of votes of B is + +;
3. If A and B do not vote (that is, they are not equal to A and B at present), check whether the number of votes of A or B is 0 at this time. If it is 0, the current element becomes A new candidate; If the votes of both candidates A and B are not zero, the votes of both candidates A and B will be reduced by one.
Finally, there are several possibilities: 2 are greater than n/3, 1 is greater than n/3, and 0 is greater than n/3. After the traversal, two candidates are selected, but whether the two candidates meet > n/3 needs to traverse the array again to find out the specific number of votes of the two candidates, because the question is not like question 169, which is guaranteed.
class Solution {
public List<Integer> majorityElement(int[] nums) {
List<Integer> res = new ArrayList<>();
if (nums == null || nums.length == 0) {
return res;
}
// Define two candidates and their votes
int cand1 = 0,cand2 = 0;
int cnt1 = 0, cnt2 = 0;
// Voting process
for (int num : nums) {
// In case of candidate 1, the number of votes++
if (num == cand1) {
cnt1++;
// Traverse again. If you don't want to write continue, you can write multiple else if
continue;
}
// In case of candidate 2, the number of votes++
if (num == cand2) {
cnt2++;
continue;
}
// It is neither cand1 nor cand2. If cnt1 is 0, it will do cand1
if (cnt1 == 0) {
cand1 = num;
cnt1++;
continue;
}
// If the number of cand1 is not 0 but the number of cand2 is 0, he will do cand2
if (cnt2 == 0) {
cand2 = num;
cnt2++;
continue;
}
// If the number of cand1 and cand2 is not 0, then both are - 1
cnt1--;
cnt2--;
}
// Check whether the two votes match
cnt1 = cnt2 = 0;
for (int num : nums) {
if (num == cand1) {
cnt1++;
} else if (num == cand2) {
// You must use else if here
// Because the use case of [0,0,0] may appear, the two cand s are the same, and the result of writing two if becomes [0,0]
cnt2++;
}
}
if (cnt1 > nums.length / 3) res.add(cand1);
if (cnt2 > nums.length / 3) res.add(cand2);
return res;
}
}
other
367. Effective complete square (simple)
Given a positive integer num, write a function. If num is a complete square number, it returns true, otherwise it returns false.
Advanced: do not use any built-in library functions, such as sqrt.
Problem solving ideas:
Method 1: binary search
class Solution {
public boolean isPerfectSquare(int num) {
int left = 1, right = num;
while(left <= right){
int mid = left + (right - left)/2;
int target = num / mid; //The time complexity of searching by target is much less than that of comparing directly by square
if(mid < target){
left = mid + 1;
}else if(mid > target){
right = mid -1;
}else{
//Pay attention here! When mid = num / mid and num% mid = = 0, mid is the square root
if(num % mid == 0) return true;
left = mid + 1;
}
}
return false;
}
}
Method 2: arithmetic sequence
Square sequence: 1,4,9,16,... Interval: 3,5,7
The interval is an equal difference sequence. Using this feature, you can get the square sequence starting from 1.
class Solution {
public boolean isPerfectSquare(int num) {
int subNum = 1;
while (num > 0) {
num -= subNum;
subNum += 2;
}
return num == 0;
}
}
326. Power of 3 (simple)
Given an integer, write a function to determine whether it is a power of 3. If yes, return true; Otherwise, false is returned.
The integer n is to the power of 3, which needs to be satisfied: there is an integer x so that n == 3x
Input: n = 27 Output: true
Input: n = 0 Output: false
class Solution {
public boolean isPowerOfThree(int n) {
if (n < 1) {
return false;
}
while (n % 3 == 0) {
n /= 3;
}
return n == 1;
}
}
628. Maximum product of three numbers (simple)
Give you an integer array nums, find the maximum product of three numbers in the array, and output this product.
Input: nums = [1,2,3] Output: 6
Input: nums = [-1,-2,-3] Output:-6
Problem solving ideas:
In fact, all positive numbers and all negative numbers are the same. They are the product of the largest three. Because the results of the three negative numbers must be negative, the negative number with small absolute value is required, so the maximum three negative numbers are still taken.
The second situation is positive and negative. If most of them are positive numbers and there is only one negative number, it is still the multiplication of the three largest numbers; If there is more than one negative number, it may be that after multiplying the two smallest negative numbers, the negative will be positive, get a large number, and then multiply it by the largest positive number. It may also be that the absolute value of negative numbers is very small, while the absolute value of positive numbers is very large. At this time, it is still the multiplication of the three largest numbers.
To sum up, there are only two results in total, the largest three numbers are multiplied, or the two minimum and maximum values are multiplied.
Method 1: sorting
class Solution {
public int maximumProduct(int[] nums) {
Arrays.sort(nums);
int n = nums.length;
return Math.max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);
}
}
In fact, we only require the maximum three numbers and the minimum two numbers in the array, so we can directly obtain these five numbers by linear scanning without sorting.
class Solution {
public int maximumProduct(int[] nums) {
int max1 = Integer.MIN_VALUE, max2 = Integer.MIN_VALUE, max3 = Integer.MIN_VALUE;
int min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE;
for(int num : nums){
if(num > max1){
max3 = max2;
max2 = max1;
max1 = num;
}else if(num > max2){
max3 = max2;
max2 = num;
}else if(num > max3){
max3 = num;
}
if(num < min1){
min2 = min1;
min1 = num;
}else if(num < min2){
min2 = num;
}
}
return Math.max(max1*max2*max3, min1*min2*max1);
}
}
238. Product of arrays other than itself (medium)
Give you an integer array nums with length N, where n > 1, and return the output array output, where output[i] is equal to the product of other elements in nums except nums[i].
input: [1,2,3,4] output: [24,12,8,6]
Note: Please * * do not use division, * * and complete the problem within O(n) time complexity.
Solution idea: we do not have to divide the product of all numbers by the number at a given index to get the corresponding answer, but use the product of all numbers on the left of the index and the product of all numbers on the right (i.e. prefix and suffix) to get the answer.
For a given index i, we will multiply the product of all the numbers on its left by the product of all the numbers on its right. Let's describe this algorithm in more detail.
Algorithm:
- Initialize two empty arrays L and r. For a given index I, L[i] represents the product of all numbers to the left of I, and R[i] represents the product of all numbers to the right of I.
- We need two loops to fill in the values of the L and R arrays. For array L, L[0] should be 1 because there is no element to the left of the first element. For other elements: L[i] = L[i-1] * nums[i-1].
- Similarly, for array R, R[length-1] should be 1. Length refers to the size of the input array. Other elements: R[i] = R[i+1] * nums[i+1].
- When the R and L arrays are filled, we only need to iterate on the input array, and the value at index I is: L[i] * R[i].
class Solution {
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
// L and R represent the product list on the left and right sides respectively
int[] L = new int[length];
int[] R = new int[length];
int[] answer = new int[length];
// L[i] is the product of all elements to the left of index I
// For the element with index '0', L[0] = 1 because there is no element on the left
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] is the product of all elements to the right of index I
// For the element with index 'length-1', because there is no element on the right, R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// For index I, the product of all elements except num [i] is the product of all elements on the left multiplied by all elements on the right
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
}