Time: 22:30-24:00, February 5, 2022
Address: Competition - leetcode
Outcome:
5984. Minimum sum of the last four digits after splitting
Difficulty: simple
I'll give you a four digit , positive integer , num. Please use the , digit in , num , and split , num , into two new integers , new1 , and , new2. New1 , and , new2 , can have , leading 0, and all , digits in , num , must be used.
- For example, if you give , num = 2932, the digits you have include: two , 2, one , 9 , and one , 3. Some possible [new1, new2] number pairs are [22, 93], [23, 92], [223, 9] and [2, 329].
Please return the , minimum , sum of , new1 , and , new2 , you can get.
Example 1:
Input: num = 2932 Output: 52 Explanation: the feasible [new1, new2] number pairs are [29, 23], [223, 9] and so on. The minimum sum is the sum of number pairs [29, 23]: 29 + 23 = 52.
Example 2:
Input: num = 4009 Output: 13 Explanation: the feasible [new1, new2] number pairs are [0, 49], [490, 0], etc. The minimum sum is the sum of number pairs [4, 9]: 4 + 9 = 13.
Tips:
- 1000 <= num <= 9999
Idea: the idea obtained from the topic is very intuitive. Considering the various restrictions in the topic and the value range of num, there is no special situation to deal with. After simple sorting, put the smallest two numbers in ten places and the rest in one place. You can get and.
Competition answer:
class Solution {
public int minimumSum(int num) {
List<Integer> list = new ArrayList<>();
while (num > 0) {
list.add(num % 10);
num = num / 10;
}
Collections.sort(list);
return 10 * list.get(0) + 10 * list.get(1) + list.get(2) + list.get(3);
}
}Follow up: in fact, some experts take the value of each digit of num through String, which can avoid making mistakes in the loop, but the whole idea remains the same.
class Solution {
public int minimumSum(int num) {
String s = String.valueOf(num);
List<Integer> list = new ArrayList<>();
for (int i = 0; i < s.length(); i++) {
list.add(s.charAt(i) - '0');
}
Collections.sort(list);
return 10 * list.get(0) + 10 * list.get(1) + list.get(2) + list.get(3);
}
}5985. Divide the array according to the given number
Difficulty: medium
Give you an array of integers with subscripts starting from , 0 , num , and an integer , pivot. Please rearrange {num} so that the following conditions are true:
- All elements less than # pivot # appear before all elements greater than # pivot #.
- All elements equal to , pivot , appear between elements less than and greater than , pivot ,.
- The relative order of elements between pivot and pivot is not less than.
- More formally, consider each pair of pi, pj, pi , is the new position of the initial position , I , element, and pj , is the new position of the initial position , j , element. For elements less than "pivot", if "I < j" and "num [i] < pivot" and "num [j] < pivot" are true, then "pi < pj" is also true. Similarly, for elements greater than , pivot , if , I < j and , num [i] > pivot , and , num [j] > pivot , are true, then , pi < pj.
Please return the result array after rearranging the {num} array.
Example 1:
Input: num = [9,12,5,10,14,3,10], pivot = 10 Output: [9,5,3,10,10,12,14] Explanation: Elements 9, 5 and 3 are smaller than pivot, so they are at the far left of the array. Elements 12 and 14 are larger than pivot, so they are at the far right of the array. The relative positions of elements smaller than pivot and elements larger than pivot are [9, 5, 3] and [12, 14] respectively, and their relative order in the result array needs to be preserved.
Example 2:
Input: num = [- 3,4,3,2], pivot = 2 Output: [- 3,2,4,3] Explanation: Element - 3 is smaller than pivot, so it is on the far left of the array. Elements 4 and 3 are larger than pivot, so they are at the far right of the array. The relative positions of elements smaller than pivot and elements larger than pivot are [- 3] and [4,3] respectively, and their relative order in the result array needs to be preserved.
Tips:
- 1 <= nums.length <= 105
- -106 <= nums[i] <= 106
- pivot , is equal to an element in , num ,.
Idea: at first, I thought it was a quick index, and then I could sort the values on both sides, but after careful thinking, it was not so simple, because it could not guarantee the relative order between the numbers. If you use double pointers, it is also difficult to reasonably place the position of each value. Considering that it should be completed within the time complexity of O(n), I hurriedly thought of traversing the count first, counting the numbers equal to and less than pivot in advance, recycling once, and placing the numbers greater than or equal to and less than pivot respectively.
Competition answer:
class Solution {
public int[] pivotArray(int[] nums, int pivot) {
int count1 = 0;
int count2 = 0;
for (int i : nums) {
if (i < pivot) {
count1++;
}
if (i == pivot) {
count2++;
}
}
int[] res = new int[nums.length];
int t1 = 0;
int t2 = count1;
int t3 = count1 + count2;
for (int i = 0; i < nums.length; i++) {
if (nums[i] < pivot) {
res[t1++] = nums[i];
} else if (nums[i] == pivot) {
res[t2++] = nums[i];
} else if (nums[i] > pivot) {
res[t3++] = nums[i];
}
}
return res;
}
}
Follow up: in fact, most of the ideas are the same, but the code can be simplified a lot. One idea is to cycle, store numbers greater than or equal to or less than pivot through three list s, and then convert them into results. Of course arignote The strength of the big man is in the process of learning.
class Solution {
public int[] pivotArray(int[] nums, int pivot) {
return Arrays.stream(nums).boxed()
.sorted((o, p) -> Integer.compare(Integer.compare(o, pivot),
Integer.compare(p, pivot))).mapToInt(i -> i).toArray();
}
}5986. Minimum cost of setting time
Difficulty: medium
Common microwave ovens can set heating time, and the heating time meets the following conditions:
- At least 1} second.
- Up to 99 minutes and 99 seconds.
You can set the heating time by {entering up to} 4 numbers}. If the number of digits you enter is less than 4, the microwave oven will automatically prefix , 0 , to make up for 4 digits. The microwave oven will take the first two digits of the set four digits as minutes and the last two digits as seconds. The total time they represent is the heating time. For example:
- You enter , 9 , 5 , 4 (three numbers), which is automatically supplemented as , 0954 and represents , 9 , minutes , 54 , seconds.
- You enter 0 , 0 , 0 , 8 (four numbers), which means , 0 , 0 , 8 , 0 minutes , 8 , seconds.
- If you enter # 8 # 0 # 9 # 0, it means # 80 # minutes # 90 # seconds.
- If you enter # 8 # 1 # 3 # 0, it means # 81 # minutes # 30 # seconds.
Here are the integers , startAt, moveCost, pushCost , and , targetSeconds. At first, your finger is at the number "startAt". Moving your finger to # any other number costs # moveCost # per unit. Each time you enter the number where your finger is located, it costs a unit price of # pushCost #.
There may be many ways to set the heating time of , targetSeconds , seconds. You want to know the minimum total cost of these methods.
Please return to the minimum cost of setting the heating time of {targetSeconds} seconds.
Remember, although the seconds of the microwave oven can be set to 99 , seconds at most, one minute is equal to 60 , seconds.
Example 1:
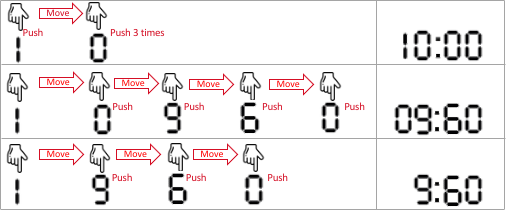
Input: startAt = 1, moveCost = 2, pushCost = 1, targetSeconds = 600 Output: 6 Explanation: here are all the ways to set the heating time. -10 minutes, 0 seconds, 0 seconds. At the beginning, the finger is at the number 1, enter 1 (cost 1), move to 0 (cost 2), enter 0 (cost 1), enter 0 (cost 1), and enter 0 (cost 1). The total cost is: 1 + 2 + 1 + 1 + 1 = 6. This is the lowest cost of all schemes. -0 9 6 0 means 9 minutes 60 seconds. It also means 600 seconds. Move the finger to 0 (cost 2), enter 0 (cost 1), move to 9 (cost 2), enter 9 (cost 1), move to 6 (cost 2), enter 6 (cost 1), move to 0 (cost 2), and enter 0 (cost 1). The total cost is: 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 + 2 + 1 = 12. -9 6 0, the automatic completion of microwave oven is 0960, which means 9 minutes and 60 seconds. Move the finger to 9 (cost 2), enter 9 (cost 1), move to 6 (cost 2), enter 6 (cost 1), move to 0 (cost 2), enter 0 (cost 1). The total cost is: 2 + 1 + 2 + 1 + 2 + 1 = 9.
Example 2:

Input: startAt = 0, moveCost = 1, pushCost = 2, targetSeconds = 76 Output: 6 Explanation: the best solution is to input two numbers 7 and 6, which means 76 seconds. Move the finger to 7 (cost 1), enter 7 (cost 2), move to 6 (cost 1), enter 6 (cost 2). The total cost is: 1 + 2 + 1 + 2 = 6 Other feasible schemes are 0076076016 and 116, but their costs are greater than 6.
Tips:
- 0 <= startAt <= 9
- 1 <= moveCost, pushCost <= 105
- 1 <= targetSeconds <= 6039
Idea: this question is really a bit of a mindset. It took two or three minutes to read the question alone. After reading it, it is easy to know that this is not an algorithm, but a solution to practical problems. Carefully analyze the time and realize that there are actually only two representations for any number of seconds entered (0960 in easy to get example 1 must not be better than 960). And there are only two kinds of seconds within 40. For example, 9 minutes and 30 seconds can be expressed as 8 minutes and 90 seconds, but 9 minutes and 40 seconds can not be expressed as 8 minutes and 100 seconds. In particular, even 9 minutes and 0 seconds can not be expressed as 7 minutes and 120 seconds, which can be quickly obtained. In order to avoid being interfered by some special situations, special treatment shall be made for situations within 60 seconds and 99 minutes - 5940 seconds.
Answer to the competition: (in fact, the condition greater than 5940 is problematic, but if the case is passed, it should be greater than 5979)
class Solution {
public int minCostSetTime(int startAt, int moveCost, int pushCost, int targetSeconds) {
if (targetSeconds < 60) {
return getCost(0, targetSeconds, startAt, moveCost, pushCost);
} else if (targetSeconds > 5940) {
return getCost(99, targetSeconds - 99 * 60, startAt, moveCost, pushCost);
}
int seconds = targetSeconds % 60;
int minutes = targetSeconds / 60;
if (seconds >= 40) {
return getCost(minutes, seconds, startAt, moveCost, pushCost);
} else {
return Math.min(getCost(minutes, seconds, startAt, moveCost, pushCost), getCost(minutes - 1, seconds + 60, startAt, moveCost, pushCost));
}
}
private int getCost(int minutes, int targetSeconds, int startAt, int moveCost, int pushCost) {
int num = minutes * 100 + targetSeconds;
List<Integer> list = new ArrayList<>();
while (num > 0) {
list.add(num % 10);
num = num / 10;
}
Collections.reverse(list);
int res = 0;
if (list.get(0) == startAt) {
res += pushCost;
} else {
res += (moveCost + pushCost);
}
for (int i = 1; i < list.size(); i++) {
if (list.get(i) == list.get(i - 1)) {
res += pushCost;
} else {
res += (moveCost + pushCost);
}
}
return res;
}
}
Follow up: it doesn't involve algorithms. Everyone's ideas are basically the same. The writing method can be simplified, so we don't make records.
5987. Minimum difference between and after deleting elements
Difficulty: difficulty
I'll give you an array of integers with subscripts starting from # 0 # num, which contains # 3 * n # elements.
You can delete exactly # n # elements from # num # and the remaining # 2 * n # elements will be divided into two # parts of the same size.
- The first n elements belong to the first part, and their sum is recorded as # sumfirst.
- The following n elements belong to the second part, and their sum is recorded as # sumsecond.
The difference , between the sum of the two parts is recorded as , sumfirst - sumsecond.
- For example, if sumfirst = 3 , and sumsecond = 2, their difference is , 1.
- For another example, if sumfirst = 2 , and sumsecond = 3, their difference is - 1.
Please return to the minimum value of the difference between the sum of the remaining two parts after deleting n elements.
Example 1:
Input: num = [3,1,2] Output: - 1 Explanation: nums has three elements, so n = 1. So we need to delete one element from nums and divide the remaining elements into two parts. -If we delete num [0] = 3, the array becomes [1,2]. The difference between the sum of the two parts is 1 - 2 = - 1. -If we delete num [1] = 1, the array becomes [3,2]. The difference between the sum of the two parts is 3 - 2 = 1. -If we delete num [2] = 2, the array becomes [3,1]. The difference between the sum of the two parts is 3 - 1 = 2. The minimum difference between the sum of two parts is min(-1,1,2) = -1.
Example 2:
Input: num = [7,9,5,8,1,3] Output: 1 Explanation: n = 2. So we need to delete two elements and divide the remaining elements into two parts. If we delete the elements nums[2] = 5 and nums[3] = 8, the remaining elements are [7,9,1,3]. The difference between and is (7 + 9) - (1 + 3) = 12. In order to get the minimum difference, we should delete nums[1] = 9 and nums[4] = 1, and the remaining elements are [7,5,8,3]. The difference between and is (7 + 5) - (8 + 3) = 1. Observation shows that the best answer is 1.
Tips:
- nums.length == 3 * n
- 1 <= n <= 105
- 1 <= nums[i] <= 105
Idea: the chicken in this dish is really afraid of difficulties. It took ten minutes to have the first version of immature ideas. The idea at that time was to assume that the midpoint of the remaining 2n numbers after deletion must be in the range of n-2n in the original 3n length array. Therefore, the original array is divided into [n,2n], [n + 1,2n-1], [2n,n]. Then sort them separately. For the first half, leave the minimum n number, and for the second half, leave the maximum n number. Finally, filter out a maximum value. In fact, when I wrote it out at that time, I knew it was not feasible. The complexity came to the amazing O(n*n*logn). There could be no drama for the example of 10 ^ 5, but I really had no ideas and had to bite the bullet. Finally, it timed out. At this time, there are about 20 minutes left. There is no achievement behind. Give up in the last five minutes and wait for the answer.
class Solution {
public long minimumDifference(int[] nums) {
int n = nums.length / 3;
long res = 0;
int[] arr1 = Arrays.copyOfRange(nums, 0, n);
int[] arr2 = Arrays.copyOfRange(nums, n, nums.length);
int sum1 = 0;
int sum2 = 0;
Arrays.sort(arr1);
Arrays.sort(arr2);
for (int j = 0; j < n; j++) {
sum1 += arr1[j];
}
for (int j = n; j < 2 * n; j++) {
sum2 += arr2[j];
}
res = sum1 - sum2;
for (int i = n + 1; i <= 2 * n; i++) {
arr1 = Arrays.copyOfRange(nums, 0, i);
arr2 = Arrays.copyOfRange(nums, i, nums.length);
Arrays.sort(arr1);
Arrays.sort(arr2);
sum1 = 0;
sum2 = 0;
for (int j = 0; j < n; j++) {
sum1 += arr1[j];
}
for (int j = arr2.length - n; j < arr2.length; j++) {
sum2 += arr2[j];
}
res = Math.min(res, sum1 - sum2);
}
return res;
}
}Follow up: still reference arignote For the answer of the boss, two priority queues can be used to record the numbers retained by the arrays on both sides. According to the analysis of the above ideas, the position of the segmentation point in the original array must be within the range of [n,2n]. Therefore, each time you calculate within this range, you can get the minimum value. For more specific instructions, please refer to the problem solution.
class Solution {
public long minimumDifference(int[] nums) {
long left[] = new long[nums.length + 1], right[] = new long[nums.length + 1], min = Long.MAX_VALUE;
PriorityQueue<Integer> leftQueue = new PriorityQueue<>(), rightQueue = new PriorityQueue<>();
for (int i = 0; i < nums.length; i++) {
leftQueue.offer(-nums[i]);
left[i + 1] = left[i] + nums[i] + (leftQueue.size() > nums.length / 3 ? leftQueue.poll() : 0);
}
for (int i = nums.length - 1; i >= 0; i--) {
rightQueue.offer(nums[i]);
right[i] = right[i + 1] + nums[i] - (rightQueue.size() > nums.length / 3 ? rightQueue.poll() : 0);
}
for (int i = nums.length / 3; i <= 2 * nums.length / 3; i++) {
min = Math.min(min, left[i] - right[i]);
}
return min;
}
}summary
This is the second time for this dish chicken to participate in the competition. Of course, it still focuses on participation. However, the first three questions are still relatively smooth. After careful consideration of the fourth question, it should be said that there is no problem, but it is not sensitive to the commonly used data structure. If you can quickly think of heap or priority queue, you may be able to win this question. In general, there are several cases stuck in question 3 for the first time, which is still some progress. Anyway, keep trying.