Catalogue of series articles
I Array type problem solving method 1: dichotomy
II Array type problem solving method 2: Double finger needle method
III Array type problem solving method 3: sliding window
IV Array type problem solving method 4: simulation
V The basic operation and classic topics of the linked list
Vi Classic title of hash table
VII Classic title of string
VIII KMP of string
IX Solution: double pointer
X Classic title of stack and queue
Xi top-K problem in stack and queue
XII The first, middle and last order traversal of binary tree
XIII Sequence traversal of binary tree and related topics
XIV Binary tree part of binary tree attributes related topics
XV Modification and construction of binary tree in binary tree chapter
XVI Properties of binary search tree
XVII The problem of common ancestor in binary tree discourse
XVIII Modification and construction of binary search tree in binary tree chapter
Updating
preface
The question brushing route comes from: Code Capriccio
Combinatorial problem: find the set of k numbers according to certain rules in N numbers
Backtracking algorithm is a pure violent search method, which is a kind of DFS (depth first search) in tree structure. It is used to solve some problem types that can not be written by normal violent solutions due to the change of the number of layers of the cycle. It is also an exhaustive list of all results, but pruning can be carried out in the process.
In backtracking algorithms, global variables are usually used to record paths and states. For the path and state recorded in the process of downward recursion, after a path recursion is completed and the lower recursion returns to the upper recursion, it is necessary to backtrack (return the state to before entering the lower recursion).
Inscription
77. Portfolio
Leetcode link
Given two integers n and k, returns the combination of all possible k numbers in the range [1, n]. You can return answers in any order.

Solution:
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combine(int n, int k) {
backtracking(n, k, 1);
return res;
}
public void backtracking(int n, int k, int start) {
// End condition: path size() == k
if (path.size() == k) {
// Add to result set and return
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i <= n; i++) {
path.add(i);
// Because integers cannot be repeated, the lower level recursion needs to start from the starting position i of this level recursion plus one position
backtracking(n, k, i + 1);
// Backtracking to remove the value added before this recursion
path.remove(path.size() - 1);
}
}
}
Pruning Optimization:
Number of stored elements: path size()
You also need to find the number of elements: K - path size()
The starting position can be traversed at most from: n - (k - path.size()) + 1
...
for (int i = start; i <= n - (k - path.size()) + 1; i++) {
...
}
216. Combined sum III
Leetcode link
Find the combination of all k numbers whose sum is n. Only positive integers of 1 - 9 are allowed in the combination, and there are no duplicate numbers in each combination.

Solution:
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int sum = 0;
public List<List<Integer>> combinationSum3(int k, int n) {
backtracking(k, n, 1);
return res;
}
public void backtracking(int k, int n, int start) {
// End condition
if (path.size() > k || sum > n) {
// And is greater than n or the number of elements collected is greater than k
return;
}
if (path.size() == k && sum == n) {
// The number of k has been collected, and the sum is equal to n
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i <= 9 - (k - path.size()) + 1; i++) {
path.add(i);
sum += i;
// The number is not repeated, and the next round of recursion starts from i + 1
backtracking(k, n, i + 1);
// Both sum and path should be traced back
path.remove(path.size() - 1);
sum -= i;
}
}
}
Save sum without using global variables, hide backtracking as recursive parameters, and make the code more concise
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum3(int k, int n) {
int sum = 0;
backtracking(k, n, 1, sum);
return res;
}
public void backtracking(int k, int n, int start, int sum) {
if (path.size() > k || sum > n) {
return;
}
if (path.size() == k && sum == n) {
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i <= 9 - (k - path.size()) + 1; i++) {
path.add(i);
//sum += i;
// Pass sum + i as a parameter into the lower level recursion
backtracking(k, n, i + 1, sum + i);
path.remove(path.size() - 1);
// When sum + i is taken as the parameter, the sum of this layer does not change, and there is no need to backtrack after returning to this layer
//sum -= i;
}
}
}
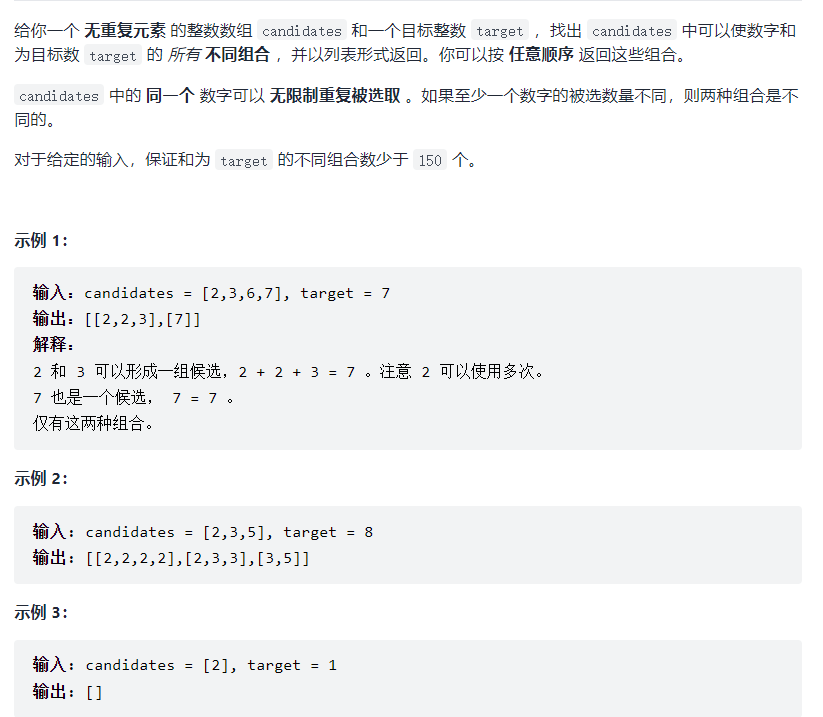
39. Combination sum
Leetcode link
Solution:
For the sake of code simplicity, sum is still placed in recursive parameters
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
backtracking(candidates, target, 0, 0);
return res;
}
public void backtracking(int[] nums, int target, int start, int sum) {
if (sum > target) {
return;
}
if (sum == target) {
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i < nums.length; i++) {
path.add(nums[i]);
// A number can be used multiple times, and the subscript i is added by one
backtracking(nums, target, i, sum + nums[i]);
path.remove(path.size() - 1);
}
}
}
40. Combined sum II
Leetcode link
Given a candidate number set candidates and a target number target, find out all combinations in candidates that can make the sum of numbers target. Each number in candidates can only be used once in each combination.
Note: the solution set cannot contain duplicate combinations.

Solution:
Sort first, you can put the same numbers together
Because there are duplicate numbers in the array, duplicate combinations are not allowed in the second return list, such as:
Array: num [1, 1, 2, 3] target = 4
[1, 3] and [1, 3]. Since the second 1 is repeated with the previous 1, the second [1, 3] obviously needs pruning, but the half segment condition cannot only have nums [I - 1] = nums [i]. Look at [1, 1, 2]. When the first 1 enters the second layer of recursion, the second 1 here is useful, because the 1 here is the starting position of this layer of recursion
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
// sort
Arrays.sort(candidates);
backtracking(candidates, target, 0, 0);
return res;
}
public void backtracking(int[] nums, int target, int start, int sum) {
// The end condition here is placed in the for loop judgment condition of the upper layer, which simplifies the code and reduces the number of recursion
// if (sum > target) {
// return;
// }
// End condition
if (sum == target) {
// Add and return
res.add(new ArrayList<>(path));
return;
}
for (int i = start; i < nums.length && sum + nums[i] <= target; i++) {
if (i > start && nums[i] == nums[i - 1]) {
// It is not the starting position. If it is repeated with the previous number, skip directly
continue;
}
path.add(nums[i]);
backtracking(nums, target, i + 1, sum + nums[i]);
// to flash back
path.remove(path.size() - 1);
}
}
}
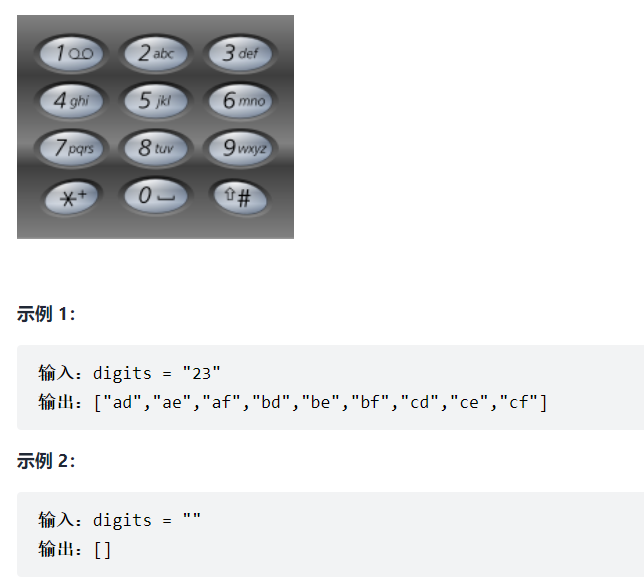
17. Letter combination of telephone number
Leetcode link
Given a string containing only numbers 2-9, returns all the letter combinations it can represent. The answers can be returned in any order. The mapping of numbers to letters is given as follows (the same as telephone keys). Note that 1 does not correspond to any letter.
Solution:
- The array holds the mapping relationship between numbers and strings
- The recursive string of each layer is related to the depth of recursion, and the depth of recursion is determined by the subscript of digits, so the parameter list needs a deep to record
- Before each traversal, you need to get the string to be traversed by the recursion of this layer, that is, the mapping string of the number corresponding to the depth of recursion
class Solution {
List<String> res = new ArrayList<>();
// sb here can also be used as a recursive parameter to hide backtracking
StringBuilder sb = new StringBuilder();
public List<String> letterCombinations(String digits) {
if (digits.equals("") || digits == null) {
return res;
}
// Array save mapping relationship
String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
backtracking(digits, numString, 0);
return res;
}
public void backtracking(String digits, String[] numString, int deep) {
// End condition
if (deep == digits.length()) {
// Add to result set and return
res.add(sb.toString());
return;
}
// The mapping array starts with the 0 subscript, digits Charat (deep) gets the character form of numbers,
// digits.charAt(deep) - '0' gets the corresponding subscript
String s = numString[digits.charAt(deep) - '0'];
for (int i = 0; i < s.length(); i++) {
sb.append(s.charAt(i));
backtracking(digits, numString, deep + 1);
// to flash back
sb.deleteCharAt(sb.length() - 1);
}
}
}
summary
Backtracking template:
public void backtracking(parameter) {
if (Termination conditions) {
// Store results and return
Add to return list;
return;
}
if (Other termination conditions) {
// Return directly, or put it into the for loop for judgment
return;
}
for (Selection: Elements in the collection of this layer (the number of node children in the tree is the size of the collection)) {
Processing node;
backtracking(Path, selection list);
Backtracking, undo processing results;
}
}
- The returned list is generally used as a global variable, because it is concise and reduces the recursive parameter list
- Similar to sum and string, which need to be dynamically maintained and backtracked in the recursive process, in addition to being used as global variables, they can also be used as recursive parameters to hide backtracking.
- Pruning usually modifies the end condition of the for loop, similar to the above questions