1. Title

Merge the two ascending linked lists into a new ascending linked list and return the head node of the linked list. The new linked list is composed of all nodes of a given two linked lists.

1.1 example

• Example 1 1 1 :

• Input: list1 = [1, 2, 4], list2 = [1, 3, 4];
• Output: [1, 1, 2, 3, 4, 4].

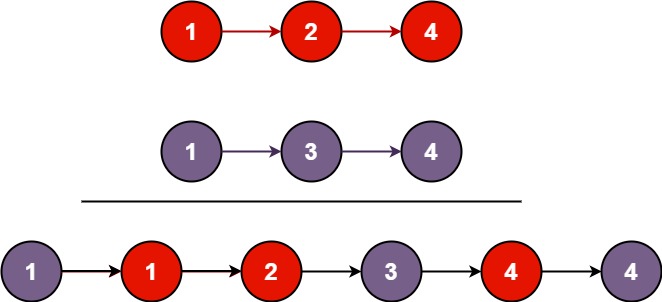
• Example 2 2 2 :

• Input: list1 = [], list2 = [];
• Output: [].

• Example 3 3 3 :

• Input: list1 = [], list2 = [0];
• Output: [0].

1.2 description

• Source: LeetCode
• Link: https://leetcode-cn.com/problems/merge-two-sorted-lists/

1.3 restrictions

• -100 <= Node.val <= 100 ；
• The number range of nodes of the two linked lists is [0, 50];
• list1 and list2 are arranged in non decreasing order.

2. Solution I (iterative method)

2.1 analysis

The iterative method is very simple to solve this problem, which is used below 3 3 Three auxiliary cursor variables: cursor, cursor1 and cursor2 are used to indicate the node position in the merged linked list, the first given linked list and the second given linked list respectively during the iteration process.

2.2 answers

from typing import Optional


class ListNode:
    def __init__(self, val=0, nxt=None):
        self.val = val
        self.nxt = nxt


class Solution:
    def merge2lists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        if not list1:
            return list2
        if not list2:
            return list1
        cursor1, cursor2 = list1, list2
        if cursor1.val < cursor2.val:
            merged_list = ListNode(cursor1.val)
            cursor1 = cursor1.nxt
        else:
            merged_list = ListNode(cursor2.val)
            cursor2 = cursor2.nxt
        cursor = merged_list
        while cursor1 and cursor2:
            if cursor1.val < cursor2.val:
                cursor.nxt = ListNode(cursor1.val)
                cursor1 = cursor1.nxt
            else:
                cursor.nxt = ListNode(cursor2.val)
                cursor2 = cursor2.nxt
            cursor = cursor.nxt
        if cursor1:
            cursor.nxt = cursor1
        if cursor2:
            cursor.nxt = cursor2
        return merged_list


def main():
    node6 = ListNode(val=4)
    node5 = ListNode(val=3)
    node4 = ListNode(val=1)
    node4.nxt, node5.nxt = node5, node6
    node3 = ListNode(val=4)
    node2 = ListNode(val=2)
    node1 = ListNode(val=1)
    node1.nxt, node2.nxt = node2, node3
    list1, list2 = node1, node4
    sln = Solution()
    merged_list = sln.merge2lists(list1, list2)
    cursor = merged_list
    while cursor:
        print(cursor.val)
        cursor = cursor.nxt


if __name__ == '__main__':
    main()

It should be noted that in the above code, when each iteration of the while loop is completed, the cursor cursor needs to be moved every time except cursor1 or cursor2 cursor according to the conditions.

The test run results of the above code are as follows:

1
1
2
3
4
4

2.3 complexity

• Time complexity: O ( n + m ) O(n+m) O(n+m), where n n n and m m m is the length of the two linked lists respectively. Because only one element of list1 and list2 will be put into the combined linked list in each loop iteration, the number of while loops will not exceed the sum of the lengths of the two linked lists. The time complexity of all other operations is constant, so the total time complexity is O ( n + m ) O(n+m) O(n+m) ；
• Space complexity: O ( 1 ) O(1) O(1) . Only constant space is needed to store several variables.

Although the time and space complexity of the above solutions are excellent, the code is a little verbose and not elegant, because a special code segment is used to process the header node of the merged linked list. In fact, a dummy node can be used to optimize it as follows:

from typing import Optional


class ListNode:
    def __init__(self, val=0, nxt=None):
        self.val = val
        self.nxt = nxt


class Solution:
    def merge2lists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        # A dummy.next node to store the result
        dummy = ListNode(-sys.maxsize)
        cursor = dummy
        while True:
            # If any of the list gets completely empty
            # directly join all the elements of the other list
            if list1 is None:
                cursor.next = list2
                break
            if list2 is None:
                cursor.next = list1
                break
                
            # Compare the data of the lists and whichever is smaller is
            # appended to the last of the merged list and the head is changed
            if list1.val <= list2.val:
                cursor.next = list1
                list1 = list1.next
            else:
                cursor.next = list2
                list2 = list2.next
    
            # Advance the cursor
            cursor = cursor.next
    
        # Returns the head of the merged list
        return dummy.next

3. Solution II (recursive method)

3.1 analysis

In addition to the above iterative solution, the recursive solution shown below can also be used for this problem. Although the recursive solution is simpler, it is also less easy to understand.

3.2 answers

from typing import Optional


class ListNode:
    def __init__(self, val=0, nxt=None):
        self.val = val
        self.nxt = nxt


class Solution:
    def recursive_merge2lists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        if not list1:
            return list2
        if not list2:
            return list1
        if list1.val < list2.val:
            head = list1
            head.nxt = self.recursive_merge2lists(list1.nxt, list2)
        else:
            head = list2
            head.nxt = self.recursive_merge2lists(list1, list2.nxt)
        return head


def main():
    node6 = ListNode(val=4)
    node5 = ListNode(val=3)
    node4 = ListNode(val=1)
    node4.nxt, node5.nxt = node5, node6
    node3 = ListNode(val=4)
    node2 = ListNode(val=2)
    node1 = ListNode(val=1)
    node1.nxt, node2.nxt = node2, node3
    list1, list2 = node1, node4
    sln = Solution()
    merged_list = sln.recursive_merge2lists(list1, list2)
    cursor = merged_list
    while cursor:
        print(cursor.val)
        cursor = cursor.nxt


if __name__ == '__main__':
    main()

3.3 complexity

• Time complexity: O ( n + m ) O(n+m) O(n+m), where n n n and m m m is the length of the two linked lists respectively. Because the head node of list1 or list2 will be removed every time recursion is called (until at least one linked list is empty), the method recursive_merge2lists calls each node recursively at most once. Therefore, the time complexity depends on the length of the combined linked list, i.e O ( n + m ) O(n+m) O(n+m) ；
• Space complexity: O ( n + m ) O(n+m) O(n+m), where n n n and m m m is the length of the two linked lists respectively. Recursive call recursive_ The merge2lists method consumes stack space, which depends on the depth of recursive calls. Recursive at end of recursive call_ The merge2lists method is called at most n + m n+m n+m times, so the spatial complexity is O ( n + m ) O(n+m) O(n+m) .