Give you the head node of the linked list. Please arrange it in ascending order and return the sorted linked list.

Example 1:

 

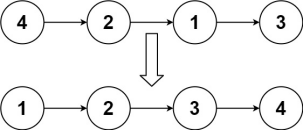
Input: head = [4,2,1,3] output: [1,2,3,4]

Example 2:

 

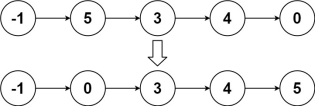
Input: head = [-1,5,3,4,0] output: [- 1,0,3,4,5]

Example 3:

Input: head = [] output: []

Idea:

At first glance, this problem is to sort the linked list. It seems that I have never touched on how to sort the linked list before. Can I sort it with the sorting method like sorting ordinary arrays? Yes.

Here we can use the idea of merging and sorting to solve it. Merging and sorting is still a recursive method. The general idea is to divide the array to be sorted into two parts, merge and sort the two parts, and then merge the two ordered arrays together. This problem can be solved as long as the base case for merging and sorting is defined (for example, it is returned directly when the number is 1).

If there is a basis for merging and sorting, what is written above is easy to understand. Now the problem turns to: how to similarly divide the linked list into two parts when merging and sorting on the linked list? Use the speed pointer. Although we don't know the length of the linked list, we define a slow pointer that takes one step at a time and a fast pointer that takes two steps at a time. When the fast pointer reaches the end point, the position of the full pointer is the middle syncopation point!

How to define base case? We continue to merge and sort the separated parts. When there is only one node or the incoming node is empty, we don't need to be divided into two parts. Just return to the current one, which is the base case.

So how to merge the sorted two parts? Isn't this the problem of merging two ordered linked lists? Here I use the non recursive method to open up the third result linked list, and add the smaller values in the two linked lists to the result linked list one by one. Because this is not the focus of this problem, the specific details are no longer described, but can be reflected in the code.

code:

class Solution(object):

    def sortList(self, head):

        def merge_sort(head):#merge_ The sort function is to merge and sort the incoming linked list and return the sorted results

            #Define base case

            if not head or not head.next:#If empty, or only one node

                return head#Return directly to yourself

            slow,fast=head,head.next#fast is initialized to head Next, if head is initialized, the loop will be closed

                #fast is initialized to head Next can also ensure that slow reaches the end of the first half of the paragraph anyway

            while fast and fast.next:#The judgment of the fast pointer is the same as that of the ring linked list

                slow=slow.next#Slow the pointer one step

                fast=fast.next.next#Come on, take two steps

            #Now the slow pointer comes to the end of the first part

            head2 = slow.next#The next node of the slow pointer is regarded as the new header node head2

            slow.next=None#The slow pointer points to null to make the first part of the linked list independent

            return merge(merge_sort(head),merge_sort(head2))#The two parts are sorted separately and then merge d

        def merge(root1,root2):#merge method, merging two ordered linked lists

            p = ListNode()#Define the third linked list

            q = p#q temporary header node

            while root1  and root2:#The two pointers swim in the two linked lists respectively, and take the small one and put it into the third linked list

                if root1.val<=root2.val:#root1 small

                    p.next=root1

                    p=p.next

                    root1= root1.next

                else:#root2 small

                    p.next=root2

                    p=p.next

                    root2 = root2.next

            p.next=root1 if root1 else root2#Add all the remaining parts of the linked list that have not been traversed into the result

            return q.next

        return merge_sort(head)

Summary:

From the perspective of recursive functions as a whole, merge_sort first uses the fast and slow pointer to divide the linked list into two parts. After merging and sorting respectively, merge the results and return to the sorted head node. The logic is self consistent and does not need to jump into the next layer of recursion. Everything is naturally left to automatic recursion and base case.

The details to pay attention to in implementation include the initialization of fast pointer, which should be initialized to head Next, which can ensure that when fast reaches the end point (the final node or the next bit of the final node), the position of slow is at the end of the first half. This small conclusion is summarized due to the error of the result (real knowledge comes from practice). You can understand it by drawing the figure below yourself.