1. Introduction
- Graph: directed graph and undirected graph
- Problem solving steps:
(1) Drawing construction: what kind of drawing and how to build it
(2) Then, specific problems are analyzed, such as using BFS and greedy algorithm to operate the graph
- Joint search set
//Parallel query set (manage a series of sets that do not want to be intersected), with the functions of query and consolidation
class DisjointSetUnion {
int[] f;//Stores the parent node of each element
int[] rank;//Record the depth of the tree corresponding to each root node
int n;
public DisjointSetUnion(int n) {
this.n = n;
this.rank = new int[n];//Record the depth of the tree corresponding to each root node
this.f = new int[n];//Stores the parent node of each element
for (int i = 0; i < n; i++) {
this.rank[i] = 1;//The initial value is set to 1
this.f[i] = i;//Set the parent node as yourself at the beginning
}
}
//Compressed path query method, recursive implementation
//Access the parent node layer by layer until the root node (the flag of the root node is that the parent node is itself). To judge whether two elements belong to the same set, you only need to see whether their root nodes are the same
public int find(int x) {
return f[x] == x ? x : (f[x] = find(f[x]));
}
//Merge method
public boolean unionSet(int x, int y) {
int fx = find(x), fy = find(y);//Find the root node of the two nodes
if (fx == fy) {//The root nodes of the two nodes are the same without merging
return false;
}
if (rank[fx] < rank[fy]) {//The depth of the tree with fx as the root node is less than that of the tree with fy as the root node
f[fx] = fy;
} else if (rank[fx] > rank[fy]) {
f[fy] = fx;
} else {
f[fx] = fy;
rank[fy] += 1;
}
return true;
}
}
2. Programming questions
2.1 127. Word Chain
The conversion sequence from the words beginWord and endWord in the dictionary wordList is a sequence formed according to the following specifications:
The first word in the sequence is beginWord.
The last word in the sequence is endWord.
Only one letter can be changed at a time.
The intermediate word in the conversion process must be a word in the dictionary wordList.
Give you two words beginWord and endWord and a dictionary wordList to find the number of words in the shortest conversion sequence from beginWord to endWord. If there is no such conversion sequence, 0 is returned.
1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord, endWord, and wordList[i] are composed of lowercase English letters
beginWord != endWord
All strings in wordList are different from each other
- Create diagram
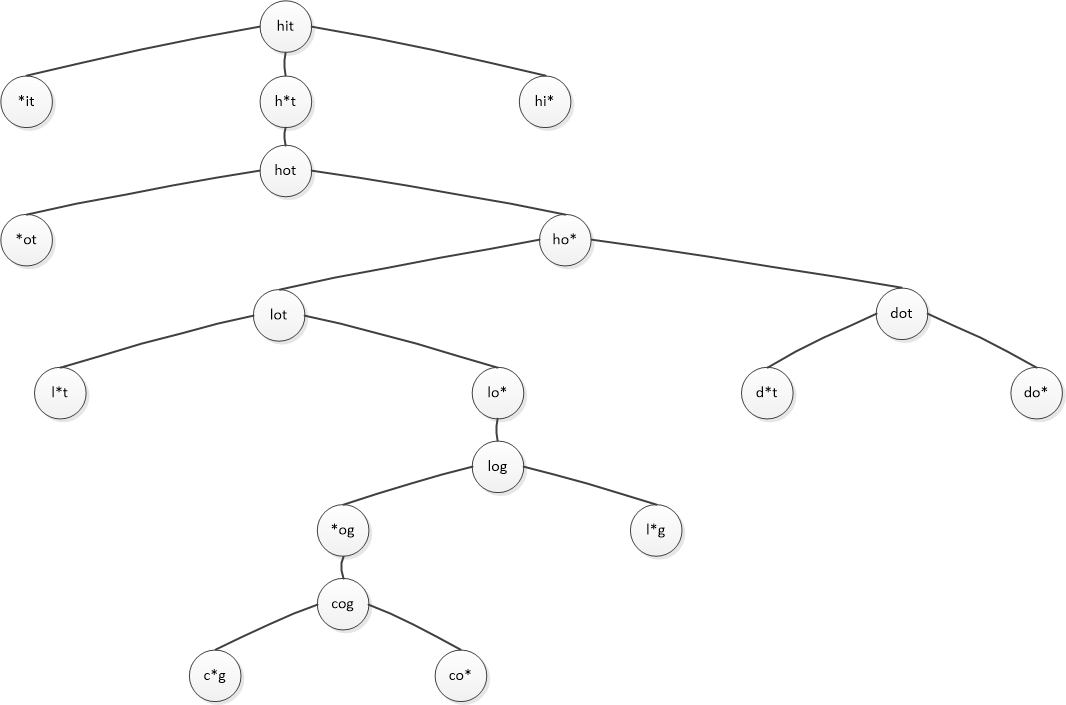
/*
1.Assign an Id to each word and use hashmap to store it
2.Mapping
3.Breadth first search
*/
class Solution {
Map<String,Integer> wordId = new HashMap<>();//Id of the saved word
List<List<Integer>> edge = new ArrayList<>();//Save edges of graph
int nodeNum = 0;//Word id
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
//Create diagram
for(String word : wordList){
addEdge(word);
}
addEdge(beginWord);
//non-existent
if(!wordId.containsKey(endWord)) return 0;
int[] dis = new int[nodeNum];//Distance from starting point to each node
Arrays.fill(dis,Integer.MAX_VALUE);//Initialize to the maximum value. If the current value is the maximum value during search, it indicates that this node has not been accessed
int beginId = wordId.get(beginWord);
int endId = wordId.get(endWord);
dis[beginId] = 0;//The distance from the starting point is 0
//Breadth first search
Queue<Integer> que = new LinkedList<>();
que.offer(beginId);
while(!que.isEmpty()){
int cur = que.poll();
if(cur == endId){
return dis[endId] / 2 + 1;
/*
Because the virtual node is added, the distance we get is twice the actual shortest path length.
At the same time, we do not calculate the contribution of the starting point to the answer, so we should return the result of half the distance plus one.
*/
}
for(int curNext : edge.get(cur)){
if(dis[curNext] == Integer.MAX_VALUE){
dis[curNext] = dis[cur] + 1;
que.offer(curNext);
}
}
}
return 0;
}
//Create edge
//For example, hot connection: * ot, h*t, ho*
private void addEdge(String word){
addWord(word);
int id1 = wordId.get(word);
char[] array = word.toCharArray();
int length = array.length;
for(int i=0;i<length;++i){
char temp = array[i];
array[i] = '*';
String newWord = new String(array);
addWord(newWord);
int id2 = wordId.get(newWord);
edge.get(id1).add(id2);
edge.get(id2).add(id1);
array[i] = temp;
}
}
//Add word id
private void addWord(String word){
if(!wordId.containsKey(word)){
wordId.put(word,nodeNum++);
edge.add(new ArrayList<Integer>());
}
}
}
- Optimization: bidirectional breadth first search
class Solution {
Map<String, Integer> wordId = new HashMap<String, Integer>();
List<List<Integer>> edge = new ArrayList<List<Integer>>();
int nodeNum = 0;
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
for (String word : wordList) {
addEdge(word);
}
addEdge(beginWord);
if (!wordId.containsKey(endWord)) {
return 0;
}
int[] disBegin = new int[nodeNum];
Arrays.fill(disBegin, Integer.MAX_VALUE);
int beginId = wordId.get(beginWord);
disBegin[beginId] = 0;
Queue<Integer> queBegin = new LinkedList<Integer>();
queBegin.offer(beginId);
int[] disEnd = new int[nodeNum];
Arrays.fill(disEnd, Integer.MAX_VALUE);
int endId = wordId.get(endWord);
disEnd[endId] = 0;
Queue<Integer> queEnd = new LinkedList<Integer>();
queEnd.offer(endId);
while (!queBegin.isEmpty() && !queEnd.isEmpty()) {
int queBeginSize = queBegin.size();
for (int i = 0; i < queBeginSize; ++i) {
int nodeBegin = queBegin.poll();
if (disEnd[nodeBegin] != Integer.MAX_VALUE) {
return (disBegin[nodeBegin] + disEnd[nodeBegin]) / 2 + 1;
}
for (int it : edge.get(nodeBegin)) {
if (disBegin[it] == Integer.MAX_VALUE) {
disBegin[it] = disBegin[nodeBegin] + 1;
queBegin.offer(it);
}
}
}
int queEndSize = queEnd.size();
for (int i = 0; i < queEndSize; ++i) {
int nodeEnd = queEnd.poll();
if (disBegin[nodeEnd] != Integer.MAX_VALUE) {
return (disBegin[nodeEnd] + disEnd[nodeEnd]) / 2 + 1;
}
for (int it : edge.get(nodeEnd)) {
if (disEnd[it] == Integer.MAX_VALUE) {
disEnd[it] = disEnd[nodeEnd] + 1;
queEnd.offer(it);
}
}
}
}
return 0;
}
public void addEdge(String word) {
addWord(word);
int id1 = wordId.get(word);
char[] array = word.toCharArray();
int length = array.length;
for (int i = 0; i < length; ++i) {
char tmp = array[i];
array[i] = '*';
String newWord = new String(array);
addWord(newWord);
int id2 = wordId.get(newWord);
edge.get(id1).add(id2);
edge.get(id2).add(id1);
array[i] = tmp;
}
}
public void addWord(String word) {
if (!wordId.containsKey(word)) {
wordId.put(word, nodeNum++);
edge.add(new ArrayList<Integer>());
}
}
}
2.2 207. Class Schedule Card
You must take numCourses this semester, marked 0 to numCourses - 1.
Some prerequisite courses are required before taking some courses. Prerequisite courses are given by the array prerequisites, where prerequisites[i] = [ai, bi], which means that if you want to learn course ai, you must learn course bi first.
For example, the prerequisite course pair [0, 1] indicates that if you want to learn course 0, you need to complete course 1 first.
Please judge whether it is possible to complete all courses? If yes, return true; Otherwise, false is returned.
1 <= numCourses <= 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
All course pairs in prerequisites[i] are different from each other
//Topological sorting
class Solution {
List<List<Integer>> edges = new ArrayList<>();//Stored directed graph
int[] indeg;//Stores the in degree value of the current node, that is, the number of parent nodes of the current node
public boolean canFinish(int numCourses, int[][] prerequisites) {
// Mapping
// A total of lists equal to the number of courses have been created
// The subscript of each list corresponds to each course
// The value stored in each list is the next course that the course points to
for (int i = 0; i< numCourses; ++i) {
edges.add(new ArrayList<Integer>());
}
// Create a rating table
// The array subscript corresponds to the corresponding course, and the value in it is the entry value of the course
indeg = new int[numCourses];
for (int[] prerequisite : prerequisites) {
edges.get(prerequisite[1]).add(prerequisite[0]);
++indeg[prerequisite[0]];
}
// Breadth first search
Queue<Integer> que = new LinkedList<>();
// Nodes with the entry value of 0 enter the queue first, that is, only after learning these courses can they learn the next courses
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0){
que.offer(i);
}
}
int visited = 0;//Record the number of accessed nodes
while (!que.isEmpty()) {
++visited;
int course = que.poll();//Get the node with the penetration value of 0
for (int courseNext : edges.get(course)) {
--indeg[courseNext];
if (indeg[courseNext] == 0){//Join the queue when the entry value is 0
que.offer(courseNext);
}
}
}
//If the number of access nodes is the same as the number of courses, it means that all courses can be completed
return visited == numCourses;
}
}
2.3 210. Schedule II
Now you have a total of numCourses to choose, which are recorded as 0 to numCourses - 1. Give you an array of prerequisites, where prerequisites[i] = [ai, bi], indicating that bi must be selected before taking the elective course ai.
For example, to learn course 0, you need to complete course 1 first. We use a match to represent: [0,1].
Return to the learning sequence you arranged to complete all courses. There may be multiple correct orders. You just need to return any one. If it is not possible to complete all courses, an empty array is returned.
1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
All [ai, bi] are different from each other
//Topological sorting
class Solution {
List<List<Integer>> edges = new ArrayList<>();//Stored directed graph
int[] indeg;//Stores the in degree value of the current node, that is, the number of parent nodes of the current node
public int[] findOrder(int numCourses, int[][] prerequisites) {
// Mapping
// A total of lists equal to the number of courses have been created
// The subscript of each list corresponds to each course
// The value stored in each list is the next course that the course points to
for (int i = 0; i< numCourses; ++i) {
edges.add(new ArrayList<Integer>());
}
// Create a rating table
// The array subscript corresponds to the corresponding course, and the value in it is the entry value of the course
indeg = new int[numCourses];
for (int[] prerequisite : prerequisites) {
edges.get(prerequisite[1]).add(prerequisite[0]);
++indeg[prerequisite[0]];
}
// Breadth first search
Queue<Integer> que = new LinkedList<>();
// Nodes with the entry value of 0 enter the queue first, that is, only after learning these courses can they learn the next courses
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0){
que.offer(i);
}
}
int[] ans = new int[numCourses];
int index = 0;
while (!que.isEmpty()) {
int course = que.poll();//Get the node with the penetration value of 0
ans[index++] = course;
for (int courseNext : edges.get(course)) {
--indeg[courseNext];
if (indeg[courseNext] == 0){//Join the queue when the entry value is 0
que.offer(courseNext);
}
}
}
if (index != numCourses) {//It means that you can't complete all courses
return new int[0];
}
return ans;
}
}
2.4 399. Division evaluation
Give you a variable pair array equations and a real value array values as known conditions, where equations[i] = [Ai, Bi] and values[i] jointly represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string representing a single variable.
There are also some problems represented by array queries, where queries[j] = [Cj, Dj] represents the j-th problem. Please find Cj / Dj =? As the answer.
Return answers to all questions. If there is an uncertain answer, replace it with - 1.0. If there is a string in the question that does not appear in the given known conditions, you also need to replace the answer with - 1.0.
Note: input is always valid. You can assume that there will be no divisor of 0 in the division operation, and there are no contradictory knots
1 <= equations.length <= 20
equations[i].length == 2
1 <= Ai.length, Bi.length <= 5
values.length == equations.length
0.0 < values[i] <= 20.0
1 <= queries.length <= 20
queries[i].length == 2
1 <= Cj.length, Dj.length <= 5
AI, Bi, CJ and DJ are composed of lowercase English letters and numbers
/*
1.Character mapping to integer
2.Mapping (undirected graph)
3.Traverse the problem and conduct breadth first search for each problem
*/
class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
int nvars = 0;//Characters are mapped to integers
Map<String,Integer> variables = new HashMap<>();
int n = equations.size();
//Map different strings in the equations array to integers
for (int i = 0; i < n; ++i) {
if (!variables.containsKey(equations.get(i).get(0))) {
variables.put(equations.get(i).get(0),nvars++);
}
if (!variables.containsKey(equations.get(i).get(1))) {
variables.put(equations.get(i).get(1),nvars++);
}
}
//Mapping
List<List<Pair>> edges = new ArrayList<>();//For each point, all points directly connected to it and their corresponding weights are stored
for (int i = 0; i < nvars; ++i) {
edges.add(new ArrayList<Pair>());
}
for ( int i = 0; i < n; ++i) {
int va = variables.get(equations.get(i).get(0));//The integer mapped by the divisor
int vb = variables.get(equations.get(i).get(1));//Integer mapped by divisor
edges.get(va).add(new Pair(vb,values[i]));
edges.get(vb).add(new Pair(va,1.0/values[i]));
}
int queriesCount = queries.size();
double[] ret = new double[queriesCount];//Store results
//The traversal problem is solved
for (int i = 0; i < queriesCount; ++i) {
List<String> query = queries.get(i);
double result = -1.0;
if (variables.containsKey(query.get(0)) && variables.containsKey(query.get(1))) {//If the character in the problem exists in the map
int ia = variables.get(query.get(0));
int ib = variables.get(query.get(1));
if (ia == ib) {//If the divisor and the divisor are equal, the quotient is 1.0
result = 1.0;
} else { // Unequal
//Breadth first search
Queue<Integer> points = new LinkedList<>();
points.offer(ia);
double[] ratios = new double[nvars];//Store the value of ia/i
Arrays.fill(ratios,-1.0);//Initialize to - 1.0 because some answers cannot be determined
ratios[ia] = 1.0;// ia/ia = 1.0
while (!points.isEmpty() && ratios[ib] < 0) {
int x = points.poll();
for (Pair pair : edges.get(x)) {
int y = pair.index;
double val = pair.value;// Weight, i.e. the value of x/y
if (ratios[y] < 0) {
ratios[y] = ratios[x] * val;// I.e. ia/y = (ia/x) * (x/y);
points.offer(y);
}
}
}
result = ratios[ib];
}
}
ret[i] = result;
}
return ret;
}
}
//Weighted node
class Pair {
int index;//Index of current node
double value;//Weight: the ratio of the parent node index to the current node index
Pair(int index,double value) {
this.index = index;
this.value = value;
}
}
2.5 1584. Minimum cost of connecting all points
Give you an array of points to represent some points on the 2D plane, where points[i] = [xi, yi].
The cost of connecting point [xi, yi] and point [xj, yj] is the Manhattan distance between them: |xi - xj| + |yi - yj|, where | val | represents the absolute value of val.
Please return the minimum total cost of connecting all points. All points are considered connected only if there is and only one simple path between any two points.
1 <= points.length <= 1000
-106 <= xi, yi <= 106
All points (xi, yi) are different.
Detailed collection and investigation
//Kruskal algorithm
class Solution {
public int minCostConnectPoints(int[][] points) {
int n = points.length;
DisjointSetUnion dsu = new DisjointSetUnion(n);
//Build a map and connect all points
List<Edge> edges = new ArrayList<Edge>();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
edges.add(new Edge(dist(points, i, j), i, j));
}
}
//According to the distance between two points, sort from small to large, greedy algorithm: select the minimum edge to join each time
Collections.sort(edges, new Comparator<Edge>() {
public int compare(Edge edge1, Edge edge2) {
return edge1.len - edge2.len;
}
});
int ret = 0, num = 1;
for (Edge edge : edges) {
int len = edge.len, x = edge.x, y = edge.y;
if (dsu.unionSet(x, y)) {
ret += len;
num++;
if (num == n) {
break;
}
}
}
return ret;
}
//Calculate the distance between two points
public int dist(int[][] points, int x, int y) {
return Math.abs(points[x][0] - points[y][0]) + Math.abs(points[x][1] - points[y][1]);
}
}
//Parallel query set (manage a series of sets that do not want to be intersected), with the functions of query and consolidation
class DisjointSetUnion {
int[] f;//Stores the parent node of each element
int[] rank;//Record the depth of the tree corresponding to each root node
int n;
public DisjointSetUnion(int n) {
this.n = n;
this.rank = new int[n];//Record the depth of the tree corresponding to each root node
this.f = new int[n];//Stores the parent node of each element
for (int i = 0; i < n; i++) {
this.rank[i] = 1;//The initial value is set to 1
this.f[i] = i;//Set the parent node as yourself at the beginning
}
}
//Compressed path query method, recursive implementation
//Access the parent node layer by layer until the root node (the flag of the root node is that the parent node is itself). To judge whether two elements belong to the same set, you only need to see whether their root nodes are the same
public int find(int x) {
return f[x] == x ? x : (f[x] = find(f[x]));
}
//Merge method
public boolean unionSet(int x, int y) {
int fx = find(x), fy = find(y);//Find the root node of the two nodes
if (fx == fy) {//The root nodes of the two nodes are the same without merging
return false;
}
if (rank[fx] < rank[fy]) {//The depth of the tree with fx as the root node is less than that of the tree with fy as the root node
f[fx] = fy;
} else if (rank[fx] > rank[fy]) {
f[fy] = fx;
} else {
f[fx] = fy;
rank[fy] += 1;
}
return true;
}
}
//Edge class
class Edge {
//len is the distance between two points x and y
int len, x, y;
public Edge(int len, int x, int y) {
this.len = len;
this.x = x;
this.y = y;
}
}
2.6 1631. Minimum physical exertion path
You are going to take part in an outing. Give you a two-dimensional map of rows x columns, where heights [row] [column] represents the height of the grid (row, column). At first, you are in the top left grid (0, 0), and you want to go to the bottom right grid (rows-1, columns-1) (note that the subscript starts from 0). You can move up, down, left and right every time. You want to find a path that consumes the least energy.
The physical strength consumed by a path is determined by the maximum absolute value of the height difference between adjacent grids on the path.
Please return to the minimum physical exertion value from the upper left corner to the lower right corner.
rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 106
class Solution {
public int minimumEffortPath(int[][] heights) {
int m = heights.length;
int n = heights[0].length;
// Mapping
// The values in the array are {the number of the top / left node of the current node, the number of the current node, and the weight}
List<int[]> edges = new ArrayList<>();
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
int id = i * n + j;//Number each point
if (i > 0) {
edges.add(new int[]{id-n, id, Math.abs(heights[i][j] - heights[i-1][j])});
}
if (j > 0) {
edges.add(new int[]{id-1, id, Math.abs(heights[i][j] - heights[i][j-1])});
}
}
}
//Sort according to the weight from small to large
Collections.sort(edges, (edge1,edge2) -> edge1[2] - edge2[2]);
DisjointSetUnion dis = new DisjointSetUnion(m*n);
int ans= 0;//Record the minimum physical exertion value
for (int[] edge : edges) {
int x = edge[0];
int y = edge[1];
int v = edge[2];
dis.unionSet(x,y);
// When an edge with a weight of v is added, if the upper left corner and lower right corner change from non connected state to connected state, then v is the answer
if(dis.connected(0,m*n-1)){
ans = v;
break;
}
}
return ans;
}
}
// Joint search set
class DisjointSetUnion {
int[] f;
int[] rank;
int n;
public DisjointSetUnion(int n) {
this.n = n;
f = new int[n];
rank = new int[n];
for (int i = 0; i < n; ++i) {
f[i] = i;
rank[i] = 1;
}
}
public int find(int x) {
return f[x] == x ? x : (f[x] = find(f[x]));
}
public boolean unionSet(int x,int y) {
int fx = find(x);
int fy = find(y);
if(fx == fy) return false;
if (rank[fx] < rank[fy]) {
f[fx] = fy;
} else if (rank[fx] > rank[fy]) {
f[fy] = fx;
} else {
f[fx] = fy;
rank[fy] += 1;
}
return true;
}
// Judge whether the two points are connected
public boolean connected (int x,int y) {
x = find(x);
y = find(y);
return x == y;
}
}