brief introduction

Divide and conquer algorithm design idea

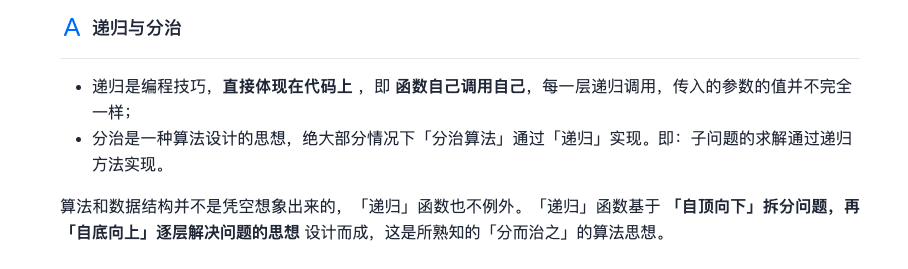
Recursion and divide and conquer

Design idea of recursive function: divide and rule (reduce and rule)

Top down problem solving

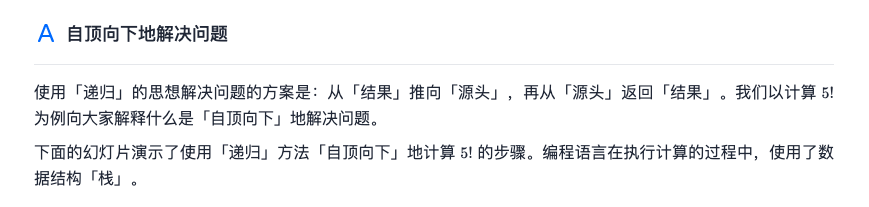
Why use stacks?

This step was also understood when I looked at the sword finger offer.

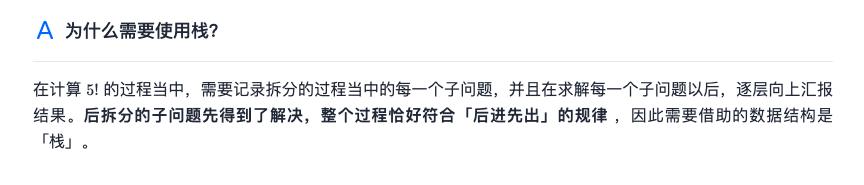
"Go out first" when splitting, and "come back" when merging

summary

Top down and bottom up

Comparison of factorial functions implemented using recursion and loop

We implement a function that inputs N and outputs the factorial of n. In order to simplify the description, we do not consider the case where the input is a negative integer and the output has integer overflow. That is, we assume that the input is legal and the integer of the result of factorial calculation is within the range of 32-bit integer.

public int factorial(int n) {
    if (n == 1) {
        return 1;
    }
    return n * factorial(n - 1);
}

Note: after the recursive method call returns, you can do something else. Take the above code as an example: after the return of factorial(n - 1), we will multiply the returned result value by n. The above code is equivalent to the following code:

public int factorial(int n) {
    if (n == 1) {
        return 1;
    }
    int res = factorial(n - 1);
    // Here, you can also perform an operation to realize the logic of "merger" in the "divide and conquer thought"
    return n * res;
}

This "being able to do something when the recursive call returns" corresponds to the process of "merging" in step 3 of "divide and conquer thought". "After the" recursive "call of the upper layer, we can implement some logic", which is easy to be ignored in the process of learning recursion. We should pay attention to the understanding of this detail in order to better understand and apply recursion.

/**
  * @param n
  * @param res Because the result of the upper layer of the recursive function is factorial, it needs to pass in 1 at the beginning
  * @return
  */
public int factorial(int n, int res) {
    if (n == 1) {
        return res;
    }
    return factorial(n - 1, n * res);
}

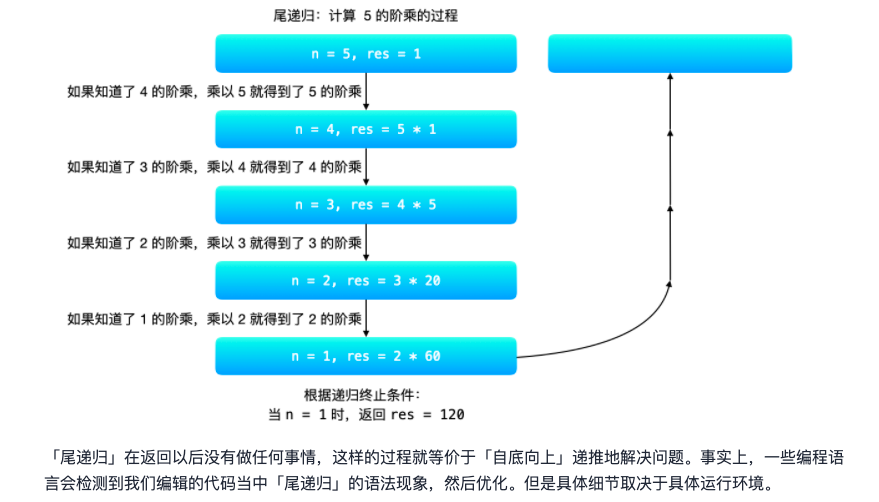
Use cycle calculation 5!
If we know the beginning of a problem, we can solve it step by step by recursion until we get the solution of the problem we want. Compared with recursion, this thinking direction is "bottom-up". Calculate 5! 5! We can also use loop implementation. The code is as follows:

public int factorial(int n) {
    int res = 1;
    for (int i = 2; i <= n; i++) {
        res *= i;
    }
    return res;
}

Friendly tip: if you have studied "dynamic programming", you will know that dynamic programming has two thinking directions: one is memory recursion, the other is recursion. Mnemonic recursion corresponds to the "top-down" problem-solving direction, and recursion corresponds to the "bottom-up" step-by-step problem-solving direction.

Obviously, the direction of "bottom-up" thinking directly starts from the "source" of a problem and gradually solves it. Compared with "top-down":

• The steps of splitting the problem layer by layer are missing;
• There is no need to record every sub problem in the splitting process with the help of a data structure (stack).

Recursion and recursion

Summary and Practice

"Top-down" and "bottom-up" respectively correspond to our two thinking paths to solve problems:

Top down: directly face and solve problems;
Bottom up: starting from the initial appearance of this problem, it gradually evolves into the appearance of the problem we finally want to solve.

50. Pow(x, n)

My code doesn't use recursion.... However, I finally began to pay attention to the boundary problem and code robustness because I saw the sword finger offer yesterday. Now I look at my own code, which is much better than before:

def myPow(self, x: float, n: int) -> float:
        negative_flag = False
        if x == 0: return 0
        elif n == 0: return 1
        elif n < 0: negative_flag = True
        res = 1

        for _ in range(abs(n)):
            res *= x
        
        if negative_flag: return 1 / res
        else: return res

It's too late to get there

Recursion is written, which is also difficult for large numbers:

def myPow(self, x: float, n: int) -> float:
        negative_flag = False
        if x == 0: return 0
        elif n == 0: return 1
        elif n < 0: negative_flag = True
        if n == 1: return x
        if negative_flag: return 1 / (x * self.myPow(x, abs(n)-1))
        else: return x * self.myPow(x, n-1)

Here are the answers:

According to the idea of the answer, I write fast power ➕ Recursion, or not too large:

def myPow(self, x: float, n: int) -> float:
        neg_flag = False
        if x == 0: return 0
        elif n == 0: return 1
        elif n < 0: neg_flag = True
        
        if n % 2 != 0: 
            if neg_flag: return 1 / (self.myPow(x, abs(n)//2)**2 * x)
            else: return self.myPow(x, n//2)**2 * x
        else: 
            if neg_flag: return 1 / (self.myPow(x, abs(n)/2)**2)
            else: return self.myPow(x, n/2)**2

Note that y*y instead of y**2 can be too large. I don't know why

class Solution:
    def myPow(self, x: float, n: int) -> float:
        def quickMul(N):
            if N == 0:
                return 1.0
            y = quickMul(N // 2)
            return y * y if N % 2 == 0 else y * y * x
        
        return quickMul(n) if n >= 0 else 1.0 / quickMul(-n)

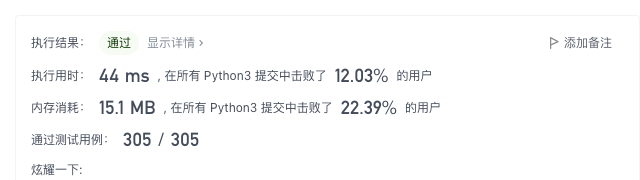
Sword finger Offer 65 No addition, subtraction, multiplication and division

I've done it before and reviewed it. I know how to use bit operation, but I still can't write it.
Look at the answer directly, which shows that my efficiency is not high. Although I brush the question, I still can't write it after I brush it and review it. I may be a pig. Only things processed by one's own brain will be remembered. Other people's ideas will never be copied directly.



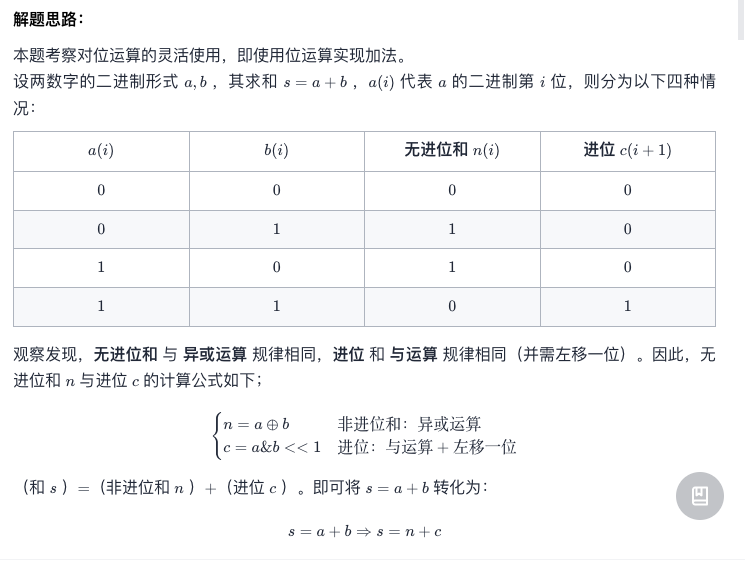
The following is the code you try to write according to the idea of the boss:

def add(self, a: int, b: int) -> int:
        n = a ^ b
        y = a & b << 1
        return n + y

Here's the big guy's code:

def add(self, a: int, b: int) -> int:
        x = 0xffffffff
        a, b = a & x, b & x
        while b != 0:
            a, b = (a ^ b), (a & b) << 1 & x
        return a if a <= 0x7fffffff else ~(a ^ x)

Recursion:

class Solution:
    def add(self, a: int, b: int) -> int:
        if b == 0: return a 
        return add(a ^ b, (a & b) << 1 )

Interview question 08.05 Recursive multiplication

Recursion. After reading the beauty of programming, I found that my thinking began to change. I began to try to think about the answers myself, and I should be confident that I can write the answers. If I swallow them now, those questions will treat us in the same way in the written examination or interview. As Inamori Kazuo said: do each problem in awe, figure out the ideas of each problem, and then do it. And began to pay attention to boundary conditions and robustness.

def multiply(self, A: int, B: int) -> int:
        if A <= 0 or B <= 0: return -1
        if B == 1: return A
        return A + self.multiply(A, B-1)

You can read books. Recursive calls are function calls. Each time a function is called, the computer will open up additional memory space for functions and parameters, so the occupied space will be relatively large. Equivalent to stack: last in, first out.