Monotonous stack

Monotone: therefore, the data stored in the monotone stack should be orderly, so the monotone stack is also divided into monotone increasing stack and monotone decreasing stack.

• Monotonically increasing stack: monotonically increasing stack is from the bottom of the stack to the top of the stack, and the data is from large to small
• Monotonic decrement stack: monotonic decrement stack is from the bottom of the stack to the top of the stack, and the data is from small to large

Pseudo code:

stack<int> st;
//Here, you generally need to add an end flag to the end of the array, which will be explained in detail in the following examples
for (Traverse this array)
{
	if (Stack empty || Stack top element is greater than or equal to the current comparison element)
	{
		Push ;
	}
	else
	{
		while (Stack is not empty && The stack top element is smaller than the current element)
		{
			Stack top element out of stack;
			Update results;
		}
		Current data stack;
	}
}

Classic examples

Leetcode.84 largest rectangle in histogram

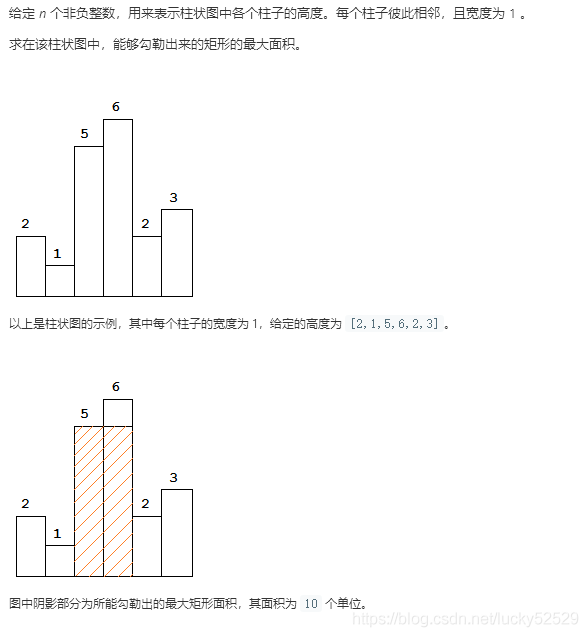
analysis

For the current column, the height is the benchmark, so we need to expand its width. We find the last column > = its height from left to right, and add it to the width (because it can expand the width for columns higher than it). Finally, update the maximum value.

BF

Violence (timeout)

public class Solution {

    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        // Special judgment
        if (len == 0) {
            return 0;
        }

        int res = 0;
        for (int i = 0; i < len; i++) {

            // Find the last subscript on the left greater than or equal to heights[i]
            int left = i;
            int curHeight = heights[i];
            while (left > 0 && heights[left - 1] >= curHeight) {
                left--;
            }

            // Find the last index on the right that is greater than or equal to heights[i]
            int right = i;
            while (right < len - 1 && heights[right + 1] >= curHeight) {
                right++;
            }

            int width = right - left + 1;
            res = Math.max(res, width * curHeight);
        }
        return res;
    }
}

Monotonous stack

• Set a monotonically increasing stack (0~n in the stack is monotonically increasing)
• Why use single stack?
• When a column meets a column higher than it, it can expand its height to the right
• When a column encounters a column lower than it, the low column affects its expansion, and we begin to update the data, because it is possible that the maximum area will appear in the sequence in the stack.

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] a = new int[heights.length+1];
        for (int i = 0; i < heights.length; i++) {
            a[i] = heights[i];
        }
        a[heights.length] = 0;  // In order to get all the elements in the stack out of the stack, the element 0 is added at the end

        int max = 0, p = -1;  // Maximum, stack top pointer
        Stack<Integer> stack = new Stack<>();
        int top = 0;
        for (int i = 0; i < a.length; i++) {
            if (stack.isEmpty() || a[stack.peek()] <= a[i]) {
                stack.push(i);
            } else {
                while (!stack.isEmpty() && a[stack.peek()] > a[i]) {
                    top = stack.pop();
                    // i-top: refers to the width of the current matrix, and height[top]: refers to the current height
                    // Again, emphasize monotonic increment in the stack
                    max = Math.max(max, (i-top)*a[top]);
                }
                stack.push(top);
                a[top] = a[i];
            }
        }
        return max;
    }
}

In particular, we should think about:

stack.push(top);
a[top] = a[i];

Note that when the element at the top of the stack is larger than the element to be inserted, the element at the top of the stack needs to be pop(), but the element to be inserted can be expanded to the left

However, in order to maintain the incremental attribute in the stack and allow i to expand to the left, we simply modified the subscript of i and changed it to the leftmost top subscript. Therefore, when we need to obtain the rectangular area based on him next time, the width will be expanded.

Blog reference Link

Monotone stack 2

The second solution: handwritten monotone stack, and use an array to record the width of the current column

Reference code: Source: Advanced Guide to algorithm competition

class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] a = new int[heights.length+1];
        for (int i = 0; i < heights.length; i++) {
            a[i] = heights[i];
        }
        // Define stack
        int[] s = new int[a.length+1];
        // Defines the width of the current histogram
        int[] w = new int[a.length+1];
        int max = 0, p = 0;  // Maximum, stack top pointer
        for (int i = 0; i < a.length; i++) {
            // When the top element of the stack is smaller than the current element, it is directly put on the stack
            if (s[p] < a[i]) {
                s[++p] = a[i];
                // Initial width 1
                w[p] = 1;
            } else {
                // The width value of the current left extension
                int width = 0;
                // When the stack top element is larger than the current element, the stack top element must not extend to the right
                // Pop to the stack top element is less than or equal to the current element, and the area of the stack top element of the monotonic stack is recorded in the pop process
                while (s[p] > a[i]) {
                    width += w[p];  // The width of the stack top element extending to the left
                    max = Math.max(max, s[p]*width);  // Update results
                    p--;  // pop() operation
                }
                s[++p] = a[i];  // Stack current element
                w[p] = width+1;  // The distance that the current element can be extended to the left. Because those just pop ped out are higher than the current element, the current element can be extended to the left
            }
        }
        return max;
    }
}

thank

strive

This afternoon is the "13th ICPC provincial competition". I'm still very excited to compete with the leaders of the whole province.

come on.